Обзор способов расчета энергетических
Т.е. написать параграф, в котором будут описаны техники моделирования, предполагающие
получение результатов с разными уровнями детализации:
моделирование систем с постоянными источниками,
не учитывающее переходных и волновых процессов.
моделирование систем с источниками периодических сигналов,
не учитывающее переходных и волновых процессов.
моделирование систем с источниками непериодических сигналов,
не учитывающее переходных и волновых процессов.
моделирование систем с источниками непериодических сигналов,
учитывающее переходные процессы и не учитывающее волновые.
моделирование систем с источниками непериодических сигналов,
учитывающее переходные и волновые процессы.
Оценка быстродействия САР
Оценить быстродействие можно по частотным характеристикам замкнутой и разомкнутой системы, используя:
|F(jw)| - АЧХ замкнутой системы
P(w) = Re(F(jw)) - вещественную ЧХ
W (jw) - АФХ разомкнутой системы
ЛАЧХ & ЛФЧХ
...
При этом в качестве критериев используют величины:
wр - резонансная частота, соответствует пику АЧХ, близка к частоте колебаний в переходном процессе;
wср - частота среза, соответствующая условию |W(jwср)|=A(wср)=1
или L(wср)=0 (по ЛАЧХ).
wп - частота соответствующая полосе пропускания замкнутой системы F(jw), определяемая из условия A(wп)=0,707.
wэ - эквивалентная полоса пропускания замкнутой системы: wэ = oҐ т |F(jw)|2 dw, - эта величина связана с вопросом пропускания системой помех. Кроме того, если ее рассчитать, включая отрицательные частоты, причем в герцах, то она совпадет с квадратичной ИТ-оценкой I'.
Оценка качества регулирования
Качество любой системы регулирования определяется величиной ошибки:
x(t) = g(t) - y(t) = Fx(p) g(t)
Но функцию ошибки x(t) для любого момента времени трудно определить, поскольку она описывается с помощью ДУ системы -
Fx(p) - высокого порядка, и зависит от большого количества параметров системы. Поэтому оценивают качество САР по некоторым ее свойствам, определяют которые с помощью критериев качества.
Критериев качества регулирования много. Их разделяют на 4 группы:
Критерии точности - используют величину ошибки в различных типовых режимах.
Критерии величины запаса устойчивости - оценивают удаленность САР от границы устойчивости.
Критерии быстродействия - оценивают быстроту реагирования САР на появление задающего и возмущающего воздействий.
Интегральные критерии - оценивают обобщенные свойства САР: точность, запас устойчивости, быстродействие.
Существует два основных подхода к оценке качества:
Первый использует информацию о временных параметрах системы: h(t), w(t); расположение полюсов и нулей ПФ замкнутой системы F(s).
Второй использует информацию о некоторых частотных свойствах системы: полоса пропускания; относительная высота резонансного пика; и т.д.
Оценка точности САР по воспроизведению гармонического сигнала
Если: g(t) = Gmsin(wkt), то амплитуда Xm = |Fx(jwk)| Gm = Gm / |1+W(jwk)|.
Поскольку Xm должна быть << Gm, то W(jwk) >> 1, следовательно Xm » Gm / |W(jwk)|.
Те, чтобы система воспроизводила сигнал с ошибкой, непревышающей Xm, ЛАЧХ системы должна проходить не ниже контрольной точки Ak с координатами: w = wk, L(wk) = 20lg |W(jwk)| = 20lg Gm/Xm.
Оценка запаса устойчивости


По виду АФХ разомкнутой системы оценивают запас устойчивости:
по амплитуде - L1=20lgb1
и L2=20lgb2
по фазе m1=180+j1
где: j1 - запаздывание по фазе на частоте единичного усиления при |W(jw)|=A(w)=1
или L(w)=0 (по ЛАЧХ).
Для абсолютно устойчивых систем (n<3) имеет смысл только величина L1, т.к. L2®Ґ. Для хорошо демпфированных систем bО[2...10), т.е. [6...20) дБ.
Запас устойчивости тем больше, чем больше b
и m1. Используя b
и m1 можно задать запретную область для АФХ. Но недостаток заключен в том, что если АФХ будет касаться запретной области в разных точках, перерегулирование s будет разным.



равный максимальному значению АЧХ замкнутой системы приведенной к коэффициенту усиления в области низких частот. Т.е. вынужденное движение на резонансной частоте будет иметь амплитуду в M раз большую, чем в области низких частот. И чем больше M, тем меньше запас устойчивости.
Если имеется только АФХ разомкнутой системы W(jw), то показатель колебательности M удобно использовать в виде фоновой сетки, которой можно пользоваться как линиями уровня M О [1/4; 1/2; 1; 0,707; 1,41; 2; 4]. Выполним расчет сетки:

где: (1) - уравнение окружности с радиусом R, и центром в точке C.
Оценка запаса устойчивости и быстродействия по переходной характеристике


s = (ymax - yҐ) / yҐ100, [%]
| Варианты s | 0 % | 10..30 % | 50..70 % | |
| Применяемость | редко | часто | избегают | |
| Запас по фазе | 900 | 600..300 | 300..100 | |
| Число колебаний | 0 | 1, 2 | 3, 4, ... |

D О 5; 2,5; 1,5; 1; 0,5; ... [%] от yҐ
, - установлено ГОСТ-ами.
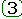
можно оценить по частоте колебаний переходной функции.

Время нарастания ограничено:
tн min - допустимым ускорением координат и предельными колебательными режимами;
tн max - требуемым быстродействием.
На рис. tз - максимальное допустимое время запаздывания (распространения) сигнала.
Определение типа границы устойчивости по виду годографа Михайлова

Астатизм первого порядка - "апериодическая" граница устойчивости.
Астатизм второго порядка - "апериодическая" граница устойчивости.
"Колебательная" граница устойчивости.
Граница устойчивости типа "бесконечный корень".
Определение устойчивости по логарифмическим частотным характеристикам
Рабочие файлы: [fr_ABCD.mcd]
Для определения устойчивости по критерию Найквиста можно строить не АФХ, а ЛАЧХ& ЛФЧХ разомкнутой системы.
Чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы сдвиг фазы на частоте единичного усиления разомкнутой системы W(jw)
не достигал значения -1800.
Если система условно устойчивая, то при модулях больших единицы, фазовый сдвиг может достигать значения -1800 четное число раз.
Определение устойчивости по М.Я. Ляпунову
Невозмущенное движение (при DxiҐ=0) называется устойчивым по отношению к пременным xi, если при всяком заданном положительном числе A2, как бы мало оно нибыло, можно выбрать другое положительное число l2(A2) так, что для всех возмущений Dxi0, удовлетворяющих условию:

возмущенное движение будет для времени t і T удовлетворять неравенству:

где: mi - коэффициенты, уравновешивающие размерности величин Dxi0.
Если с течением времени lim Dxi®0, то система ассимптотически устойчива.
Ошибка при движении по гармоническому закону g(t)=Gmsin(wkt)
Рассмотрим только первую составляющую ошибки:
x'уст = g(t) / [1+W (s)] = Xmsin(wkt+j)
где: g(t) - синусоида; [1+W (s)] - комплексное число.
Следовательно:
(1)
Xm = Gm / |1+W (jwk)| » Gm / A(wk).
Резюме:
Формула (1) позволяет идентифицировать положение неизвестной ЛАЧХ на данной частоте по амплитуде ошибки или сформулировать требования к ЛАЧХ при синтезе системы.
Особые точки ЛАЧХ определены комплексными сопряженными корнями. Поведение системы при данных частотах (wk=|jbk|) требует дополнительного исследования.
Особенность движения системы при гармоническом сигнале задания - это смена знака координат, которое во многих системах может сопровождаться нелинейными искажениями типа "ступенька" или сменой направления сил сухого трения.
Ошибки системы с астатизмом первого порядка
Если ПФ САР W(s) обладает астатизмом первого порядка, т.е. в области низких частот W(s)|s®0®Kv/s. Тогда первая составляющая ошибки:

т.е. в астатической системе первого порядка ошибка от задания равного константе равна нулю, ошибка от задания меняющегося с постоянной скоростью равна xv=v/Kv, а ошибка от задания меняющегося с постоянным ускорением нарастает до бесконечности.
Ошибки системы с астатизмом второго порядка
Если ПФ САР W(s) обладает астатизмом второго порядка, т.е. в области низких частот W(s)|s®0®Ke/s2. Тогда первая составляющая ошибки:

т.е. в астатической системе второго порядка ошибки от заданий равного константе и изменяющегося с постоянной скоростью равны нулю, а ошибка от задания меняющегося с постоянным ускорением равна константе xe=e/Ke.
Качество САР с астатизмом принято характеризовать величинами, называемыми добротностью по скорости и ускорению:

Ошибки статической системы
Здесь и далее будем рассматривать установившиеся составляющие ошибки системы в типовых режимах движения. Для чего будем анализировать уравнение ошибки:

где: g0+v/s+e/s2
- изображение представленного рядом Тейлора входного сигнала; s®0 соответствует установившемуся режиму.
Итак, если ПФ САР W(s) статическая, т.е. в области низких частот W(s)|s®0®K. Тогда первая составляющая ошибки:
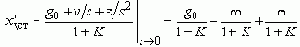
т.е. в статической системе ошибка, вызванная заданием равным константе, так же константа, но меньшая на величину 1+K, а ошибки от заданий меняющихся с постоянными скоростью или ускорением нарастают до бесконечности.
Основы моделирования систем
Введение в дисциплину
Проблематика, задачи и цель моделирования
Технологии функционирования моделирующих программ
Обзор и классификация моделирующих программ
Решатели моделирующих программ
Понятие о структурном и мультидоменном физическом моделировании
Идея мультидоменного физического моделирования
Понятие об управляемом событиями моделировании
Инструментарий моделирующих программ
Введение в технологию моделирования на основе направленных графов
Принцип поточного исполнения блок-схем (моделей)
Библиотеки блоков графических языков
Блоки обладающие эффектом памяти
Понятие о начальных условиях модели
Понятие о параметрах модели
Понятие о методах интегрирования
Выбор шага симуляции и метода интегрирования
Введение в технологию моделирования на основе ненаправленных графов
Принципы построения графа схемы физической принципиальной
Элементы ненаправленного графа
Пассивные элементы ненаправленного графа (потребители энергии)
Безинерционный элемент (активное сопротивление)
Реактивный элемент 1
Реактивный элемент 2
Активные элементы ненаправленного графа (источники энергии)
Источник движущей силы (генератор энергетических потенциалов)
Источник потока (генератор потока материи)
Прерыватель алгебраических петель (инициатор потока материи)
Заземлитель потенциала
Узлы ненаправленного графа
Распределяющий (материю) узел
Аккумулирующий (материю) узел
Рекомендации к использованию библиотеки элементов
Обзор методов анализа моделей, систем и сигналов
Идентификация моделей
Символьный анализ математического описания моделей
Билинейное преобразование
Разложение математического описания модели САР в степенной ряд
Частотный анализ моделей и систем
Вычислительные алгоритмы идентификации ЧХ моделей
Измерительные алгоритмы идентификации ЧХ моделей и систем
Алгоритмы идентификации ЧХ систем на основе технологий распознавания образов
Литература
Приложение 1. Архитектура моделирующих программ
Приложение 2. О структурном кризисе в методике преподавания блока дисциплин связанных с расчетом цепей преобразования энергий
myVisibility(ww=true);
Особенности линеаризованного уравнения
Оно является приближенным - отброшены члены высшего порядка малости.
Неизвестными функциями являются не полные величины, а их отклонения
D... от установившихся значений.
Уравнение является линейным относительно отклонений D..., при этом масштабирующие коэффициенты (частные производные) могут быть постоянными или переменными во времени.
Внешнее воздействие линеаризации не подлежит.
Ответы на часто задаваемые вопросы
Когда я нажимаю на ссылки около слов "Рабочие файлы" я вижу непонятный текст. Что мне делать?
На вашем компьютере не установлена студенческая версия программы VisSim. Ее надо скачать и установить на ваш компьютер. Часть рабочих файлов заархивированных в данном ресурсе являются рабочими файлами программы Electronics WorkBench 4.1. Она так же должна быть установлена на вашем компьютере.
| Пример "непонятного текста" | |
| ; VisSim Block Diagram Format (VBDF) ; Copyright ©1989-1999 Visual Solutions PA=1 POa="Nikolay Klinachyov" PV=3.000 PS=0 PE=0.5 PP=0.0001 PI=172 PX=0.0001 PN=1e-006 PL=5 PT=1e-005 Pn=-8,6,14,"MS Sans Serif" ... |
Откуда загрузить студенческую версию программы VisSim?
См. раздел "Download" сайта "VisSim в России".
Является ли студенческая версия программы VisSim бесплатной?
Да, студенческая версия программы VisSim распространяется бесплатно. По условиям правомочного использования программы вам нужно зарегистрироваться.
Я установил программу VisSim, но когда я нажимаю на ссылки, указывающие на рабочие файлы программы VisSim, распаковка файла блокируется и выдается сообщение о том, что файл не доступен. Что мне делать?
Есть подозрение, что причина в антивирусной программе (Касперского), которая толи сама блокирует их запуск, толи меняет настройки у браузера MSIE в реестре и последний сам не запускает файлы по гиперссылке. Как правило, деактивация антивирусного монитора не дает желаемого результата (запрет на загрузку сохраняется где-то в реестре). Деархивируйте файл tau_knv.chm и запускайте файлы обычным образом из директории ...\EXMPL\.
Команда деархивации: hh -decompile c:\DIR\ c:\DIR\tau_knv.chm
Подобная же ситуация наблюдается на тех компьютерах, где на новую версию браузера MSIE была установлена старая. Сделанного не вернуть - деинсталляция новой версии браузера не удаляет ряд COM-объектов. Старая версия их не переписывает, а пользоваться ими корректно не умеет. Рекомендуется вернуться к новой версии браузера MSIE.
Я обнаружил, что в студенческой версии программы VisSim нет документации. Где ее можно взять?
Переведенную на русский язык справку программы можно найти на сайте "VisSim в России", см. раздел "Download", файл vsmhlpru.zip.
У меня есть вопросы о моделировании в программе VisSim. Кому я могу их задать?
Вам рекомендуется вступить в дискуссионную группу "Симуляция движения (моделирование)". В данном учебно-методическом комплексе (см. навигацию) есть подробные инструкции о том, как работать с дискуссионной группой.
Отыскание ПФ системы с var-параметрами
ПФ системы с переменными параметрами можно определить либо по функциям веса:
W(s, t) = -Ґt т w(t-J, J) e-(t-J)s dJ
= o+Ґ т w(q, t-q) e-qs dq
,
либо по переходной функции h(t-J, J):
W(s, t) = s -Ґt т h(t-J, J) e-(t-J)s dJ
= s o+Ґ т h(q, t-q) e-qs dq
,
но этот подход нерационален, т.к. требует знания типовых реакций системы h и w.
Более удобно находить ПФ W(s, t) из исходного ДУ с var-параметрами:
A(s, t) W(s, t) + N{W(s, t)} = B(s, t) ,
где:
A(s, t) = a0(t)sn+...+an(t) ; B(s, t) = b0(t)sm+...+bm(t) ;
N{W(s, t)} =[ dA/ds dW/dt + ... + 1/n! dnA/dsn dnW/dtn
] .
Решение ДУ, т.е. ПФ W(s, t) будем искать в виде ряда:
W(s, t) = W0(s, t) + W1(s, t) + ...
где: W0(s, t) = B(s, t) / A(s, t); Wk(s, t) = N{Wk-1(s, t)} / A(s, t) .
Памятка по эксплуатации
Материала в теоретическом разделе не достаточно для освоения дисциплины. Его объём специально ограничен. Раскрытие сути отдельных аспектов теории входит в обязанность лектора. При самообучении студент должен дополнительно пользоваться учебниками.
Лектору, при появлении необходимости возвращения к прочитанному материалу, рекомендуется запускать копию пособия, и переключатся между окнами.
Для покадрового изучения рисунков с анимацией необходимо пользоваться кнопками "Стоп" и "Обновить" в инструментальной панели окна документа.
Рекомендуемое разрешение проекционной аппаратуры для визуализации на лекциях любого раздела документа - 800x600x256. Однако оформление документа не искажается и при видеорежиме 640x480x16.
При работе с графическим разрешением 640x480 рекомендуется скрыть панель оглавления, при этом сохраняется возможность навигации по документу посредствам гиперссылок.
При работе с проекционной аппаратурой, можно увеличить шрифт во всем документе. Закройте документ. Запустите браузер MSIE. Увеличьте шрифт по умолчанию с помощью кнопки в его инструментальной панели. Закройте браузер MSIE. Вернитесь к документу. При необходимости более существенного изменения оформления документа составьте свою каскадную таблицу стилей и подключите ее к браузеру MSIE (Сервис > Свойства обозревателя > Общие > Оформление).
Замечено, что некоторые антивирусные программы-мониторы блокируют распаковку рабочих файлов моделирующих программам из данного пособия. Измените их соответствующие настройки. Пособие распространяется с электронной подписью сделанной автором (tau_knv.chm.sig - подпись, KNV.asc - публичный ключ КлиначёваН.В.). Используя программу PGP, вы можете убедиться, что при распространении данный файл ни кем не был изменен.
Параметры цифровых фильтров
1/dT = sampleRate
Частота дискретизации фильтра. Определяется как обратная величина от периода времени dT, через который цифровая вычислительная машина способна выполнять подпрограмму, рассчитывающую соответствующее разностное уравнение (4)
Частота (frequency)
В зависимости от типа фильтра - это "частота сопряжения" (оценивается по пересечению ЛАЧХ с уровнем -3 дБ), "резонансная частота" для полосового и режекторного фильтров, "центральная частота" полософормирующего фильтра, или "центральна частота наклонного участка" фильтра-ступени (фильтра-горки)
К в полосе (dBgain)
Коэффициент передачи на модифицируемом участке ЛАЧХ для полософормирующего фильтра и фильтра-ступени
Добротность (Q)
Отношение резонансной частоты фильтра к ширине его полосы. В зависимости от типа фильтра при формировании требований к ЧХ, бывает удобней пользоваться эквивалентными параметрами - "полосой" и "наклоном"
Полоса (bandwidth)
Ширина полосы рабочих частот фильтра. Для полосового и режекторного фильтров оценивается по пересечению их ЛАЧХ с уровнем -3 дБ. Для полософормирующего фильтра - по пересечению их ЛАЧХ с её средним уровнем (dBgain/2). Для фильтра-ступени - это длина наклонного участка
Наклон (shelf slope)
Модуль наклона ЛАЧХ фильтра-ступени. Максимально возможный наклон (без появления колебательности ЛАЧХ) равен 1 Белу за октаву. При задании малого значения наклона фильтр-ступень превращается в фильтр-лестницу (ЛАЧХ похожа на две ступеньки). Наклонный участок становится нелинейным
Пассивные элементы ненаправленного графа (потребителиэнергии)
В каждом из энергетических доменов существует от одного до трех (известных) простейших физических устройств, которые называются электрическим, магнитным, тепловым, гидравлическим, акустическим, механическим, ротационным и др. сопротивлениями. Таким образом, чуть округлив, можно сказать, что для названных энергетических доменов закон Ома имеет 21 формулировку. Формулы закона Ома записываются тремя способами:

Три формы записи закона Ома определяют три формальных примитива, которые являются пассивными элементами ненаправленного графа, т.е. моделями потребителей энергии.
Определимся так же с тем, что все элементы ненаправленного графа будут асимметричными, т.е. с тем, что именно поток материи по элементам будет определять разность энергетических потенциалов на их выводах, а не наоборот.
Перечень лабораторных занятий по дисциплине "Теория систем автоматического регулирования"
| ЧАСТЬ 1
1. Знакомство с моделирующим ПО 2. Типовые динамические звенья 3. Принципы и законы регули-вания 4. Анализ устойчивости САР 5. Оценка качества регулирования 6. Повышение точности САР 7. Коррекция САР 8. Синтез САР ЧАСТЬ 2 09. САР с var-параметрами 10. Системы с запаздванием 11. Импульсные системы 12. Цифровые системы 13. Релейные системы Справочный материал |
Передаточные функции САР
Передаточная функция
Функция, связывающая один входной и один выходной сигналы САР. Является формой записи системы ДУ САР решённой относительно требуемой выходной координаты. Обычно ПФ записывается не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.
ПФ-ии получают из ДУ решенного относительно требуемой координаты системы (уравнение (4) или (5)). Для чего правую часть уравнения делят на характеристический полином D(p). Отношения полиномов в правой части при возмущающих воздействиях и есть ПФ-ии.

Для типовой структурной схемы замкнутой САР различают 3 основные ПФ, применяемые для исследований:
W(p) = y(t)/x(t) Ч Wос(p) = Wрег(p) Wо(p) Wос(p) - ПФ разомкнутой системы;
F(p) = y(t)/g(t) - ПФ замкнутой системы;
Fx(p) = x(t)/g(t) - ПФ замкнутой системы по ошибке.
Запишем по структурной схеме уравнение движения для разомкнутой системы:

где: Wпрк(p) - ПФ прямого канала системы.
Замкнем систему с помощью уравнения замыкания:

Тогда совместное решение даст уравнение движения замкнутой системы:

и уравнение ошибки замкнутой системы:

При отсутствии помехи f (t) выходная величина связана с задающим воздействием ПФ замкнутой системы:

А ошибка - с задающим воздействием ПФ замкнутой системы по ошибке:
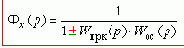
При этом:
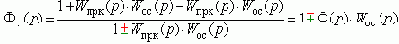
ПФ для возмущений

Поскольку для произведения 2х операторных многочленов: F(s)
(изображение возмущения) и W2(s) нельзя найти Z-преобразование раздельно, см. правило 2, то ПФ по возмущению удобно определять для эквивалентных возмущений F1(z), приведенных к входу ИЭ:

ПФ системы с экстраполятором, осуществляющим АМ первого или второго рода

Найдем изображение Лапласа для частично заполненного импульса:

Тогда Z-изображение экстраполятора и непрерывной части:

где: e= 1 - g ; W(z) не учитывает коэффициент передачи ИИЭ равный 1/T.
Если g << 1, то e -gTs » 1 - gTs, тогда:

К этой формуле, в первом приближении, сводится и АМ второго рода.
ПФ системы с экстраполятором нулевого порядка и звеном запаздывания

Экстраполятором нулевого порядка являются: 1) УВХ и 2) ЦАП.
Найдем изображение Лапласа для единичного импульса:

Тогда Z-изображение экстраполятора и непрерывной части со звеном запаздывания:

где: e = 1 - t/T
; 0 < t < T ; W(z) не учитывает коэффициент передачи ИИЭ равный 1/T.
ПФ замкнутой импульсной системы

Опишем систему в изображениях Лапласа:
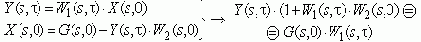

те.:

ПФ по ошибке Fx может быть получена решением системы относительно ошибки x.
Поскольку запаздывание не определяет свойства системы в области низких частот, практически всегда для оценки качества могут быть использованы формулы

(осталась особенность - "W1W2(z)", см. правило 2 преобразования структурных схем)
ПФ звена чистого запаздывания

при 0 < t < t.
Разложим правую часть уравнения (т.е. выходной сигнал) в ряд Тейлора:

или

т.е.:
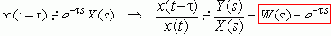
ПЛАН РАЗВИТИЯ ДАННОГО РУКОВОДСТВА
Разработка лабораторных работ для второго семестра (нелинейные и цифровые системы) (к февралю 2001г.).
Дальнейшая взаимная интеграция моделей из разных моделирующих пакетов. Организация одновременной работы моделей (в разных пакетах) в динамическом режиме посредствам технологий динамического обмена данными (DDE - dinamic data exchange, на базе ActiveX). Пример: регулятор в пакете Electronics Workbench, объект в пакете VisSim, - должны работать совместно.
Разработка моделей, предполагающих наличие в контуре модели реального технического устройства, подключенного посредством платы сбора данных - (DAQ-board).
Подготовка моделей для альтернативных моделирующих пакетов, например "МВТУ" (если будет договоренность с разработчиками).
30.10.2000
Сделать "D-разбиение" по вариантам см. задачник.
| 1. Цель работы | 2. Предварительное домашнее задание | 3. Содержание работы |
| 4. Обработка результатов | 5. Методические указания к моделированию и рекомендации к содержанию отчета | 6. Контрольные вопросы |
Работа 4
3.7. Провести исследование устойчивости модели электронного усилителя на трехкаскадном ОУ (файлы ou3.vsm и ou2+1.ca4)
3.8. Исследовать влияние контурного коэффициента усиления на полосу пропускания замкнутой системы на примере электронного усилителя на ОУ.
Работа 5?[err_pid.vsm] [PIDTUNE.vsm]
Выяснение сути корневых методов оценки качества.
Работа 6?[ASTATIC.vsm]
Изучение основных методов повышения точности САР: 1) увеличение коэффициента усиления разомкнутой цепи, 2) применение регулирования по производным от ошибки с увеличением контурного коэффициента усиления, 3) повышение степени астатизма, 4) применение неединичных обратных связей или масштабирующих устройств на входе / выходе и 5) комбинированного управления.
4.3. Выполнить количественное исследование результатов применения методов повышения точности САР на основе исследований (измерений) ошибки x(t). По необходимости рекомендуется использовать тест-сигналы задания g(t): единичную ступенчатую функцию 1(t), синусоидальный, меняющийся с постоянной скоростью или ускорением (см.
сигнал g(t) в файле err_ast3.vsm). Для измерений ошибки рекомендуется использовать: датчики скорости и ускорения (дифференцирующие звенья), преобразователи построенные в соответствии с интегральными оценками качества, а так же измерители действующего или средневыпрямленного значений. Выбор схемы измерения ошибки x(t) следует обосновать.
3.6. Определить первые коэффициенты ошибок систем до и после применения методов повышения точности.
(можно измерить первые коэффициенты ошибок систем до и после повышения точности).
4.1. Один из методов повышения точности САР - это повышение степени астатизма. Метод реализуется применением либо интегрирующего, либо изодромного звена включаемого в разрыв контура регулирования. Качественно описать результаты применения упомянутых технических решений (в сравнении). Сформулировать достоинства, недостатки (ограничения в применении). Привести поясняющие графические зависимости (информацию удобно представить в режиме пререкрытия графиков).
Работа 8 [Ak_wk.vsm] [wo.vsm]
Среди предложенных моделей идентифицировать устойчивые в разомкнутом состоянии.
3.2. Для неустойчивых в разомкнутом состоянии систем спроектировать последовательные компенсационные звенья.
Понятие о характеристическом уравнении
Было сказано, что устойчивость системы связана с природой самой системы, а не с тем, как внешние источники движущих сил (задание, помехи) заставляют перемещаться ее координаты. Очевидно, что невозможно описать цепь преобразования энергии (систему) не учитывая источников. Поэтому в правой части ДУ описывающих систему всегда будут присутствовать источники движущих сил (вспомните как записываются уравнения по II закону Кирхгофа). Однако если их обнулить, то система ДУ не потеряет смысла. После отключения источников в любой линейной цепи преобразования энергии возникнет переходный процесс обусловленный энергией, которую накопили пассивные реактивные элементы цепи (собственный переходный процесс). Именно он определит, будет ли система устойчивой. И именно эта система ДУ, в которой обнулены величины источников движущих сил, называется характеристической. Если система характеристических ДУ решена относительно одной из координат, то она называется характеристическим уравнением.
Понятие о методах интегрирования
Рабочие файлы: [Интеграторы]
На компьютерах, дискретных по своей природе, реализовать интегратор, лишенный методических погрешностей невозможно. Существует группа классических подпрограмм (функций), которые реализуют операцию интегрирования. В простейшем случае математическая функция, закрепленная за всеми интеграторами модели, имеет вид: y [n] = y [n-1] + x [n], - где: x [n] - входной аргумент, y [n] - возвращаемое значение. Погрешности у этих подпрограмм в конкретных ситуациях проявляются по-разному, поэтому все программы математического моделирования в своих настройках содержат переключатель методов интегрирования. Обычно в список входят следующие методы:
Эйлера (с запаздыванием)
Трапециидальный
Рунге-Кутта 2-ого порядка
Рунге-Кутта 4-ого порядка
Адаптивный Рунге-Кутта 5-ого порядка
Адаптивный Булирша-Стоера
Эйлера (с упреждением)
На рисунке для справки представлены блок-схемы, передаточные функции и частотные характеристики основных дискретных квазианалогов интеграторов. Особенность блок-схем интеграторов построенных согласно методам Эйлера с упреждением и трапеций состоит в том, что их пропорциональный канал разорван с помощью неявного решателя. В противном случае их нельзя было бы использовать в блок-схемах с обратными связями.

Понятие о начальных условиях модели (Initial Condition)
Рабочие файлы: [Начальные условия / Параметры & h(t)]
Начальные условия
Значения физических величин первого или второго рода (чье произведение всегда есть мощность) характеризующие динамическое состояние процесса преобразования энергии в системе в интересующий момент времени (обычно это начало функционирования). При моделировании систем начальные условия задаются в силу существования законов коммутации для реактивных по своей природе физических устройств, т.к. их энергетическое состояние не может измениться мгновенно. Начальным условием может быть либо величина потока материи (электрической, магнитной, тепловой, гидравлической, механической, акустической или ротационной) в L-сопротивлении, либо разность энергетических потенциалов (соответствующей природы) на выводах C-сопротивления.
Если рассматривать первый шаг симуляции (n=0), то из сотен библиотечных блоков только те, что обладают эффектом памяти, могут иметь на своих выходах ненулевые значения y[-1]. Эти значения как раз таки и являются начальными условиями и устанавливаются вручную для блоков 1/S и 1/Z (а так же для тех, что построены на их основе).
Реальные системы начинают функционировать при самых разных начальных условиях. Повторное включение электрической схемы, в которой конденсаторы не разрядились полностью. Самовозбуждение машины постоянного тока от остаточного магнитного потока такой-то величины. Охлаждение утюга до комнатной температуры от нагретого до такой-то температуры состояния. Самостоятельный разгон ракеты, которой начальную скорость придал несущий ее самолет. Функционирование логической схемы с элементами памяти (с триггерами) от предустановленного состояния и т.д.
Понятие о параметрах модели
Параметры модели
Физические величины, которые характеризуют модель независимо от ее текущего динамического состояния. К параметрам относятся: сопротивления1 (электрическое, магнитное, термальное, гидравлическое, механическое, акустическое, ротационное, и т.д.); отношения сопротивлений (коэффициенты передачи); меры инерционности (постоянные времени).
1)Если речь идет о сопротивлениях реактивного характера, то в качестве параметров могут выступать физические величины их определяющие (например, индуктивность катушки, емкость конденсатора, и т.д.).
Понятие о параметрической функции
Рабочие файлы: [Интеграл Дюамеля] [Интеграл свертки]
[Интеграл свертки]
Очевидно, что реакции САР с var-параметрами на стандартные возмущения 1(t) и d(t) будут зависеть от момента времени поступления сигналов. В связи с этим функцию веса можно изобразить в виде поверхности:


Нормальную весовую функцию w(t-J,J)
при J=const.
Сопряженную весовую функцию w(t-J, J)
при t=const.
Реверс-смещение сопряженной весовой функции w(q, t-q)
при t=const.
Заметим, что в системах с постоянными параметрами рельеф функций веса цилиндрический и нормальная функция веса совпадает с сопряженной (с реверс-смещением).
Если на систему, со свойственной ей функцией веса w(t-J, J), действует входной сигнал f(t), то элементарная реакция на выходе системы в произвольный момент времени t=J
будет:
dy = w(t-J, J) f(J) dJ
.
Полный сигнал определяется как суперпозиция элементарных реакций:
y = ot т w(t-J, J) f(J) dJ
.
А если использовать реверс смещение q = t-J
(t=const):
y = ot т w(q, t-q) f(t-q) dq
,
то получим интеграл свертки для квазистационарных систем.
Найти функцию веса для систем первого и второго порядков можно аналитически. Для систем высших порядков существуют численные методы.
Понятие о переходном процессе конечной длительности

Принципиальным недостатком линейных систем является тот факт, что любой переходный процесс будет иметь бесконечную длительность. Это объясняется тем, что при уменьшении значений сигналов на входах интеграторов пропорционально уменьшается скорость изменения их выходных координат. Т.е. если в линейной астатической системе ошибка становится меньше, то тут же понижается скорость ее компенсации по цепи ООС (см. рис., кадр 1).
Если же на некоторое время периодически замораживать сигнал в цепи ООС, то скорость изменения выходной координаты интегратора в течение периода "заморозки" уменьшаться не будет, а при правильном подборе периода "заморозки" можно добиться переходного процесса конечной длительности, завершающегося за один или же два цикла (см. рис., кадры 2 и 3).
Следует отметить, что подобная импульсная система на время "заморозки" сигнала ООС приобретает все достоинства и недостатки не имеющих ОС систем.
Пусть имеем характеристическое уравнение:
a0 s n + a1
s n-1 + ... + an-1 s + an
= 0 .
Приведем его к нормированному виду (разделим на an
и выполним подстановку
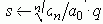
q n + a1/an
(W0 q) n-1 + ... + ak/an (W0
q) n-k +...+ 1 = 0 ,
где:

- среднегеометрический корень.

вызовет пропорциональное радиальное смещение корней. Т.е. вид переходного процесса меняться не будет, но будет меняться его временной масштаб. Поэтому среднегеометрический корень W0 является мерой быстродействия.
Для приведенного уравнения время будет безразмерным
t = W0 t, переходная функция h(t) в случае кратных вещественных корней или одной пары комплексных будет ограничена минорантой и мажорантой:

где: u(h, t) = e -ht [1 + (ht)1/1! + (ht)2/2! + ... + (ht)n-1/(n-1)! ]
- разложение в ряд Тейлора огибающей той составляющей в пререходном процессе, корень которой ближе к оси "+j".
На рис. демонстрируется, что любой переходный процесс в любой системе будет затухать тем медленней, чем больше корней вблизи оси "+j".
Понятие о структурном и мультидоменном физическом моделировании
Структурное моделирование
Техника моделирования основанная на использовании моделей в виде преобразующих сигналы блоков. Связи между входными и выходными сигналами устанавливаются посредством задания передаточных функций. Поскольку структурные блоки имеют выраженные входы и выходы, построенные согласно этой технике модели иногда называют направленными сигнальными графами (см. рис.1).
Мультидоменное физическое моделирование
Техника моделирования основанная на использовании универсальной библиотеки моделей элементов физических устройств, из которых можно составлять схемы физические принципиальные. Поскольку в энергетических цепях поток материи может менять направление, построенные согласно этой технике модели иногда называют ненаправленными или бинаправленными сигнальными графами (см. рис. 2).
Естественно-физическое моделирование
Переходная техника физического моделирования не использующая модели элементов физических устройств и предполагающая задание системы уравнений либо в графической, либо в текстовой форме (см. рис. 3).
Математический аппарат теории систем автоматического регулирования предполагает исключение алгебраических уравнений со свободными переменными из моделей технических устройств. Таким образом, техника структурного моделирования, использующая модели в форме передаточных функций, требует наличия лишь явного решателя. Явный решатель подключается ко всем интеграторам модели (блоки 1/S), и, с той или иной точностью (на что влияет выбор метода интегрирования), интегрирует соответствующие сигналы, обеспечивая тем самым решение дифференциальных уравнений.

Рис. 1
Неявный решатель позволяет перейти к иной технике построения моделей, которая предусматривает закрепление за группами уравнений условных графических обозначений элементов энергетических цепей (резистора, транзистора, магнитного сердечника, пневмоцилиндра и пр.).

Рис. 2
Следует отметить, что в программах с поточной моделью управления подключение неявного решателя возложено на пользователя. Задача составления моделей физических элементов, с такой структурой, дабы при составлении из них произвольных энергетических цепей корректно стыковались алгебраические уравнения, вызывала затруднения. По этой причине данный класс программ отстал в технике мультидоменного физического моделирования и в них распространена устаревающая техника естественно-физического моделирования.

Рис. 3
На рисунках, для сравнения, демонстрируются модели одной и той же электрической схемы построенные согласно описанным техникам.
Построение НЧ части желаемой ЛАЧХ



Ke > Ke
треб, но: затруднено демпфирование и увеличиваются ВЧ шум.
Kv > Kv треб, но: увеличиваются НЧ шум.
Истинная ЛАЧХ должна быть поднята на 3 дБ, для компенсации ослабления в 1,4142 раза в зоне частоты сопряжения.
Построение областей устойчивости - D-разбиение
Пусть имеем произвольную передаточную функцию систем:

и требуется оценить влияние разброса параметров на устойчивость.
Выделим два параметра (K и Ti), влияние которых на устойчивость следует оценить. Остальные параметры зафиксируем. Воспользуемся алгоритмом:

Итог итерационного алгоритма - область устойчивости (D-разбиение) ограниченная осями и графиком (уменьшение K и одной из постоянных времени объекта, как правило, положительно сказывается на устойчивости).
При заданной частоте существует только одна координата (K, Ti), которой будет соответствовать положение системы на границе устойчивости.
Наиболее удобно в итерационном алгоритме для системы любого порядка использовать критерий Михайлова, тогда уравнение границы:
D(jw) = 1+ W(jw) = 1 + R(jw)/Q(jw) = R(jw) + Q(jw) = 0,
т.е. K (1 + T3(jw)) ... + jw(1 + T1(jw)) (1+T2(jw)) ... = 0
Построение ВЧ части желаемой ЛАЧХ
Исходные данные: w0 иT1 - определены при построении НЧ части желаемой ЛАЧХ.

Задаются перерегулированием s и определяют M:
| s, % | 13,8 | 26,5 | 37,2 | 44,6 |
| M | 1,1 | 1,3 | 1,5 | 1,7 |
Зная M, определяют положение постоянной времени T2 (начало корректирующего участка):



Проверяют, чтобы резонансные пики высокочастотных колебательных звеньев не достигали вновь уровня 20lg M/(M+1).

1-2 или модификациям, путем уменьшения постоянных времени до значения:

Если это невозможно, то формируют участок -20 дБ/дек аналогично методике для систем с астатизмом 2-ого порядка.
Повышение точности САР
Задача повышения точности САР обычно предполагает существенный пересмотр ее структуры. Возможны замены или добавления отдельных звеньев в контуре.
Общими методами повышения точности САР являются:
Увеличение коэффициента усиления K разомкнутой цепи
Повышение порядка астатизма r
Применение регулирования по производным
Использование комбинированного управления
Введение неединичных обратных связей
Включение масштабирующих устройств на входе или выходе
Повышение точности систем применением регулирования по производным от ошибки
Использование регулирования по производным от ошибки, позволяет повысить точность системы, поскольку:
Система начнет чувствовать не просто наличие ошибки, но и тенденцию к ее изменению.
Повышается запас устойчивости по фазе и можно поднять общий коэффициент усиления.



Сравнивая полученные коэффициенты с исходными можно увидеть, что все, кроме c0, уменьшаются. При соответствующем выборе Td
можно обратить в ноль один из старших коэффициентов c1, или
c2, или ...
Последовательное включение 2х пропорционально-дифференцирующих элементов, позволяет обратить в ноль два старших коэффициента ошибки.
САР является инвариантной по отношению к задающему или возмущающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, ошибка системы не зависит от этого воздействия.
Повышение точности систем увеличением коэффициента усиления
Рассмотрим задачу повышения точности системы второго порядка, состоящей из 2х апериодических звеньев.



будет тем меньше, чем больше K.
Очевидно так же, что первые коэффициенты ошибок не будут равны нулю, но будут тем меньше, чем больше K:

Т.е. увеличение K уменьшает ошибки во всех типовых режимах.
Метод эффективен, широко применяется, но обычно увеличение K
приводит к уменьшению запаса устойчивости (см. ЛАЧХ & ЛФЧХ)
Повышение точности систем увеличением порядка астатизма
Повышение порядка астатизма используется для устранения установившихся ошибок в типовых режимах движения.




где: Kv = Ki K ;
Ke = Ki1 Ki2
K.
Очевидно, что последовательное включение уже 2-х интеграторов приведет к появлению структурной неустойчивости, когда ни при каком значении общего коэффициента усиления невозможно получить устойчивую систему.
Это затруднение можно преодолеть использованием изодромных устройств:



и не влиял на устойчивость системы.
Поскольку постоянные времени изодромных устройств Ti, обычно, самые большие в системе, то определенные ими составляющие в переходном процессе затухают наиболее медленно, ухудшая тем самым динамические свойства системы. Это видно и по необращенным в ноль коэффициентам ошибок, поскольку коэффициент усиления интегратора в изодромном устройстве Ki=1/Ti
обычно меньше единицы.
Правила построения асимптотических ЛАЧХ& ЛФЧХ
Правила построения асимптотических ЛАЧХ & ЛФЧХ, точнее каждого слагаемого выражения (2) показаны на рисунках.




Точность асимптотических ЛАЧХ & ЛФЧХ достаточна в большинстве случаев. Для звеньев первого порядка максимальная амплитудная ошибка вблизи частоты сопряжения составляет 3 дБ. Максимальная фазовая ошибка - 6%. Фрагмент ЧХ колебательного звена вблизи резонансной частоты лишь иногда следует уточнить по опорным справочным кривым для данного
z.
Правила преобразования структурных схем дискретных систем
Рабочие файлы: [series_z.vsm]
 Wп(s) = W1(s) + W2(s) W(z) = W1(z) + W2(z)  Wп(s) = W1(s) W2(s) W(z) = Z { W1(s) W2(s) } = W1W2(z) те. W(z) № W1(z) W2(z) !!! 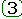 W(z) = W1(z) W2(z)  W(z, e) = Z { L-1 { Wп(s) e-ts } } = = z -1 Ze { wп[n, e ] } | 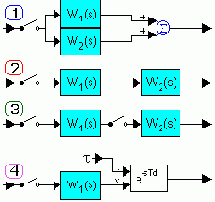 |
|
|
где: e - относительное смещение, которое отсчитывается от начала предыдущего такта (e = 1 - t/T ; 0 < t < T ). |
||
Правила преобразования структурных схем линейных систем
Декомпозиция любой линейной системы на модули (модуляризация) эквивалентна ее представлению с помощью типовых динамических звеньев. Блок-схема может содержать большое количество звеньев, и их соединение может быть произвольным. Существует лишь два основных правила преобразования структурных схем линейных систем.
Результирующая ПФ-я двух последовательно включенных блоков равна произведению их ПФ-ий.
Результирующая ПФ-я двух параллельно включенных блоков равна сумме их ПФ-ий.
Для упрощения более сложных соединений следует пользоваться принципом суперпозиции, как показано на рисунке.

Поскольку в логарифмическом домене операция умножения осуществляется сложением, результирующая ЛАЧХ последовательно включенных звеньев получается сложением исходных. Построение результирующей ЛАЧХ параллельно включенных звеньев выполняется по огибающей исходных. Здесь действует принцип – если один из параллельных каналов с изменением частоты сигнала перестает его пропускать, то сигнал проходит по второму параллельному каналу.
Предмет договора
Предметом договора являются соглашения о распространении произведения Автора: "Теория систем автоматического регулирования: Учебно-методический комплекс" (файл tau_knv.chm). Регистрационный номер в реестре Роспатента 2003612643. Далее Произведение.
Предмет, проблематика, задачи
Рабочие файлы: [САР]
Система управления
Это совокупность одного или нескольких управляемых объектов и управляющей ими системы
Принцип действия всякой системы автоматического регулирования (САР) заключается в том, чтобы обнаруживать отклонения регулируемых величин, характеризующих работу объекта или протекание процесса от требуемого режима и при этом воздействовать на объект или процесс так, чтобы устранять эти отклонения.
В теории автоматического регулирования основными являются проблемы: устойчивости, качества переходных процессов, статической и динамической точности, автоколебаний, оптимизации, синтеза и отождествления (идентификации).
Задачи общей теории автоматического регулирования заключаются в решении перечисленных проблем. При поиске решений используются:
Методы анализа устойчивости замкнутых САР
Методы оценки качественных показателей САР
Методы повышения точности САР
Методы коррекции динамических свойств САР
Методы синтеза САР
Разработка же методов решения прикладных инженерных задач стоящих при проектировании САР есть глобальная цель теории систем автоматического регулирования.
Прерыватель алгебраических петель (инициатор потока материи)
Модель прерывателя алгебраических петель – есть модель источника движущей силы нулевой величины (сравни структурные схемы). Включение идеального источника движущей силы нулевой величины в разрыв любой ветви энергетической цепи, не может изменить режим ее работы (это обусловлено нулевым внутренним сопротивлением такого источника).

Существуют модели фрагментов энергетических цепей без источников энергии, движение материи в которых вызвано ненулевыми начальными условиями на реактивных элементах. Например, модель процесса разряда конденсатора на активное сопротивление. Если проанализировать блок-схемы потребителей энергетических цепей, то становится очевидным факт возможного появления алгебраических петель, а так же простых кольцевых замыканий линий связи (смотри проводники с зелеными контактами, передающие величину потока). Как было показано ранее, включение прерывателя алгебраических петель в RC-цепь не меняет режим ее работы, но инициирует в ней поток материи и разрывает алгебраические петли, – в этом и заключено его назначение.
Таким образом, прерыватель алгебраических петель – это служебный элемент моделирующей программы, который используется последней, для показанных нужд, автоматически (по мере необходимости). Он не входит в базовые библиотеки элементов и его присутствие в ненаправленном графе (в схеме физической принципиальной) ни как не отражается.
Приглашение к членству в дискуссионной группе "Симуляция движения" (моделирование)
Уважаемые коллеги, приглашаем Вас вступить в почтовую дискуссионную группу "Симуляция движения". Будучи членом группы вы сможете обратиться с актуальными для вас вопросами к ведущим специалистам России в области моделирования. Сегодня почетными членами группы являются три коллектива разработчиков программ математического моделирования динамических систем:
Peter Darnell, президент фирмы Visual Solutions, Inc., которая разрабатывает пакет VisSim и Клиначёв Николай Васильевич, координирующий русскоязычных пользователей пакета VisSim.
Козлов Олег Степанович, представитель московского коллектива разработчиков пакета MBTY (Моделирование В Технических Устройствах).
Сениченков Юрий Борисович, представитель санкт-петербургского коллектива разработчиков программы MVS (Model Vision Studium).
Дискуссии в группе связаны с аспектами использования специализированных пакетов математического моделирования динамических систем – VisSim, Simulink (MATLAB), SystemBuild (MATRIXx), Anylogic (Model Vision Studium), MBTY, 20-sim, ITI-SIM, DyMoLa, SIMPLORER, DYNAST, hAMSter, Easy5, DASE, Electronics Workbench и т.д. Наиболее активными членами группы являются преподаватели дисциплины "Теория систем автоматического регулирования" и аспиранты соответствующих кафедр. Так же мы рады студентам.
Ключевые слова для обсуждаемых тем: симуляция движения, моделирование, управление; системы (объекты) линейные, нелинейные, непрерывные, дискретные, гибридные; инструменты частотные, корневые, вариационные, нейронные, компилирующие, оценки качества, устойчивости, быстродействия, синтеза, коррекции, оптимизации, линеаризации, программирования цифровых сигнальных процессоров - DSP, отладки в контуре модели реальных объектов.
Дискуссионные группы работают 24 часа в день, 7 дней в неделю, 365 дней в году. Их тысячи. Их работа контролируется почтовыми роботами. Робот – это специальная программа, работающая с почтой на сервере в сети. Именно она обеспечит вам общение с членами группы.
Процедура следующая. Вы пишите письмо и направляете его в группу (роботу). Робот проверяет, являетесь ли вы членом группы, и, если это так, то рассылает ваше письмо всем членам. Любой член группы может написать вам ответ. Таким образом, для участия в дискуссиях вам необходимо иметь лишь желание общаться и адрес электронной почты (e-mail).
|
АДРЕСНАЯ ИНФОРМАЦИЯ ДЛЯ УПРАВЛЕНИЯ ПОДПИСКОЙ (команды почтовому роботу) |
|
| Подписка (вступление в группу): vissim-subscribe@yahoogroups.com |
пустое письмо |
| Почтовое сообщение ко всем членам (доступно только члену группы): vissim@yahoogroups.com |
|
| Прекращение членства: vissim-unsubscribe@yahoogroups.com |
пустое письмо |
| Письмо ведущему: vissim-owner@yahoo... |
|
| Приостановка подписки (вы ушли в отпуск): vissim-nomail@yahoogroups.com |
пустое письмо |
| Переход в режим дайджеста (удобен для наблюдателей): vissim-digest@yahoogroups.com |
пустое письмо |
| Возврат в нормальный режим: vissim-normal@yahoogroups.com |
пустое письмо |
| Изменение почтовых настроек: http://groups.yahoo.com/mygroups |
|
| Адрес группы: http://groups.yahoo.com/group/vissim |
Вы посылаете пустое письмо по адресу
vissim-subscribe@yahoogroups.com. Его получает робот группы, и, минут через 15, Вы получите его ответ. Поскольку сервис Yahoo является международным, ответ робота будет на английском языке. Суть письма, сформированного для вас роботом, состоит в том, что вам предлагается два способа подтверждения подписки.
Для подтверждения вашего желания подписаться рекомендуется просто отослать письмо робота обратно, воспользовавшись кнопкой "Ответить отправителю" в инструментальной панели почтовой программы (ни каких изменений в письме делать не нужно). Получив ваш ответ, робот включит вас в список членов группы, вышлет вам приветственное сообщение и правила дискуссионной группы (уже на русском языке).
После получения правил дискуссионной группы вы можете приступать к общению с ее членами. Для этого нужно писать письма по адресу vissim@yahoogroups.com.
По адресу группы имеются дополнительные возможности:
В архив, доступный членам группы, можно положить свою интересную модель.
Вы найдете коллекцию интересных нашей группе ссылок и внесете свои.
Можете инициировать голосование и принять в нем участие.
Можете обсудить вопросы в тематическом web-форуме.
Составить краткую справку о себе для членов группы.
Настроить способ получения почты.
Если сейчас у вас нет возможности отправить письмо (т.е. вы за чужим компьютером) – воспользуйтесь желтой формой, которая приведена ниже.
| Online подписка на VisSim |
|
| Сервис groups.yahoo.com |
оценив этот сервис выше услуг серверов новостей (группа
news:fido7.ru.scada SCADA - системы автоматизации). Есть группа, обсуждающая вопросы использования в России программной и аппаратной продукции корпорации National Instruments (LabVIEW_ru-subscribe@yahoogroups.com).
19.10.2000
А. Таблица соответствия
| Энергетический домен | Координата первого рода | Координата второго рода | ||
| Электрический | электрический ток | i [А] | электрическое напряжение | u [В] |
| Магнитный | магнитный поток | Ф [Вбс-1] | магнитное напряжение | H l [А] |
| Температурный | тепловой поток | Ф [Дж К-1 с-1] | температура | q [К] |
| Гидравлический | поток объема (расход) | Q [м3 с-1] | давление | p [Н м-2] |
| Акустический | поток объема (расход) | Q [м3 с-1] | давление | p [Н м-2] |
| Механический | сила | F [Н] | скорость | v [м с-1] |
| Ротационный | момент | M [Н м] | угловая скорость | w [рад с-1] |
Б. Таблица названий законов Кирхгофа для разных энергетических доменов
| Энергетический домен |
Интерпретации законов Кирхгофа | |
| Постулат Непрерывности | Постулат Совместимости | |
| Электрический | первый закон Кирхгофа | второй закон Кирхгофа |
| Магнитный | непрерывности магнитного потока | Закон Ампера о магнитной цепи |
| Температурный | обратимого равновесия энтропии | zeroth закон термодинамики |
| Гидравлический | закон сохранения массы | принцип суперпозиции давления |
| Акустический | закон сохранения массы | принцип суперпозиции давления |
| Механический | динамического равновесия сил | принцип суперпозиции движеня |
| Ротационный | динамического равновесия моментов | принцип суперпозиции движеня |
Г. Таблица физических
| Домен | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Электрический | 1 | |||||||
| Магнитный | 2 | |||||||
| Температурный | 3 | |||||||
| Гидравлический | 4 | |||||||
| Акустический | 5 | |||||||
| Механический | 6 | |||||||
| Ротационный | 7 |
В. Таблица вариаций форм записи закона Ома в каждом энергетическом домене
| Энергетический домен |
Название технического устройства и формулировка закона Ома | ||
| активный элемент | реактивный элемент 1 | реактивный элемент 2 | |
| Электрический | |||
| Магнитный | |||
| Температурный | |||
| Гидравлический | |||
| Акустический | |||
| Механический | |||
| Ротационный |
Пример импульсной системы
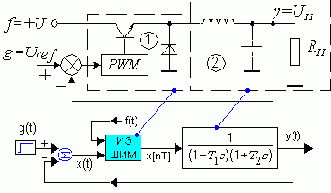
1 - импульсное звено - ключ с ШИМ; 2 - непрерывное звено - фильтр с нагрузкой; изменение +U можно рассматривать как возмущение f(t)
Система линейна, если линеен ШИ-модулятор. Если Rн
меняется, то система дополнительно будет параметрической.
