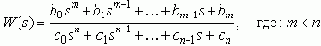Интерактивный каталог ссылок
(Каталог виден только при наличии подключения к Интернету)
Источник движущей силы (генератор энергетических потенциалов)
Иконка источника движущей силы и его внутренняя структурная схема показаны на рисунке. Логику работы модели обеспечивает неявный решатель с помощью пары блоков unknown (неизвестная) и constraint
(баланс_в_нуле) (оба блока, см. блок-схему, имеют малиновые рамки). На каждом шаге симуляции неявный решатель моделирующей программы с помощью итерационного процесса подбирает такое выходное значение блока unknown, чтобы на входе блока constraint было нулевое значение. Другими словами неявный решатель подбирает такое значение потока материи, который бы создал в подключенной к источнику цепи заданную разность потенциалов (в данной модели в качестве опорного генератора используется блок синусоидального сигнала).
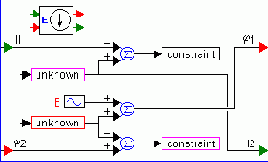
Второй блок unknown в модели (с красной рамкой) предназначен для обеспечения возможности изменения потенциалов источника в синфазном режиме. Парный этому блоку блок constraint расположен в модели физического элемента "заземлитель потенциала". Оставшийся в модели блок constraint обеспечивает нулевой баланс при возврате потока в источник (иначе, если в схеме несколько источников, то возможна ситуация, когда в данный источник вернется поток другой величины).
Источник потока (генератор потока материи)
Структурная схема источника потока материи изображена на рисунке. Величина и форма потока в данной модели задается опорным генератором – блоком синусоидального сигнала. Блок constraint заставляет неявный решатель, на каждом шаге симуляции, искать такой баланс энергетической цепи, при котором в данный источник вернется поток материи в полном объеме.
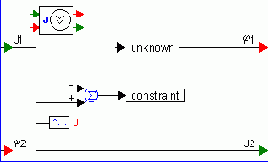
Блок unknown (в блок-схеме имеет красную рамку), так же как в модели источника движущей силы, предназначен для обеспечения возможности изменения потенциалов источника в синфазном режиме. Парный этому блоку блок constraint расположен в модели физического элемента "заземлитель потенциала".
Избранные фрагменты

Оглавление | Введение в дисциплину "Основы моделирования систем" | 1.
Введение в технологию моделирования на основе направленных графов | 2.
Введение в технологию моделирования на основе ненаправленных графов | 3. Обзор методов анализа моделей, систем и сигналов |
Литература | Архитектура моделирующих программ | Что же с ТОЭ?
Измерительные алгоритмы идентификации частотных характеристик моделей и систем
Процедуры идентификации ЧХ, основанные исключительно на спектральном или гармоническом анализе результатов измерений входного и выходного сигналов, имеют особую ценность в программах математического моделирования. Они обеспечивают наиболее эффективные и адекватные переходы от абстрактных математических моделей к проектируемым физическим прототипам и обратно, а так же являются одним из не многих инструментов оценки адекватности функционирования самих моделирующих программ в режиме симуляции.
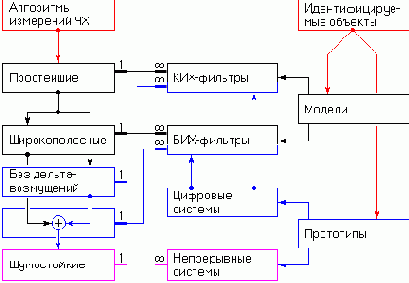
Универсальных алгоритмов измерений ЧХ нет. Существуют три вида ограничений, которые порождают семейства методов измерений ЧХ, которые в той или иной степени могут быть оптимальными для исследования трех классов идентифицируемых линейных объектов (см. рис.). К упомянутым ограничениям относятся:
Невозможность использования дельта-воздействий для объектов с эффектами насыщения.
Затруднения в расширении диапазона частот свыше "трехдекадного барьера".
Большие временные затраты на расширение динамического диапазона ниже уровня шума.
Если на вход системы подать весь спектр частот с единичными амплитудами, то определение частотной ПФ на основе измерительной информации упрощается:
W( jw) = Y( jw)/X( jw) | X( jw)=1
= Y( jw) .
Подобный единичный спектр имеет дельта-функция Дирака
d(t). Реакция же систем на дельта-функцию называется функцией веса w(t), поэтому частотную ПФ можно получить вычислением её Фурье-изображения:
W( jw) = FT { w(t) } ,
или же, для дискретных сигналов:
W [ jkw] = DFT { w[n] } = n=0N-1 еw[n] е -jkwnT .
где: w – частота первой гармоники в спектре сигнала длинной в NT выборок; k – порядковый номер гармоники (независимая переменная); N – число выборок функции веса w[n] (обычно кратно степени двойки); k Ј N/2.
Подобный подход используется в простейших алгоритмах идентификации ЧХ и достаточно легко реализуется в любых математических программах:
document.write('');
программы VisSim (в свойствах блока осциллограф активирован режим вычисления БПФ для осциллограммы)
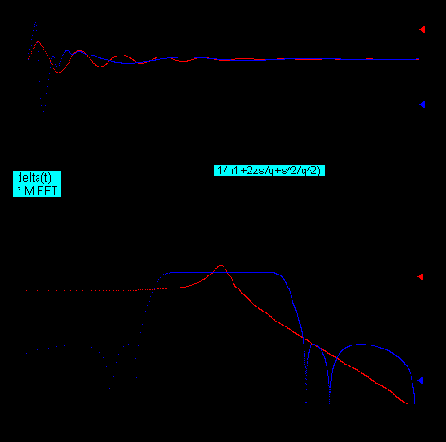
Измерения частотных характеристик выполнены для модели колебательного звена и инверсного фильтра Чебышева десятого порядка, т.е. для двух непрерывных систем с бесконечной импульсной характеристикой (IIR)
Сравнивая приведенные на рисунках ЧХ КИХ и БИХ-фильтров, легко понять суть "трехдекадного барьера" (присущего алгоритмам на базе БПФ), который проявляется при частотном анализе БИХ-фильтров, чьи ЧХ представляются в логарифмическом масштабе по оси частот. Очевидно, что, в этом случае, кратная двойке сетка анализируемых гармоник в выходном массиве процедуры БПФ ограничивает разрешение по частоте в НЧ диапазоне. Увеличение частотного диапазона на декаду требует увеличения времени симуляции в десять раз.
При измерении ЧХ реальных систем использование дельта-функции невозможно. Её замещают либо суперпозицией синусоид, либо белым шумом, либо другим сигналом конечной амплитуды. Основным методом расширения динамического диапазона ниже уровня шума является усреднение результатов повторных измерений. В случае использования алгоритмов измерения ЧХ на базе ДПФ для ослабления эффекта наложения частот используют методику взвешивания массива измерительной информации окнами Бартлета, Хэмминга, с хэннингом, Блэкмана, Хариса и т.д.
Изодромное регулирование - PI
Изодромный закон регулирования имеет вид:
u(t) = Wрег(p) x(t) = (k1 + k2/p) x(t) ,
тогда в разомкнутом состоянии система будет характеризоваться ПФ:
W(p) = Wрег(p) Wo(p) = (k1 + k2/p) Wo(p) .
В этом случае если p®0, то
W(p)®Ґ и регулирование будет астатическим. Но если p®Ґ, то W(p)®k1ko=k
и регулирование будет пропорциональным.
Резюме: PI-регулирование сочетает точность I-регулирования и быстродействие P-регулирования.
Элементы ненаправленного графа
Графические образы девяти простейших библиотечных элементов ненаправленных графов, а так же поясняющая технику подключений схема приведены на рисунке. При сборке схемы выводы разных цветов ни когда не соединяются между собой. Та же схема подключений помогает понять, почему направленные графы программ VisSim, Simulink, MVTY (при использовании описываемой методики моделирования) называют ненаправленным или бинаправленным.

Энергетические домены
Электрический
Переменные мощности: электрическое напряжение, электрический ток
Магнитный
Переменные мощности: магнитное напряжение, магнитный поток
Термальный
Переменные мощности: температура, поток энтропии
Гидравлический
Переменные мощности: давление, поток объема (расход)
Акустический
Переменные мощности: давление, поток объема (расход)
Механический
Переменные мощности: скорость, сила
Ротационный
Переменные мощности: угловая скорость, момент
| Энергетические домены | |||
| Электрический | Переменные мощности: электрическое напряжение, электрический ток | ||
| Магнитный | Переменные мощности: магнитное напряжение, магнитный поток | ||
| Термальный | Переменные мощности: температура, поток энтропии | ||
| Гидравлический | Переменные мощности: давление, поток объема (расход) | ||
| Акустический | Переменные мощности: давление, поток объема (расход) | ||
| Механический | Переменные мощности: скорость, сила | ||
| Ротационный | Переменные мощности: угловая скорость, момент | ||
| Энергия | |||
| Входы | Области на поверхности модуля, к которым подводится энергия для последующего преобразования. Энергией, которая передается модулю по оставшейся поверхности пренебрегают | ||
| Взаимодействия | Энергетический поток (потребляемая мощность) через соответствующие входы на поверхности модуля системы | ||
| Эксперимент | |||
| Натурный | Процесс наблюдения за ходом преобразования энергии динамической системой, вследствие появления некоторых вынуждающих воздействий, обычно сопровождаемый измерениями | ||
| Симуляционный | Процесс наблюдения за ходом преобразования энергии в результате симуляции движения координат модели динамической системы, вследствие появления некоторых вынуждающих воздействий, обычно сопровождаемый измерениями | ||
| Уровни моделирования | |||
| Абстракция | Выделение атрибутов модели (например: концептуальных, функциональных, физических или технологических) | ||
| Идеализация | Выбор типов взаимодействий координат модели (например: линейные или нелинейные, инвариантные или зависимые от времени, с запаздыванием, в условиях распределенных параметров, и т.д.) | ||
| Детализация | Описание модулей системы (т.е. деталей, узлов или агрегатов устройств, из которых динамическая система собрана). Здесь же описываются динамические эффекты (физические явления) возникающие в системе | ||
| mechatronics | approach to the of intelligent dynamic systems integrated across engineering disciplines | ||
| Моделирование | Переход от динамической системы к модели требуемого уровня: абстракции, идеализации или детализации | ||
| Симуляция | Процесс вынужденного движения координат модели | ||
| Интервал адекватности |
Интервалы времени, влияющих параметров и значений координат, в которых симуляция модели описывает динамическую систему с заданной погрешностью | ||
| Модель | |||
| Концептуальная | characterizes causes-and-effects in a dynamic system or system module
respecting algebraic rules |
||
| Функциональная | characterizes interrelations of variables a dynamic system or system module respecting algebraic rules | ||
| Физическая | characterizes continuous-time continuous-level energetic interactions of system modules respecting physical laws | ||
| Технологическая | model of a technological process required to produce a dynamic system | ||
| Многоуровневая | model the parts of which are considered on a different level of modeling abstraction | ||
| Мультидоменная | physical model the parts of which belong to different energy domains | ||
| Дискретная | functional model the model variables of which are approximated by discrete-time and/or discrete-level functions | ||
| Гибридная | discrete model combined with a physical model or a continuous-time continuous-level functional model | ||
| Модель | |||
| Представление | Геометрическое (отражает геометрические размеры и координаты), структурное (отражает внутреннюю топологию), поведенческое (определяет реакцию на внешние эффекты) | ||
| Описание | уравнения, структурная схема (блок-схема), графы связи (bond graph), многополюсная диаграмма (с моделями физических элементов), и т.д. + каждое описание может контролироватся графом конечного автомата, те гибридной картой состояний (гибридное моделирование) | ||
| Идентификация | Процесс определения прараметров модели базирующийся на физических гипотезах и/или эксперементах | ||
| Истиная / Ложная | |||
| Проверка адекватности | Процесс выполнения серии экспериментов с динамической системой и ее моделью (или модулем модели), цель которых - оценка величин погрешностей в движении координат и последующая проверка на удовлетворение допускам. (Сплошь и рядом результаты симуляции
движения координат абсолютно ложных по природе моделей, при каких то допусках признаются адекватными - например, для геоцентрической модели Мира). |
||
| Пременные (координаты) |
Характеризуют текущее динамическое состояние модели | ||
| Параметры | Характеризуют модель независимо от ее текущего динамического состояния (если конечно модель непараметрическая) | ||
| Модуль | |||
| Граница | geometric surface chosen in such a way that it completely encircles a system module without cutting into the boundary of any other module. The boundary itself has zero thickness, but it can be movable | ||
| Модель | Абстрактное, идеализированное представление модуля системы в той или иной форме математического описания, разработанное для ограниченного (определенного) класса симуляционных экспериментов | ||
| Многополюсник Мультиполюс |
Модель модуля взаимодействий энергии модуля системы, управляемого тремя постулатами мультиполюса module model of energy interactions of a system module governed by the three multipole postulates |
||
| Полюс | Представление скалярного взаимодействия энергии входа энергии модуля системы representation of a scalar energy interaction of an energy entry of a system module |
||
| Секция | Подмножество полюсов мультиполюса, уважая постулат мультиполюса непрерывности subset of multipole poles respecting the multipole postulate of continuity |
||
| multipole postulate of | |||
| power intake | states that the energy interactions of a multipole are fully represented by its pole-across and pole-through variables | ||
| continuity | states that the sum of all the pole-through variables of a multipole section equals to zero | ||
| compatibility | states that across variable between poles in a multipole section
equals to the difference of pole-across variables of the poles |
||
| prototype, | |||
| real | dynamic system built to verify correctness of a system design by experiments | ||
| virtual | system model set up to verify correctness of a system design by simulation experiments | ||
| reference, | |||
| across-variable | voltage of the electrical ground, temperature at the zero point on the absolute or Celsius' scale, pressure of free-space atmosphere, velocity of the absolute frame, etc. | ||
| Система | |||
| Динамическая | region in space filled with quantities of matter interrelated by energy interactions | ||
| Механическая | collection of bodies in which some or all of the bodies can move relative to one another | ||
| mechatronic | multidisciplinary system with intelligent control | ||
| Мульти- дисциплинарная |
dynamic system the investigation of which requires experts from different traditional engineering disciplines | ||
| Систем | |||
| Анализ | Подмножество задач симуляции систем связаное с использованием библиотек анализа. Различаются различные виды анализа: символьный, частотный, корневой, измерительный - операющиеся как на аналитические, так и на численные методы | ||
| Проектирование | Процесс определения структуры и параметров динамической системы, направленный на удовлетворение требований заданных критериев | ||
| Синтез | Систематизироанный и однозначный
подход к решению задачи проектирования системы |
||
| Оптимизация | Процесс подбора параметров модели системы, направленный на удовлентворение требований выбранных критериев | ||
| Отладка (Диагностика) |
Поиск причин (возможных) отказов динамической системы | ||
| Среда | Масса или область вне динамической системы | ||
| Модель | Представление динамической системы в форме абстрактного и идеализированного описания, связанного с определенным классом экспериментов | ||
| Модуль | Часть динамической системы, отделенная от системы границей модуля | ||
| Модуляризация | Процесс виртуальной декомпозиции реальной динамической системы в модули модели системы | ||
| Переменные | |||
| Мощность | Произведение парных (для каждого энергетического домена) физических величин поперечной
и продольной, которое определяет объем преобразуемой энергении в модуле системы |
||
| Поперечная (across) |
Та из парных физических величин (чье произведение есть мощность), которая фиксируется датчиком, подключеным между двумя подводами энергии к модулю динамической системы | ||
| Продольная (through) |
Та из парных физических величин (чье произведение есть мощность), которая фиксируется датчиком, установленным в разрыв любого из двух подводов энергии к модулю динамической системы | ||
| pole-across | Поперечные переменные (координаты) индивидуальных полюсов многополюсника выраженные в единицах опорной поперечной переменной | ||
| pole-through | Продольные переменные (координаты) индивидуальных полюсов многополюсника выраженные в единицах опорной продольной переменной |
Каскадные алгебраические петли
Если исходные уравнения модели системы можно представить включенными последовательно блоками, то, очевидно, что программы математического моделирования динамических систем могут однозначно выявить порядок вычислений (составить информационный поток), проверяя готовность аргументов у преобразующих данные функций. Подобный пример был рассмотрен выше.
Однако гораздо чаще в блок-схемах наблюдаются обратные связи (ОС). На рисунке приведена структурная схема апериодического звена первого порядка. Систему уравнений, соответствующую этой блок-схеме, составить легко:
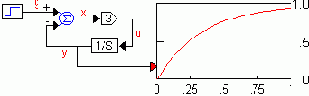
a) g = 1
b) x = g - y
c) u = 3 * x
d) y = oҐ т
u dt
e) график = y
А как составить информационный поток? Для вычисления координаты x надо знать координату y; для вычисления координаты y надо знать координату u; а для вычисления координаты u надо знать координату x. Ситуация кажется тупиковой, но это не так, и только лишь потому, что в контуре (петле) присутствует блок обладающий эффектом памяти (1/S).
Обратимся к функции, которая используется для вычисления интеграла в дискретной форме согласно методу Эйлера с запаздыванием:
y[n] = y[-1] + m=0n-1е
u[m] .
Текущее значение входного сигнала в формуле обозначено индексом n-1, выходное значение индексом n. Легко понять, что на текущем шаге выходное значение дискретного квазианалога интегратора ни как не определено текущим входным значением (связь между текущим входным значением и выходным значением на следующем шаге симуляции не отвергается). Повторим эту мысль в более общей формулировке. На текущем шаге симуляции состояние выходов всех блоков обладающих эффектом памяти не зависит от входного сигнала.
Вернемся к вопросу формирования информационного потока. В свете сказанного становится очевидно, что выходы блоков обладающих эффектом памяти порождают информационные потоки, а входы их замыкают (см. рис.).
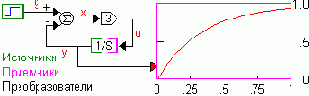
Теперь петля разомкнута, и программа может однозначно сформировать два упорядоченных, зависимых информационных потока для расчета модели:
| 1) g = 1 | 1') y = reg[n-1] + y[-1] |
| 2) x = g - y | 2') график = y |
| 3) u = 3 * x |
|
| reg[n] = reg[n-1] + u |
Если на месте интегратора будет безинерционная функция, то составить информационный поток невозможно - это и есть алгебраическая петля. Алгебраические петли появляются либо при неверном методическом подходе к решению неявных уравнений, либо при ошибочном проектировании цепей обратной связи САР (см. красную цепь на рисунке).
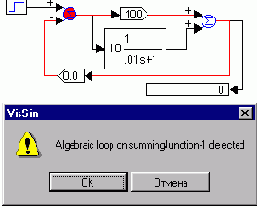
Реальные САР всегда обладают инерционными свойствами. Поэтому более точные математические модели САР обычно не содержат алгебраических петель.
Для решения неявных уравнений программы математического моделирования должны содержать неявные решатели, которые находят решение в процессе итерационного подбора. Наличие подобных решателей в программах – это следующая ступень в их развитии. Программы, преодолевшие этот барьер, как правило, позволяют описывать модели не только направленными, но и ненаправленными графами, т.е. в их библиотеках кроме математических блоков появляются физические элементы: резисторы, транзисторы, двигатели, и пр.
Каскодные алгебраические петли
В отличие от каскадных, каскодные алгебраические петли появляются в структурах функционирующих параллельно (см. рис.). В системах автоматического регулирования они встречаются редко, но любая попытка исследователя составить модель, со структурой, четко соответствующей физическим модулям реальной системы (речь о ненаправленных графах) приведет к появлению подобных структур.
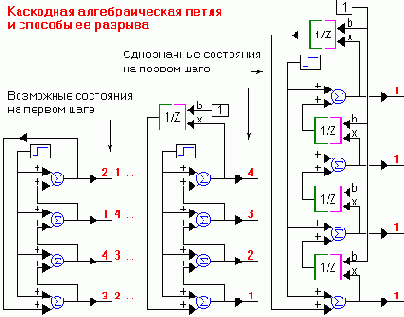
Существует несколько способов разрыва подобной петли. Разные программы математического моделирования, использующие направленные графы (VisSim, Simulink и пр.) разрывают каскодные алгебраические петли так, как показалось правильным их авторам (не предупреждая об этом пользователя). Часто точка разрыва каскодной петли, а, следовательно, и результаты симуляции меняются в зависимости от того, какие блоки подключены к выходам (происходит это по причине разной приоритетности математических операций).
Классификация систем автоматического регулирования
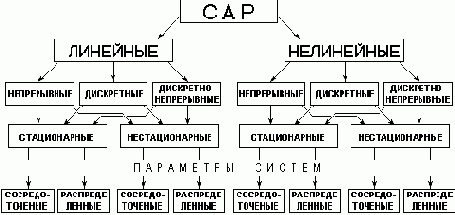
Классификация по характеру изменения величин:
Системы непрерывного действия
Системы импульсного действия (AM, ФМ, ЧМ, ШИМ, ЧИМ, ...)
Системы дискретного действия (01001011110101100010101)
Системы релейного действия
Классификация по математическим признакам:
Линейные системы
Нелинейные системы
Существенно нелинейные
Классификация по способу настройки:
Не адаптивные системы
Адаптивные системы
Системы с переменной структурой
Системы с самонастройкой программы
Системы с самонастройкой параметров
Системы с самонастройкой структуры
Классификация по типу ошибки в статике:
Статические САУ
Астатические САУ
Классификация по алгоритмам функционирования (по назначению):
Системы стабилизации
Системы слежения
Системы программного управления
Системы телеуправления
Системы самонаведения (снаряда), сопровождения (орудия), автопилотирования
Системы компенсационных измерений
...
Knv

к.т.н., доцент кафедр "Электротехника" и "Информатика" ЮУрГУ
т.р. (3512)67-90-14, т.д. (3512)34-71-62; <klinacherv_nv@mail.ru>
Основные преподаваемые дисциплины:
1) "Электротехника и электроника",
2) "Электрические и электронные аппараты",
3) "Управление техническими системами",
4) "Математические основы ТАУ",
5) "Аналоговые и аналогово-цифровые интегральные микросхемы",
6) "Информатика".
Специальность: Системы обработки информации и управления
Сфера профессиональных интересов:
Все уровни разработки любой электроники любыми методами на любой элементной базе. Программирование: C++, Pascal, Java, VB, JavaScript, HTML, ассемблеры, эмуляторы, отладчики; интегрированные среды разработки IDE; CAE/CAD системы, EDA/PCB инструменты; пакеты симулирующие движение; SCADA пакеты. Педагогическая деятельность.
Принимал участие в разработке следующих проектов:
Генератор сигналов произвольной формы.
Измерительный комплекс для снятия АФЧХ систем.
Имитатор солнечной батареи - DC/DC (для замещения последней в наземных условиях).
Прибор для измерения контактного сопротивления.
Прибор для измерения удельного сопротивления углеграфитовых изделий.
Прибор для измерения активного сопротивления обмоток электрических машин большой мощности.
Личные проекты:
Cервер "VisSim в России".
Сервер "LabVIEW в России".
Система "ИНТЕРНЕТ-КОЛЛОКВИУМ".
Библиотека измерений ЧХ систем для пакета VisSim.
Методическая работа:
Сервер кафедры "Электротехника".
Выполнение обязанностей модератора почтовых дискуссионных групп и одноименных форумов:
е-группа "Цифровая обработка сигналов в LabVIEW" (пустое письмо для подписки
е-группа "Симуляция движения и моделирование САУ в VisSim-е" (пустое письмо для подписки
Публикации (методические):
Клиначёв Н. В. Электротехника: Контрольно-тестирующая система. - Offline версия 3.0. - Челябинск, 1999. - 671 файл, ил.
Клиначёв Н.В. Моделирование обыкновенных линейных систем. ТАУ, Электроника: Руководство к лабораторным работам в пакетах VisSim и Electronics Workbench. - Челябинск, 2001. (дополнительный адрес).
Клиначёв Н. В. Теория систем автоматического регулирования и управления: Контрольно-тестирующая система. - Offline версия 3.0. - Челябинск, 2001. - 101 файл, ил.
Клиначёв Н. В. Моделирование систем в программе VisSim: Справочная система. - Online версия 1.0. - Челябинск, 2001. - 214 файлов, ил. (архив Offline версии - vsmhlpru.chm).
Литюга А. М., Клиначёв Н. В., Мазуров В. М.
Теоретические основы построения эффективных АСУ ТП: Конспект лекций. - Offline версия 1.1. - Тула, Челябинск, 2002. - 703 файла, ил.
Неизвестный автор и Клиначёв Н. В. LabVIEW в упражнениях: Учебное пособие. - Offline версия 1.0. - Челябинск, 2001. - 212 файлов, ил.
Федосов Б. Т., Клиначёв Н. В.
Теория систем автоматического регулирования: Руководство к выполнению лабораторных работ. - Offline версия 1.0 для заочного обучения. - Рудный, Челябинск, 2002. - 66 файлов, ил.
Клиначёв Н. В.
Теория систем автоматического регулирования и управления: Учебно-методический комплекс. - Offline и Online версии 1.5, 1.6, ..., 3.3. - Челябинск, 2000-2004. - 659 файлов, ил. (дополнительный
адрес).
Клиначёв Н. В.
Основы моделирования систем или 7 доменов законов Ома и Кирхгофа: Избранные фрагменты. - Offline и Online версии 1.9, 2.0, ..., 3.3. - Челябинск, 2000-2004. - 659 файлов, ил. (Распространяется в одном файле с учебно-методическим комплексом по ТАУ).
Клиначёв Н. В.
Библиотека SimLib4Visio - инструмент программирования математических ядер моделирующих программ.
- v1.2. - Челябинск, 2004. - 13 файлов.
Год начала преподавательской деятельности:1997
Рабочие языки общения: английский
Адрес: Энгельса 42-31, Челябинск, Россия, 454080
Коэффициенты ошибок
Рабочие файлы: [c1c2c3.vsm] [c1c2c3_is.vsm]
Пусть известна ПФ по ошибке Fx(s), тогда:
X(s) = Fx(s) G(s) = 1/(1+W(s)) G(s)
где: G(s) - изображение функции g(t).
Разложим Fx(s) в ряд Тейлора:
(2)
X(s) = [c0 + c1s/1! + c2s2/2! + c3s3/3! + ...] G(s) ;
перейдем к оригиналу:
x(t) = c0g(t) + c1g'(t)/1! + c2g''(t)/2! + c3g'''(t)/3! + ...
Величины c0,c1, c2, ..., cm
- называют коэффициентами ошибок. Их можно определять двумя способами:
c0 = Fx(s)|s®0, cm = [dmFx(s)/dsm]|s®0
Делением числителя Fx(s) на знаменатель и сравнением с рядом (2).
Примечания:
Коэффициенты ряда (2) непосредственно связанны с коэффициентом усиления САР, добротностями Kv, Ke, ...
| Система \ Ошибки | K & c0 | Kv & c1 | Ke & c2 |
| W(s)=1/s0 * ... | K & 1/1+K | 0 & ... | 0 & ... |
| W(s)=1/s1 * ... | Ґ & 0 | Kv & 1!/Kv | 0 & ... |
| W(s)=1/s2 * ... | Ґ & 0 | Ґ & 0 | Ke & 2!/Ke |
САР астатическая сигналу задания g(t) может быть статической для f (t), поэтому равенство нулю коэффициентов c0, c1, c2, ...
для сигнала g(t) не обязательно означает равенство нулю коэффициентов c0, c1, c2, ...
для сигнала f (t).
Ограничение количества членов ряда (2) и предположение о постоянстве коэффициентов ошибок c0, c1, c2, ...
определяет применение метода для плавно меняющихся сигналов g(t) и f (t), когда переходная составляющая в движении системы успевает затухнуть.
Комбинированное управление
Достоинства:
Наличие ООС делает систему менее чувствительной к изменению параметров регулируемого объекта.
Добавление канала(ов), чувствительного к заданию или к возмущению, не влияет на устойчивость контура ОС.
Недостатки:
Каналы, чувствительные к заданию или к возмущению, обычно содержат дифференцирующие звенья. Их практическая реализация затруднена.
Не все объекты допускают форсирование.
Корневой метод синтеза
Метод позволяет получить приемлемые динамические качества, при заданной структуре САР и заданном значении коэффициента усиления (последний член характеристического уравнения).
Пусть имеется ХУ:
(1)
sn+A1sn-1+...+An = 0.
Сумма модулей вещественных частей всех корней равна коэффициенту A1. При заданной его величине быстродействие будет максимальным, если вещественные части корней равны. Но это не достижимо - система будет не устойчивой. Например, для САР состоящей из 3-х апериодических звеньев выполнение условия эквивалентно равенству постоянных времени...
Реально всегда можно выделить 2 или 3 корня, с наименьшей по модулю вещественной частью, которые определяют вид переходного процесса. Положим их 2 и они комплексные. Перепишем ХУ:
(2)
(sn-2+C1sn-3+...+Cn-3) (s2+B1s+B2) = 0.
Достаточно рассматривать только 2-ой сомножитель, поскольку им определен вид переходного процесса:
B2 определяется значением K и должен иметь возможно большее значение.
B1 определяется суммой 2-х низкочастотных постоянных времени и связан с затуханием z, следовательно должен быть выбран исходя из 2-х противоречивых требований быстродействия и устойчивости.
Оптимальное соотношение между B1 и B2
может быть получено из условия затухания за один период z, выбор которого определяет отношение вещественной части корней к мнимой:
m = a/b = 2p / ln(1/(1-1/z)), где: a = - B1/2; b = (B2-B12/4)1/2.
Если принять, что вид переходного процесса определяют три корня, то следует воспользоваться уравнением 3-ей степени:
(3)
(...) (s3+B1s2+B2s1+B3) = 0,
которое нужно представить в виде:
(s+C11) (s2+B11s+B22) = 0.
Вещественные части корней будут равны a1 = a2,3 = - B1/3. Требования к B11 и B22 уже сформулированы, а связи с (3) определены равенствами:
B1=C11+B11, B2=B22+B11C11, B3=C11B22.
Выбор порядка уравнения для описания основной составляющей переходного процесса (2) или (3) зависит от структурной схемы САР.
Корневые методы оценки качества
Поскольку корни ПФ однозначно определяют вид переходного процесса, их можно использовать для оценки: 1)запаса устойчивости и, 2) быстродействия.
Примечание: Обычно обходятся исследованием только полюсов ПФ
F(s), т.е. корней характеристического уравнения 1+W(s)=0.

m = b/a, 0 < m < Ґ
где: a - коэффициент затухания;
b - круговая частота колебаний.
Колебательность определяет другой показатель - затухание амплитуды колебаний x(t) = Ce -a t sin(bt+j)
за период:
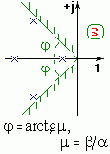
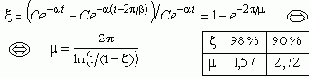
Задание определенной колебательности заставляет ограничить область расположения корней.
Колебательность системы m можно найти используя подстановку s = z e j(90-j), что соответствует повороту осей плоскости корней на угол (90-j). Далее, используя любой критей устойчивости, подбирают угол j, при котором система будет находиться на границе устойчивости. И тогда:
m = tg j = b/a.

h - это абсолютное значение вещественной части ближайшего к мнимой оси корня. Т.е. если этот корень -a±jb, то h равна коэффициенту затухания a.
И действительно, составляющая в переходном процессе xh(t) = Che -htsin(bt+j), затухает тем медленней, чем меньше h. Если в конце переходного процесса амплитуда колебаний равна DCh, то веремя переходного процесса:
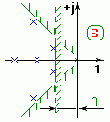
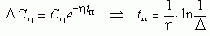
Задание определенной степени быстродействия заставляет ограничить область расположения корней.
Степень быстродействия h можно найти используя постановку s = z - hvar, что соответствует смещению корней на величину hvar. Далее, используя любой критерий устойчивости, подбирают значение
hvar, при котором система будет на границе устойчивости. И тогда: h=hvar.
Коррекция САР
Задача коррекции состоит в повышении динамической точности САР в переходных режимах. Она возникает, поскольку стремление снизить ошибки регулирования в типовых режимах, приводит к необходимости использования таких значений общего коэффициента усиления, при которых без принятия спец. мер (внедрения пассивных звеньев) система оказывается неустойчивой.
Критерий устойчивости Гурвица
Чтобы все корни ХУ:
| a1 | a3 | a5 | a7 | ... | 0 | 0 | ||
| a0 | a2 | a4 | a6 | ... | 0 | 0 | ||
| 0 | a1 | a3 | a5 | ... | 0 | 0 | ||
| 0 | a0 | a2 | a4 | ... | 0 | 0 | ||
| ... | ... | ... | ... | ... | ... | ... | ||
| 0 | 0 | 0 | 0 | an-1 | 0 | |||
| 0 | 0 | 0 | 0 | an-2 | an |
a0 s n + a1
s n-1 + ... + an-1 s + an
= 0 ,
имели отрицательные вещественные части, необходимо, при a0 > 0
выполнение условия: все n определителей Гурвица получаемые из квадратной матрицы коэффициентов должны быть положительны. Матрицы, для расчета определителей, получаются из исходной последовательным исключением последних столбца и строки.
Условие нахождения системы на границе устойчивости -
Dn = 0. Но Dn = an D(n-1) = 0, следовательно, если an = 0, то наблюдается апериодическая граница устойчивости (нулевой корень - астатическая система), а если D(n-1) = 0, то - колебательная граница устойчивости (комплексные корни).
Критерий устойчивости Михайлова
Рабочие файлы: [fr_ABCD.mcd]
Чтобы все корни ХУ:
a0 s n + a1
s n-1 + ... + an-1 s + an
= 0 ,
имели отрицательные вещественные части, необходимо чтобы после подстановки частоты в соответствующий характеристический полном D(s) полное приращение его фазы при изменении w от 0 до
Ґ составляло np/2, где: n
- степень полинома D(s). При этом характеристический полином опишет в комплексной плоскости кривую - "годограф Михайлова".
Док-во: Представим D(s) в виде разложения на линейные множители и выполним подстановку s=jw:
D(jw) = a0
(jw - s1) (jw
- s2) ... (jw - sn) ,
где: s1, s2, ..., sn
- корни ХУ. Скобки идентичны, поэтому рассмотрим одну из них. Возможны четыре основных варианта:
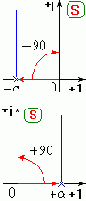

при изменении w от 0 до Ґ повернется на угол -p/2.

при изменении w от 0 до Ґ повернется на угол p/2.
при изменении w от 0 до Ґ повернутся на углы -p/2+g, и -p/2-g. Вектор, соответствующий произведению двух сомножителей, повернется на угол равный -p.

при изменении w от 0 до Ґ повернутся на углы p/2-g, и p/2+g. Вектор, соответствующий произведению двух сомножителей, повернется на угол равный p.
Резюме: Если ХУ имеет l корней с положительной вещественной частью, то угол поворота годографа D(jw) при изменении w от 0 до Ґ составит:
y = - l p/2 + (n - l) p/2 = n
p/2 - l p ,
где: n - порядок ХУ.
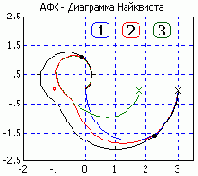
Критерий устойчивости Найквиста
Рабочие файлы: [fr_ABCD.mcd]
Чтобы система в замкнутом состоянии была устойчивой необходимо и достаточно, чтобы при изменении w от -Ґ
до +Ґ годограф разомкнутой системы W(jw)
(АФХ), поворачиваясь вокруг начала координат по часовой стрелке, охватил точку
(-1,j0) столько раз, сколько корней в правой полуплоскости содержит знаменатель W(jw).
Примечания:
Если корней в правой полуплоскости нет, то годограф W(jw) не должен охватить точку (-1, j0).
Неустойчивая система в разомкнутом состоянии может быть устойчивой в замкнутом состоянии. И наоборот.
Годограф W(jw) всегда начинается на оси "+1". Но при порядке астатизма равном r, по причине устремления W(jw) к
Ґ (при w®0), видимая часть годографа появляется только в квадранте r, отсчитанном по часовой стрелке.
Док-во:

W1(s) = 1+ W(s) = Q(s)/Q(s) + R(s)/Q(s) = D(s)/Q(s) ,
в ней D(s) - характеристический полином, Q(s) пусть не имеет корней в правой полуплоскости (пусть W(s) устойчива).
Рассмотрим угол поворота годографа W1(s). Он равен j = j1(D(jw)) - j2(Q(jw)). Поскольку степень полинома R(s) всегда меньше степени полинома Q(s), то степени полиномов числителя и знаменателя ПФ W1(s) равны. Следовательно при изменении
w от -Ґ до +Ґ:
j1(D(jw))=np
- (по критерию Михайлова), j2(Q(jw))=np
- (по предположению об отсутствии корней в правой полуплоскости у полинома Q(s)). Т.е. j=np-np=0. Другими словами для устойчивости САР в замкнутом состоянии W1(jw)
не должна охватывать начала координат, а функция W(jw) - точку (-1, j0).

j = j1(D(jw)) - j2(Q(jw)) = n p - [(n - l)
p - l p] = l 2p
,
что и требовалось доказать.
Лабораторная работа 1 ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ МОДЕЛИРУЮЩИХ ПАКЕТОВ
Рабочие файлы: [csd_new.scm] [rlc.vsm] [rlc.ca4]
Лабораторная работа 2 ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ
Рабочие файлы: [zvenya.vsm] [k((1+tp)(1+tp))^-1.ca4]
[k(1+2etp+(tp)^2)^-1.ca4] [k(p^-1).ca4]
[kp.ca4] [функц. устр. на ОУ]
Лабораторная работа 3 ПРИНЦИПЫ И ЗАКОНЫ РЕГУЛИРОВАНИЯ
Рабочие файлы: [open.vsm] [closed.vsm] [pid.ca4]
Лабораторная работа 4 АНАЛИЗ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САР
Рабочие файлы: [mihaylo4.vsm] [d_4_k&t.vsm]
[nyquist.vsm] [ou3.vsm] [ou2+1.ca4]
Лабораторная работа 6 ПОВЫШЕНИЕ ТОЧНОСТИ САР
Рабочие файлы: [1.vsm] [2.vsm] [3.vsm] [4.vsm] [5.vsm]
Лабораторная работа 7 КОРРЕКЦИЯ САР
Рабочие файлы: [k1.vsm] [k2.vsm]
[k3.vsm] [k4.vsm]
[kor_ou3.ca4] [kor_c_in.ca4]
[kor_cout.ca4] [kor_2_ou.ca4]
[kor_derv.ca4] [kor_ooc.vsm] [функц. устр. на ОУ]
Лабораторная работа 10 СИСТЕМЫ С ЗАПАЗДЫВАНИЕМ
Рабочие файлы: [e^(-st).vsm] [Вар1 e^(-st)2.vsm] [Вар2
e^(-st)2.vsm] [Вар3 e^(-st)2.vsm] [Вар4 e^(-st)2.vsm]
Лабораторная работа 12 ЦИФРОВЫЕ СИСТЕМЫ
Рабочие файлы: [Приложение1] [Приложение 2]
[Рис. 1] [Рис. 2] [err_s^-1.vsm] [k3.vsm]
Линеаризация ДУ САР
Достаточно часто встречаются звенья, имеющие нелинейную зависимость между входной и выходной координатами. Если для малых отклонений от установившегося режима нелинейность несущественна, то в этом случае до составления исходных ДУ САР (1), ..., (5). Выполняют процедуру линеаризации.
Линейные непрерывные законы регулирования
Под законом регулирования (управления) понимается алгоритм или функциональная зависимость, определяющая управляющее воздействие u(t)
на объект:
u(t) = F(x, g, f) .
Линейные законы описываются линейной формой:
u(t) = k1x(t) + k2тx(t)dt
+ k3ттx(t)dt2
+ ... + k4x'(t) + k5x''(t) + ...
она же в операторной форме записи:
(1*)
u(t) = x(t) [k1
+ k2/p + k3/p2
+ ... + k4 p + k5 p2
+ ...] .
Наличие в (1*) чувствительности регулятора к пропорциональной, к интегральным или к дифференциальным составляющим в первичной информации x(t), определяет тип регулятора:
P - пропорциональный.
I - интегральный.
PI - пропорционально интегральный (изодромный).
PD - пропорционально дифференциальный.
и более сложные варианты - PID, PIID, PIDD, ...
ЛИТЕРАТУРА
Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - М.: Наука, 1975.
Лукас В. А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.
Брюханов В. Н. и др. Теория автоматического управления. –М: Высшая школа, 2000 г.
Острём К., Виттенмарк Б. Системы управления с ЭВМ: Пер. с англ. - М.: Мир, 1987. - 480 с., ил.
Оппенгейм Э., Шафер Р. Цифровая обработка сигналов/ Пер. с англ./ Под ред. С. Я. Шаца. - М.: Связь, 1979. - 416 с.
Антонью А. Цифровые фильтры: анализ и проектирование/ Пер. с англ. - М.: Радио и связь, 1983. - 320 с.
Гольденберг Л. М., Матюшкин Б. Д., Поляк М. Н. Цифровая обработка сигналов: Справочник. - М.: Радио и связь, 1985. -312 с., ил.
Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения: В 2 т./ Пер. с англ. Ф. М. Писаренко с предисловием А. М. Яглома - М.: Мир, 1971.
Сборник задач по теории автоматического регулирования и управления/ Под редакцией В. А. Бесекерского. - M.: Наука, 1978.
Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. - М.: Наука,1986.
Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство/ Пер. с нем. - М.: Мир, 1982.
Хоровиц П., Хилл У. Искусство схемотехники: В 3 т./ Пер. с англ. - М.: Мир, 1993
Остапенко А. Г. Анализ и синтез линейных радиоэлектронных цепей с помощью графов: Аналоговые и цифровые фильтры. - М.: Радио и связь, 1985. - 280 с., ил.
Кадыров А. А. Динамические графовые модели в системах автоматического и автоматизированного управления. -Ташкент: Фан, 1984. - 239 с. :ил.
Зыков А. А. Теория конечных графов. - Новосибирск: 1969.
Узловая Продольная Вынуждающая Потенциальная Пересекающая Силова, сквозная поточная
1) Для каждого энергетического домена разработаны альтернативные, матричные методы расчета соответствующих систем. Например, в электрическом домене к ним относятся: "Метод контурных токов", "Метод узловых потенциалов" - они тоже могут использоваться для составленя графов. Вспомним цель разработки этих методов. Она состояла только в одном - в сокращении размерности системы уравнений, причем за счет отдаления описания от физического смысла. Компьютерное моделирование понижает ценность этих методов, поэтому для унификации подхода рекомендуется составлять графы согласно методу расчета, использующему первый и второй законы Кирхгофа.
2) И для одного энергетического домена закон Ома может иметь несколько форм записи. Например, для электрического домена формула закона Ома отлична для активного сопротивленя, индуктивного и емкостного.
3) Здесь не рекомендуется использовать дословный перевод терминов across and through variables, как поперечная и продольная переменные
(координаты или физические величины). В русском языке, для данной тематики, такой перевод вносит путаницу на уровне интуитивно воспринимаемых оттенков.
3.04.2002
Клиначёв Н. В. Основы моделирования систем или 7 доменов законов Ома и Кирхгофа: Избранные фрагменты. - Offline версия 3.1. - Челябинск, 2000-2004. - 68 файлов, ил.
– Website: http://www.vissim.nm.ru/oms_lec.html.
Клиначёв Н. В. О структурном кризисе в методике преподавания блока дисциплин связанных с расчетом цепей преобразования энергий. - Челябинск, 2003.
- Website: http://www.vissim.nm.ru/lectures/sml_06.htm.
Клиначёв Н. В. Введение в технологию моделирования на основе направленных графов. - Челябинск, 2003.
– Website: http://www.vissim.nm.ru/lectures/sml_02.htm.
Клиначёв Н. В. Введение в технологию мультидоменного физического моделирования с применением ненаправленных графов. - Челябинск, 2003.
– Website: http://www.vissim.nm.ru/lectures/sml_03.htm.
Герберт Шилдт. Самоучитель C/C++: пер. с англ. - 3-е издание. - СПб.: БХВ Петербург, 2001. - 688 с.
Microsoft Corporation. Microsoft® Windows Script Technologies Development Center. – Website: http://msdn.microsoft.com/scripting.
Microsoft Corporation. Microsoft® XML Development Center. – Website: http://msdn.microsoft.com/xml.
Microsoft Corporation. Microsoft® Visio Development Center. – Website: http://msdn.microsoft.com/visio.
National Instruments Corporation. NI® Measurement Studio Development Center. - Website: http://www.ni.com/mstudio.
Multipole modeling of multidisciplinary systems. — Website: http://virtual.cvut.cz/course, Czech Technical University in Prague, 2001.
Controllab Products B. V. Справочная система программы 20-Sim. — Website: http://www.20sim.com, Netherlands, 2001.
Бессонов Л. А. Теоретические основы электротехники: Электрические цепи. — М: Высш. школа, 1978. — 528 с., ил.
Клиначёв Н. В. Моделирование систем в программе VisSim: Справочная система. — Offline версия [vsmhlpru.zip]. — Website: http://vissim.nm.ru/vsmhlpru.zip, http://vissim.nm.ru/help/vissim.htm, Челябинск, 2002.
либо в виде отношения их разложений на элементарные множители:
(1)

Постановка s¬jw
позволяет перейти в частотный домен. При наличии ЭВМ построение ЛАЧХ & ЛФЧХ не составит труда в любом случае. Однако разложенная на множители ПФ (1) позволяет построить асимптотические ЛАЧХ & ЛФЧХ практически без вычислительной работы. Каждый линейный множитель ее числителя и знаменателя есть комплексное число. Найдем модуль каждого (как гипотенузу прямоугольного треугольника), и перейдем к логарифмическому масштабу:
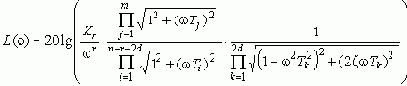
Для упрощения дальнейших построений избавимся от операции умножения, заменив ее операцией сложения в логарифмическом домене:
(2)
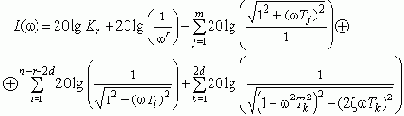
Легко понять, что каждое слагаемое выражения (2) есть либо прямая линия, либо асимптотически приближается к прямым линиям при устремлении частоты к нулю и к бесконечности. Наклон аппроксимирующих прямых всегда кратен 20 дБ за декаду.
Для построения ЛФЧХ необходимо найти фазу каждого множителя числителя и знаменателя частотной ПФ, как арктангенс отношения его противолежащего катета к прилежащему (напомним, что при произведении комплексных чисел (в экспоненциальной форме) фазы (показатели степени) складываются, а при делении - вычитаются). Таким образом, построение ЛФЧХ производится по выражению:
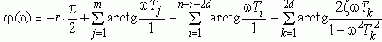
Отметим так же, что одному Белу соответствует увеличение мощности в 10 раз. Поскольку A - это физическая величина либо первого, либо второго рода, а не их произведение (т.е. не мощность); увеличение ее в 10 раз соответствует увеличению мощности в 100 раз, что соответствует двум Белам или 20 дБ.
Мастер для генерации коэффициентов дискретного фильтра
Встроенный ниже в html-страницу мастер корректно визуализируется и функционирует в браузере MSIE 5.0. Отображение мастера меняется не существенно в браузере Opera 6.04, и логика работы с мастером не нарушается. В браузере Netscape 7.0 мастер не работает.
Три коэффициента числителя (b0, b1, b2) и три коэффициента знаменателя (a0, a1, a2) z-ПФ в соответствующем порядке выводятся мастером в двух нижних строках. В качестве разделителя используется пробел. Рекомендуется пользоваться клавиатурным копированием (Ctrl+c и Ctrl+v) для переноса коэффициентов в блок "Передаточная функция" моделирующей программы. Для перехода между полями формы используйте клавиши Tab и Shift+Tab.
| БИХ-фильтр второго порядка | ||
| Тип: | ФНЧ
ФВЧ ПФ РФ ФВФ ПФФ Ф-НЧС Ф-ВЧС | |
| Добротность
Полоса (тех) Полоса (муз) : |
= f/Df | |
| Добротность
Наклон (тех) Наклон (муз) : |
= f/Df | |
| К в полосе: | [дБ] | |
| Аналоговый прототип (w=1): | ||
| k: Числ: Знам:
|
||
| Дискретный фильтр: | ||
| 1/dT: | [Гц] | |
| Частота: | [Гц] | |
| Числ: Знам: |
||
init_form();
Приведенная ниже форма позволяет на основе коэффициентов рассчитанных мастером построить частотные характеристики соответствующего дискретного фильтра. Скрипт считает ЧХ именно дискретной системы, а не ее линеаризованного аппроксиматора (в большинстве моделирующих программ для построения ЧХ дискретной системы выполняется обратное БЛП и строятся ЧХ линеаризованного аппроксиматора). С ознакомительными целями Вы можете выполнить расчеты для выбранных по умолчанию установок. Поскольку графики строятся в Excel'е, Вы должны ответить положительно на вопрос системы безопасности программы MSIE о том запускать ActiveX компонент (Excel) или нет.
| Построение ЛАЧХ & ЛФЧХ (в Excel'e) | |
| Начальная частота: | [рад/с] |
| Считать для декад: | 2
3 4 5 (100 точек / дек) |
| + АЧХ & ФЧХ: | ( + 30 сек ) |
Математическое моделирование на
Мир технических систем в 7 раз проще,
чем мы о нем думаем сейчас
Графов теория
Учение об общих топологических свойствах графов и о вытекающих из них расчетных методах. Две ветви теории: теория направленных графов
и тероия ненаправленных графов четко делят между собой программы визуального математического моделирования.
Граф направленный (сигнальный)
Диаграмма прохождения сигнала, состоящая из совокупности узлов (сумматоров) и соединяющих их ветвей. Стрелки на ветвях указывают направление передачи сигнала или воздействия от одгого узла к другому. Ветви в направленном графе характеризуются передаточными функциями. Направленный граф является графической формой записи системы уравнений описывающих динамическую систему, и не может отражать ее топологию (модульную структуру).
Узел направленного графа
Сумматор координат модели динамической системы с одним выходом (поэтому узел направленного графа называют координатой). Обычно в каждом энергетическом домене в качестве координат выступают парные физические величины, чье произведение есть мощьность. В пакетах математического моделирования эти парные физические величины называются координатами первого и второго рода. Выходные координаты ветвей собираются в узлы направленного графа согласно первому и второму законам Кирхгофа1. Узлы направленного графа, ровно как и сам граф, не отражают различий в физической природе координат первого и второго рода (это непреодолимый недостаток направленных графов).
Ветвь направленного графа
Графический образ закона преобразования сигнала, который называется передаточной функцией. Если направленный граф есть истинная модель динамической системы и узлы графа отражают все ее координаты (граф не приведен), то передаточные функции ветвей есть либо закон Ома2, сформулированный для соответствующего энергетического домена и связывающий его физические величины первого и второго рода, либо другие физические законы, связывающие физические величины первого и второго рода разных энергетических доменов.
Граф ненаправленный (топологический)
Схема, состоящая из совокупности соединенных в узловых точках двух- или ?многополюсных модулей? преобразующих энергию. Полюсы многополюсников являются подводами энергии. Для ветвей ненаправленного графа нельзя однозначно указать направление распространения коордитаты первого рода. Ненаправленный граф зеракльно (без искажений) отражает топологию (модульную структуру) динамической системы, и в том же графическом образе, но как в нелинейном зеркале, отражается ее система уравнений. Для узлов ненаправленного графа можно записать первый закон Кирхгофа, а для контуров - второй закон Кирхофа.
Узел ненаправленного графа
Условное графическое обозначение технического устройства - узлового распределителя физической величины первого рода. В динамике, поток (физическая величина первого рода) любой ветви входящей в узел может менять свое направление.
Ветвь ненаправленного графа
Участок цепи ненаправленного графа, для которого координата первого рода имеет неизменное значение. Ветвь ненаправленного графа содержит условное графическое обозначение одного технического устройства или нескольких, но инкапсулированных в один модуль.
Контур
Для направленных и ненаправленных графов, это замкнутый путь проходящий через несколько узлов и ветвей.
Координата первого рода (through variable3)
Отражение в модели той из парных физических величин (чье произведение есть мощность), которая фиксируется датчиком, установленным в разрыв любого подвода энергии к модулю динамической системы. Во всех энергетических доменах физические величины первого рода подчиняются первому закону Кирхгофа.
Координата второго рода (across variable3)
Отражение в модели той из парных физических величин (чье произведение есть мощность), которая фиксируется датчиком, подключеным между любыми двумя подводами энергии к модулю динамической системы. Во всех энергетических доменах физические величины второго рода подчиняются второму закону Кирхгофа.
Метод корневых годографов
Рабочие файлы: [root_locus.vsm]
Метод позволяет подобрать параметры системы по оценке их влияния на общую картину расположения корней замкнутой САР.
Если ПФ замкнутой САР:
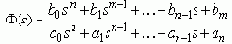
то полюсы и нули (корни) всегда можно вычислить и нанести на комплексную плоскость. Если менять один из параметров системы, (K, ..., Ti, ..., z), то изменения в ПФ F(s) приведут к смещению корней - движению по траекториям, совокупность которых называется корневым годографом. Если менять один параметр, при дискретных значениях другого, то можно оптимально выбрать значения уже 2-х параметров, оценивая семейство корневых годографов. При выборе допустимо пользоваться любой из корневых оценок качества: m, h,
W0.
Наиболее эффективен метод при выборе K. ПФ разомкнутой системы и ХУ запишем в виде:
(*)
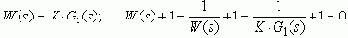
здесь s - не оператор Лапласа или дифференцирования, а любой из корней!!!
Если корни - полюсы и нули известны (q1o, q2o, ..., qmo; q1x, q2x, ..., qnx), то операторную часть ПФ - G1(s) можно представить в виде:
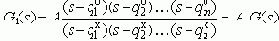
где:
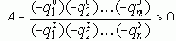
Представим сомножители (s - qi) векторами:
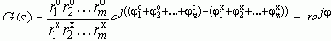
Теперь вновь запишем ХУ:
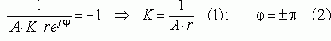
При изменении K от 0 до бесконечности уравнения (1) и (2) определяют правила движения корней:
Если K=0, то корни ХУ (*) совпадают с полюсами W(s), т.к. G(s) должна стремится к бесконечности.
Если K®Ґ, то часть корней ХУ (*) совпадают с нулями W(s), а часть уходит в бесконечность, т.к. G(s)®0 как при совпадении s с нулями, так и при s®Ґ. Наклон асимптот для уходящих в бесконечность корней можно рассчитать по формуле:
(p+2ip) / (n-m), где: i=1,2, ..., n-m.
Метод логарифмических амплитудных характеристик
Процесс синтеза включает в себя следующие операции:
Построение располагаемой ЛАЧХ исходной системы Wo, состоящей из регулируемого объекта без регулятора и без корректирующего устройства.
Построение НЧ части желаемой ЛАЧХ на основе предъявленных требований точности.
Определение вида и параметров регулятора K, Ki, ...:
| Wрег(s) = WНЧ.ж.(s) / Wo(s); | Lрег(w) = LНЧ.ж.(w) - Lo(w
) . |
Уточнение ВЧ части желаемой ЛАЧХ на основе требований к запасу устойчивости - LНЧ&ВЧ.ж.(w).
Определение вида и параметров последовательного корректирующего устройства:
| WПЗ кор = WНЧ&ВЧ.ж.
/ [Wрег Wo]; |
LПЗ кор = LНЧ&ВЧ.ж. - Lрег
- Lo . |
Техническая реализация корректирующих устройств. В случае необходимости - перерасчет на эквивалентные параллельное звено или ОС.
Поверочный расчет и построение переходного процесса.
Методика вывода дискретных ПФ
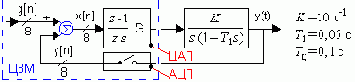
Работу ЦВМ обеспечивают АЦП (квантователь) и ЦАП (экстраполятор нулевого порядка), следовательно:
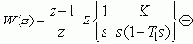
Для нахождения z-изображения непрерывной ПФ W(s) по таблицам, последнюю надо разложить на элементарные дроби, т.е. преобразовать к параллельной структуре. Тогда на каждое простейшее звено сигнал будет поступать с квантователя (что и требуется при использовании таблиц):

где:
A (1+T1s) + Bs (1+T1s) + Cs2 = 1 ;
(BT1+C) s2 + (AT1+B)
s + A = 0s2 + 0s + 1 ; =>
=> A = 1, B = -T1, C = T12 .
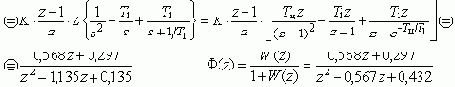
Методы повышения запаса устойчивости
Демпфирование с подавлением высоких частот
Демпфирование с подавлением средних частот
Демпфирование с подавлением низких частот или эквивалентным поднятием высоких
Демпфирование с введением дополнительных фазовых сдвигов
Моделирование в программе Electronics Workbench
| Модели устройств выборки хранения (УВХ): | [yvx1.ca4] [yvx2.ca4] [yvx3.ca4] [yvx4.ca4] |
| ЦАП на ШИ-модуляторе: | [dac_pwm.ca4] |
| Последовательный ЦАП на переключаемых конденсаторах: | [dac_2c.ca4] |
| Параллельный ЦАП на R-2R матрице постоянного импеданса: | [dac_r2r.ca4] |
| Параллельный ЦАП на коммутируемых конденсаторах: | [dac_nc.ca4] |
| ZCS-1/2 FMИИВЭП | [zcs_01.ca4] |
Моделирование в программе VisSim
| К пояснению взаимосвязей между шагом симуляции, методами интегрирования и частотным анализом: | [1_s_x_2.vsm] |
| Переходный процесс в "RLC" схеме: | [rlc.vsm] |
| Модели измерителей электрических величин: | [rms_ex.vsm] [meter.vsm] |
| Поиск корней уравнения: | [roots.vsm] |
| Звенья с модулированным сигналом: | [fil_resp.vsm] [pwm_ex.vsm] |
| Звено чистого запаздывания: | [vtcdelay.vsm] |
| Релейные САР: | [roomctrl.vsm] |
| Импульсные САР: | [bworth.vsm] |
| Диаграмма Вышнеградского: | [vishngrd.vsm] |
| Линии уровня показателя колебательности М: | [m.vsm] |
| W(s) на основе характеристического полинома D(s): | [order3.vsm] |
| Коррекция САР, коррекция жесткой ОС & изодромный блок на апериодическом звене: |
[2ou+kor.ca4] [ouhik&f1.vsm] [kor_ooc1.vsm & kor_ooc2.vsm] |
| Дельта-сигма АЦП: | [adc_dsigm.vsm] |
| Импульсная характеристика КИХ-фильтра: | [fir.vsm] |
| Универсальные блок-схемы для составления моделей: | [tf_univr.vsm] |
| Прямое и обратное быстрые преобразования Фурье (БПФ): | [fft.vsm] |
| Ряды Фурье: | [furye1.vsm] |
| Измерение ЧХ КИХ и БИХ систем по их импульсной характеристике: | [fr_FIR_fft50.vsm] [fr_IIR_fft50.vsm] |
| Оценка мощности спектра сигнала: | [psd.vsm] |
| Генераторы на z-ПФ с начальными условиями: | [gen_z.vsm] |
| Прототип электронного аналогового синусоидального преобразователя: | [sin.vsm] |
Модульная структура программ математического моделирования динамических систем
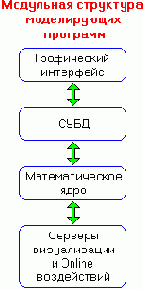
Рис. 1
Сколь разными бы ни казались моделирующие программы, их модульная структура практически неизменна (см. рис.1):
Графический интерфейс ориентирован на человека и отвечает за представление математической модели в виде, понятном широкому кругу специалистов. Это могут быть блок-схемы, схемы физические принципиальные, гибридные карты состояний и пр.
Система управления базой данных отвечает за хранение объектов составленной пользователем модели и требуемые трансформации структуры ее хранилища.
Математическое ядро берет на себя основную вычислительную нагрузку, и, в цикле, согласно заданной программе, руководствуясь готовностью аргументов, а в редких спорных случаях (появление которых всегда можно избежать) приоритетностью математических операций, обеспечивает исполнение потоков математических функций.
Серверы визуализации и Online воздействий обеспечивают интерфейс между функционирующим математическим ядром и пользователем. Серверы визуализации результатов — осциллографирующие, показывающие, и индицирующие приборы — в зависимости от ситуационных требований, могут работать либо в синхронном, либо в асинхронном режиме. Серверы же Online воздействий на модель жестко синхронизированы с математическим ядром.
К большому сожалению разработчики моделирующих программ при создании своих продуктов не придерживаются современных технологий модуляризации (COM, CORBA) и предпочитают все делать самостоятельно. Их консерватизм в этом отношении создает потенциально неустойчивую ситуацию на рынке. Все представленные на рис. 1 модули могут быть не просто автономными, а уже традиционно считаются независимыми программными продуктами. Ирония в том, что математическое ядро — это наиболее простой и легкий в создании модуль. Совершенно очевидно, что создание полноценного редактора векторной графики подобного Visio или CorelDraw или же движка реляционной базы данных — это задача не для фирмы со штатом из 3..10 человек. Именно усилия, потраченные на решение этих второстепенных задач, разорили далеко не одну компанию, а проигрывают от этого пользователи.
За последние десять лет ситуация изменилась не в пользу описанной позиции разработчиков моделирующих программ. Вспомогательные модули созданы конкурирующими между собой сторонними производителями, широко доступны, обеспечивают требуемые механизмы интеграции с другими программными комплексами и непрерывно совершенствуются профессионалами в своей области.
Рассмотрим вариант перспективного модульного состава моделирующей программы (см. рис. 2). Даже беглая оценка списочного состава модулей выдает владельца используемых программных технологий — корпорацию Microsoft. Далее мы лишь добавим парочку скриптов и COM-серверов, наиболее важным из которых является математическое ядро.
Итак, в качестве графического интерфейса из двух кандидатов был выбран пакет векторной графики Visio, который чуть более популярен у инженеров, чем у художников. Для управления текстовым хранилищем модели с XML-разметкой был выбран не большой, бесплатно распространяемый, имеющий качественную документацию, и присутствующий на каждой машине с ОС Windows движок реляционной базы данных — COM-сервер (файл msxml*.dll). Выбор последнего вспомогательного компонента — сервера визуализации (объекта MSGraph.Chart программы Excel) не оптимален, не перспективен и определен лишь фактом его широкого распространения на машинах читателей этой статьи. Безусловно, здесь более подойдет инструментарий визуализации практически любой SCADA-системы, а лучше — библиотеки "Mearsurement Studio" for Visual Basic and Visual C++ фирмы National Instruments [9].

Рис. 2
Необходимое условие устойчивости САР, достаточное только для систем 1-ого и 2-ого порядков
Чтобы корни ХУ имели отрицательные вещественные части, необходимо чтобы все его коэффициенты были положительны. Однако это условие является достаточным только для систем 1-ого и 2-ого порядков. Док-во:
ХУ
a0 s n + a1
s n-1 + ... + an-1 s + an
= 0 ,
представим в виде:
a0 (s - s1) (s
- s2) ... (s - sn-1) (s
- sn) = 0 ,
где: s1, s2, ... sn-1, sn - корни.
В устойчивой системе вещественные части корней отрицательны. Подставим такие корни: s1= -a1; s2 = -a2; s34 = -a3±jb ... :
a0(s+a1)(s+a2)(s+a3-jb)(s+a3+jb) ... = a0(s+a1)(s+a2)((s+a3)2+b2) ... = 0
Если раскрыть скобки и вернутся к стандартному виду ХУ, то все коэффициенты уравнения получатся положительными.
О демонстрационных версиях программы VisSim
Студенческая версия программы VisSim не имеет достаточного количества примеров, для раскрытия всех ее возможностей. Преподавателю рекомендуется ознакомиться с демонстрационными версиями, которые можно найти на сайте фирмы Visual Solutions Inc.:
VisSim\Analyze - базовая версия, включающая библиотеку частотного анализа.
VisSim\TI-C2000 Rapid Prototyper - версия для специалистов в области электропривода (включает моторы, регуляторы на ЦСП (DSP) и т.д.).
VisSim\Comm - версия для связистов (включает источники, шифраторы, модуляторы, каналы связи, демодуляторы, дешифраторы, фильтры и т.д.).
VisSim\SigPro - версия для специалистов работающих с сигналами аудио диапазона.
VisSim\ModelWizard - дополнительный инструментарий, не включающий VisSim, нужный специалистам по идентификации объектов по историческим данным (по переходным процессам).
Только одна демо-версия VisSim\Analyze позволяет полностью изучить модели входящие в учебно-методический комплекс, поскольку остальные не имеют требуемой библиотеки частотного анализа. Все демо-версии полнофункционально работают 60 дней. После 60 дней демо-версии перестают сохранять рабочие файлы, а библиотека частотного анализа отключается (сохранение учебных моделей не предполагается).
О компенсации помех в астатических системах
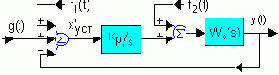
Рассмотрим вторую составляющую ошибки x''уст от возмущающих воздействий fko. Если САР астатическая, то W(s)|s®0®Ґ, но возможен случай, когда Wfk(s)|s®0®Ґ. Т.е. при любой степени астатизма САР x''уст может быть отличной от нуля.

Резюме:
Для подавления ошибки от возмущения необходимо, чтобы интегрирующий элемент был включен в контур до места приложения возмущения.
Если рассматривать ошибку чувствительного элемента (сумматора) как возмущение, то, очевидно, что повышение степени астатизма не позволяет устранить ее.
О синтезе систем с ЦВМ методом логарифмических амплитудных характеристик

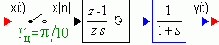
Изображенный дискретный фильтр имеет в области частот
w ЛАЧХ & ЛФЧХ, использовать которые при синтезе неудобно.
Перевод с помощью v-преобразования ЧХ в область псевдочастот l, позволяет получить ЛАЧХ, которые по виду подобны ЛАЧХ непрерывных систем.
Последовательность преобразований следующая:
Wэ(s)ЧW(s) ® W(z) ®
W(v) ® W(jlTц/2).
Эти преобразования при использовании экстраполятора нулевого порядка могут быть формализованы. Пусть ПФ непрерывной части имеет вид:
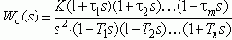
Техническая реализуемость систем с ЦВМ позволяет ввести положения:
Пусть для частоты среза непрерывной части выполняется условие
wср < 2/Tц.
Все постоянные времени знаменателя разделим на две группы - до и после диапазона от частоты среза до частоты дискретизации:
T1, ..., Tq > (1/wср
... 1/wц) > Tq+1, ..., Tn.
Постоянные времени в числителе t1, ...,
tm пусть больше чем 1/wср.
Поскольку система должна быть устойчива, пусть наклон ЛАЧХ на wср
будет -20 дБ/дек.
Принятые положения, позволяют описать свойства систем в области низких и высоких частот двумя ПФ:
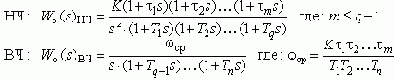
Теперь для формального перехода в область псевдочастот
l (минуя промежуточные z и v-преобразования) достаточно подставить в ПФ Wo(s)НЧ
вместо s jl и умножить ее на множитель (1-jlTц/2), для низких частот приближенно равный 1.
А ПФ Wo(s)ВЧ будет соответствовать выражение:
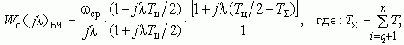
Модуль которого:
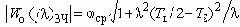
Результирующий фазовый сдвиг обеих областей:

Резюме:
В области НЧ (w < 2/Tц) асимптотическая ЛАЧХ системы с ЦВМ практически сливается с ЛАЧХ непрерывной части (множитель (1-jlTц/2) » 1)
и можно положить l » w. Это позволяет один к одному использовать разработанную для непрерывных систем методику формирования НЧ части желаемой ЛАЧХ.
В области ВЧ отличия вносит множитель (1-jlTц/2), ухудшающий условия устойчивости. Поэтому при формировании запретной ВЧ области в расчетных формулах величина Tц/2 должна быть просуммирована с малыми постоянными времени:
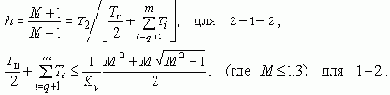
О студенческой версии программы VisSim
Для изучения моделей, входящих в учебно-методический комплекс и организации учебного процесса требуется загрузить студенческую версию программы VisSim, см. раздел "Download" сайта "VisSim в России". Данная версия программы специально предоставлена пользователям этого учебно-методического комплекса фирмой Visual Solutions Inc. Условием правомочного использования бесплатной студенческой версии является регистрация пользователя.
Пройти процедуру регистрации можно на сайте фирмы путем заполнения
формы-требования демонстрационных версий программы VisSim. На вопрос о том, как вы узнали о программе (How did you hear about VSI / VisSim?) вам рекомендуется указать адрес, с которого вы загрузили студенческую версию (например, http://vissim.nm.ru/setupVisSimFAC.zip). Большая просьба: заполняйте форму английскими буквами.
Студенческая версия является эквивалентом действовавшей ранее "Бесплатной Академической Программы распространения VisSim'а", которой мог воспользоваться лишь преподаватель вуза.
Фирма Visual Solutions Inc. готова поставить русскоязычным вузам платную, полную, русифицированную версию программы.
О том, как программы мультидоменного
Известно много хороших математических программ. В наших целях каждую программу можно отнести к одной из двух групп:
Мощные калькуляторы для статических вычислений (Matcad, Mathematica, Maple).
Специализированные решатели для моделирования динамических процессов (DyMoLa, Dynast, Multisim, VisSim, MBTY, MVS, Simulink).
Применение в обучении первой группы программ для расчета цепей преобразования энергий возможно, не вызывает ни каких затруднений, гладко согласуется со всеми методиками изложенными в учебниках по "теоретическим основам", отвечает требованиям Министерства образования, но не имеет ни какого смысла. Вспомним о том, что лишь 20 страниц из учебников по "теоретическим основам цепей" дают студенту фундаментальные знания (о законах Ома и Кирхгофа). Остальная информация – это изложение жестко формализованных методов, не дающих студенту новых знаний (выберите направление токов, посчитайте количество узлов, и пр.). Сейчас уже мало кто помнит, но главной целью разработки всех альтернативных методов расчета цепей было сокращение объема вычислений. Сегодня любой "универсальный калькулятор" (Matcad, Mathematica, Maple) рассчитает любую цепь, любым методом за десятые доли секунды. Это прогресс, это замечательно, но надо сказать, что мгновенные вычисления на "калькуляторах" не добавляют знаний студентам. Возникает так же более серьезный вопрос. Как объяснить студенту, зачем ему требуется зубрить альтернативные методы, когда он может выполнить проектирование любой цепи, преобразующей энергию, разобравшись лишь с законом Ома и законами Кирхгофа? Уже сегодня вразумительного ответа на поставленный вопрос нет.
Однако кроме методов расчета цепей, учебники по "теоретическим основам" содержат описания подходов к решению задач, которые были упомянуты выше. Ценность этой информации низвели до нулевого уровня программы второй группы. Их разработчики справедливо предположили, что задачи первых трех уровней сложности (см. список выше), можно решать с помощью математического аппарата, применяемого для решения задач четвертого уровня. Таким образом из учебника по "теоретическим основам" упомянутые программы взяли на вооружение лишь законы Ома и Кирхгофа, используя их в дифференциальной форме.
Об альтернативном построении графа схемы физической принципиальной
Рабочие файлы: [Альтернативные элементы] [codirected_bond_graphs.vsm]
Большинство программ для математического моделирования динамических систем (VisSim, Simulink, MBTY) в своем графическом интерфейсе предоставляют возможность собрать проводники в шину. Но направления проводников в шинах должны совпадать. Это вызывает затруднения при использовании предложенной библиотеки элементов. Однако, следуя этому ограничению, можно составить альтернативную библиотеку, элементы которой можно будет соединять подобными шинами. Принципиальных отличий в построении альтернативной библиотеки нет, и требуемые модификации не существенны. В моделях пассивных элементов ненаправленного графа меняется знак на сумматоре при вычислении приращения потенциала, а та часть блок-схемы распределяющего узла, которая отвечает за баланс потенциалов, перемещается в аккумулирующий узел.
Об авторстве
В любой момент авторство КлиначёваН. В. на данный учебно-методический комплекс (далее цифровой документ) может быть подтверждено. Дайджест данного файла (для цифрового документа это эквивалент отпечатка пальца) зашифрован закрытым ключом Клиначёва Н. В. (т.е. файл подписан). К электронной подписи Клиначёва посредник добавил временную метку и зашифровал пакет своим закрытым ключом. Для подтверждения авторства необходимо самостоятельно вычислить дайджест имеющегося у вас файла и сравнить его с тем, что зашифрован. Расшифровать дайджест можно двумя публичными ключами - посредника и Клиначёва.
Входящий в данный учебно-методический комплекс конспект лекций по своему содержимому наиболее близок к учебнику В. А. Бесекерского, Е. П. Попова "Теория систем автоматического регулирования".
Правом автора Клиначёв Н. В. объявил данный цифровой документ "Свободной информацией". Т.е. пользователям данного документа доступны четыре вида свободы:
Свобода запускать документ в любых целях.
Свобода изучать работу документа и адаптировать его собственным нуждам.
Свобода распространять копии.
Свобода улучшать документ и публиковать свободные
версии.
Однако "Свободная информация" - это не есть "бесплатное пиво". Дабы Вас, как пользователя данного документа нельзя было уличить в воровстве, Вы обязаны соблюдать условия лицензии на свободную документацию и, в зависимости от вашего социального положения, обязаны выполнить следующие действия:
Студент обязан познакомить своего преподавателя с данным документом и сетевыми ресурсами о программе VisSim. В случае если преподаватель не использует в курсе программ для визуального математического моделирования, студент обязан спросить преподавателя, в какой части курса он, за свои деньги, будет ознакомлен с современным инструментарием специалиста в области проектирования систем управления, например, с программой VisSim.
До тех пор пока учебное заведение, в котором работает преподаватель, будет пользоваться "Бесплатной Академической Программой" фирмы Visual Solutions Inc., и не приобретёт у нее полную версию программы VisSim, преподаватель обязан каждые пол года брать счет у фирмы и поднимать вопрос о приобретении программы как на уровне кафедры и факультета, так и на уровне проректора по учебной работе.
Об исследовании точности систем с запаздыванием

Об эффекте квантования параметров
ПФ цифрового PID-регулятора имеет три коэффициента b0, b1, b2. Заметим, что только один коэффициент b1 содержит информацию о таком параметре регулятора как постоянная времени сопрягающего полюса интегрального канала TIx. Для объяснения сути эффекта квантования параметров рассмотрим не усугубляющий случай плотного расположения сопрягающих полюсов. Пусть TIx
= 0,1; TDx = 0,01; при
Tц = 0,0003. Рассчитаем коэффициент b1:

Заметим, что для любой системы отклонение любой постоянной времени в два раза не должно иметь критического значения, однако коэффициенты ПФ-ий, как показано, зависят от параметров отличающихся на порядки, поэтому скажем для отношения TDx/Tц, входящего во все коэффициенты числителя ПФ регулятора требуется сохранять мантиссу длиной 5 знакомест (17 двоичных разрядов), поскольку иначе информация о параметре TIx будет потеряна вследствие округления.
Существуют следующие методы преодоления эффекта квантования параметров при ограниченной длине мантиссы ЦВМ:
Развязка параметров посредствам разложения z-ПФ высокого порядка либо на множители, либо на элементарные дроби.
Подбор для реализации z-ПФ структурной схемы среди альтернативных, имеющих разные по плотности сетки возможных положений корней в единичной окружности.
Обобщенная модель импульсного элемента

Задача идеального импульсного элемента (ИИЭ) в модели - сформировать для дальнейшего математического описания системы либо последовательность импульсов типа d-функций с площадью ~
x(t), либо решетчатую функцию, в основе которой единичная импульсная функция do(t) = { 1 при t=0; 0 при t№0 } с амплитудой ~ x(t).
Задача экстраполятора - математически описать выходную последовательность реального импульсного звена между значениями решетчатой функции (экстраполяция - это прогнозирование (синтез) сигнала по истории выборок вплоть до следующего достоверного значения, которое в текущий момент не известно, и, получив которое, можно провести историческую коррекцию прогноза - интерполяцию).
Коэффициент передачи квантователя (ИИЭ) обратно пропорционален периоду квантования, а коэффициент передачи экстраполятора нулевого порядка равен периоду. Таким образом общий коэффициент передачи квантующей и восстанавливающей цепи, т.е. ИЭ обычно равен единице.
Общая форма записи систем ДУ
В целях формализации процесса составления исходных ДУ систем используют такие методы, как "Метод контурных токов", "Метод узловых потенциалов" и их аналоги, имеющиеся во всех энергетических доменах. В результате их применения получается единая система:
(1)
a11(p) x1 + a12(p) x2 + ... + a1k(p) xk
= f1(t)
a21(p) x1 + a22(p) x2 + ... + a2k(p) xk
= f2(t)
...
ak1(p) x1 + ak2(p) x2 + ... + akk(p) xk
= fk(t)
где:
x1, x2, ..., xk - обобщенные координаты системы, в том числе (для САР) ошибка - x(t)
и регулируемая величина - y(t);
f1(t), f2(t), ..., fk(t) - внешние координаты - задающие g(t) и возмущающие f(t)
воздействия.
Для удобства и формализации решений систему уравнений (1) могут представить в одной из пяти стандартных форм:
в форме Коши;
в пространстве состояний;
решенную относительно регулируемой величины - y(t);
решенную относительно ошибки - x(t);
в виде передаточных функций - W(p), F(p), Fx(p).
Обзор и классификация моделирующих программ
Наблюдается устойчивая тенденция к выравниванию возможностей разных моделирующих программ. Специалист, привыкший к тому или другому пакету не испытывает жесткой потребности в смене программы по причине баланса возможностей. Есть только один причинный критерий, который нужно принимать во внимание при выборе – это технология функционирования математического ядра моделирующей программы. Согласно этому признаку популярные программы сведены в таблицу.
| Программы с поточной моделью управления | ||
| VisSim MBTY Simulink Easy5 |
"+" Эти программы легко интегрируются с системами сбора данных, благодаря чему возможно создание (компьютерных) моделей с физическими объектами в контуре. В большинстве из них возможно программирование цифровых сигнальных процессоров. Структура их моделей может меняться в процессе симуляции без затрат времени, согласно событийному управлению. | |
| Программы – интерпретаторы систем уравнений | ||
| Dynast 20-sim Dymola Simplorer ITI-sim Pspice Multisim Micro-Cap |
"+" Эти программы, в скрытом от пользователя режиме, легко преобразуют текстовую запись систем уравнений к требуемому решателям виду. Фактически с пользователя снята, задача подключения к модели итерационного решателя алгебраических уравнений. Эти особенности технологии позволили не ограничиваться моделями в виде передаточных функций, и, временно, эти программы заняли лидирующие позиции в области мультидоменного моделирования. Они предоставляют пользователю возможность строить модели в виде схем физических принципиальных. | |
Недостатки первой группы моделирующих программ связаны с достоинствами второй и наоборот. Существует технология построения моделей элементов физических устройств с помощью бинаправленных (не направленных) графов связи, которая дает шанс программам первой группы однозначно занять лидирующую позицию.
Главным затруднением для разработчиков моделирующих программ является графический интерфейс, который, по сути, должен быть полноценным редактором векторной графики. По этой причине любая интеграция моделирующих программ с пакетами Visio или CorelDRAW должна приветствоваться пользователями.
Обзор методов анализа моделей, систем и сигналов
В большинстве программ математического моделирования динамических систем совокупность методов анализа моделей, систем и сигналов вынесена в отдельную библиотеку и часто является дополнительным коммерческим продуктом. Их практическая ценность высока. К основным задачам, решаемым библиотекой анализа, относятся:
Идентификация моделей;
Символьный анализ математического описания;
Частотный анализ моделей и систем;
Спектральный анализ сигналов.