Цель работы
Приобретение навыков работы с моделирующими программами VisSim и Electronics Workbench. Ознакомление с этапами моделирования. Определение общих методов представления результатов. Выяснение сути задания параметров симуляции, параметров модели и начальных условий ее энергетического состояния.
Исследование взаимосвязей между параметрами типовых динамических звеньев и их характеристиками. Идентификация реальных технических устройств - схем на операционных усилителях с типовыми звеньями (т.е. с математическим описанием). Приобретение навыков использования типовых возмущающих воздействий и инструментов частотного анализа для исследования систем.
Ознакомление с принципами разомкнутого и замкнутого регулирования. Исследование процессов преобразования сигналов в каналах типового ПИД-регулятора. Изучение свойств непрерывных законов регулирования: пропорционального (П), интегрального (И), изодромного (ПИ) и вариантов с дифференцирующим каналом (ПД, ПИД).
Приобретение навыков использования критериев устойчивости Михайлова и Найквиста. Исследование влияний параметров систем на их устойчивость. Изучение методики применения D-разбиения.
Ознакомление с основными группами критериев качества (оценивающими точность, устойчивость, быстродействие и обобщенные свойства САР). Изучение методики использования интегральных оценок качества при исследовании ошибок систем в типовых режимах движения. Приобретение навыков оценки качества по переходной характеристике и по АЧХ замкнутой системы.
Освоение основных методов повышения точности САР: 1)увеличения коэффициента усиления разомкнутой цепи, 2) регулирования по производным от ошибки с увеличением контурного коэффициента усиления, 3) повышения степени астатизма, 4) применения неединичных обратных связей и масштабирующих устройств на входе / выходе, 5) введения комбинированного управления.
Освоение основных методов повышения запаса устойчивости (коррекции) САР: 1)демпфирования с подавлением высоких частот, 2) демпфирования с подавлением средних частот, 3) демпфирования с подавлением низких частот. Приобретение навыков решения типовых задач коррекции схем на операционных усилителях. Ознакомление с основными видами корректирующих обратных связей: 1) гибкими ООС, 2) жесткими ООС, 3) положительными (изодромное звено на апериодическом звене).
Приобретение навыков использования метода логарифмических частотных характеристик и метода корневых годографов для синтеза САР.
Идентификация влияния временного запаздывания на устойчивость и точностные параметры систем. Ознакомление с различными моделями-аппроксиматорами звена временного запаздывания. Приобретение навыков обоснования применения моделей с допущениями.
Приобретение навыков составления программ для ЦВМ реализующих дискретные передаточные функции. Уяснение технических различий между непосредственным, последовательным и параллельным алгоритмами программной реализации дискретных фильтров.
Предварительное домашнее задание
2.1.Составить уравнения и вывести передаточные функции W(s) для всех блоков файла zvenya.vsm. Сравнить полученные передаточные функции с типовыми, идентифицировать блоки по названиям.
2.1.Составить передаточные функции W(s) для всех блоков структурных схем рабочих файлов.
2.1. По передаточной функции разомкнутой системы (файл mihaylo4.vsm) записать ее характеристический полином D(s), определить его коэффициенты, выделить мнимую и вещественную составляющие.
2.2. Без применения программных инструментов построить асимптотические ЛАЧХ & ЛФЧХ для передаточных функций:
| W(s) = 4 | 0,5s+1 | ; W(s) = 1 | 2s+1 | ; W(s) = 1 | 2s2+s+1 | ||||||
| s2-s | 0,15s+s | s3 |
2.3. Для передаточных функций W(s) (файл nyquist.vsm) вывести передаточные функции соответствующих замкнутых систем Ф(s).
2.4. Самостоятельно познакомиться с сутью итерационных алгоритмов.
Приравнивая в структурной схеме (файл err_ast3.vsm) коэффициенты усиления (KI1 & KI2 & KI3), или (KI2 & KI3) или (KI3) к нулю, можно получить модели САР с астатизмом от нулевого до третьего порядков (считая исходную).
2.1.Начальные значения коэффициентов усиления установить в соответствии с вариантом (см. табл.). Вывести передаточные функции по ошибке Фx(s) для четырех моделей САР при астатизме от нулевого до третьего порядка.
| Вариант | 1 | 2 | 3 | 4 | 5 |
| KI1; KI2; KI3 | 25; 50; 60 | 30; 50; 70 | 35; 50; 80 | 45; 50; 90 | 50; 50; 100 |
2.2. Для тех же моделей вывести формулы расчёта первых четырёх коэффициентов ошибки и определить их числовые значения.
2.3. Описать суть интегральной и улучшенной интегральной оценок качества.
2.4. Составить функцию цены из блоков пакета VisSim, подсчитывающую количество переходов через ноль ошибки САР в переходном процессе.
2.1. Дано пять систем. Каждая обладает совокупностью уникальных свойств (см. табл.). В работе изучается пять методов повышения точности САР. Выбрать наиболее эффективный или единственно возможный метод повышения точности для каждой САР. Выбор обосновать.
| Nо |
Свойства САР (состоящих из минимально фазовых звеньев) |
Метод, файл |
| 1 | САР статическая. Контурный коэффициент мал (<10). Объект и чувствительный элемент являются одним конструктивным элементом (нет возможности изменить вид ЛАЧХ прямого канала) | |
| ИЛИ: ЛАЧХ разомкнутой системы в области низких частот имеет наклон -20 или -40 дб/дек. При этом либо в измерительном канале (на входе, вне контура регулирования) неединичный коэффициент передачи, либо в цепи обратной связи установлен делитель сигнала | ||
| 2 | Объект моделируется двумя звеньями: колебательным (с большим подавлением) и апериодическим. Сопрягающая частота апериодического звена на две декады меньше резонансной частоты колебательного звена | |
| 3 | ЛАЧХ разомкнутой системы имеет вид 20-0-20-40 (участок с нулевым наклоном не продолжителен). Предъявлены требования: минимально возможное перерегулирование, и малые собственные шумы САР. В точке единичного усиления фаза, уменьшаясь, пересекает значение -90 градусов с небольшим приращением | |
| 4 | Объект моделируется двумя звеньями: колебательным (с большим подавлением) и апериодическим. Сопрягающая частота апериодического звена на две декады больше резонансной частоты колебательного звена | |
| 5 | ЛАЧХ разомкнутой системы в области низких частот имеет наклон 0 дб/дек. Контурный коэффициент объекта не стабилен в той же полосе частот (в области низких частот); или предъявлено требование равенства нулю первой или первой и второй составляющих ошибки |
2.1. Дано четыре системы. Каждая обладает совокупностью уникальных свойств (см. табл.). Подобрать наиболее оптимальное или единственно возможное, последовательное корректирующее звено для каждой САР (апериодическое, пассивное дифференцирующее, пассивное интегрирующее, пассивное интегро-дифференцирующее). Выбор обосновать.
| Nо |
Свойства САР (состоящих из минимально фазовых звеньев) |
метод, звено, файл |
| 1 | ЛФЧХ разомкнутой системы чуть ниже частоты среза (в пределах декады) меняет свое значение от -90 до -270 градусов. Допустима минимально возможная потеря частотных свойств (площади ограниченной ЛАЧХ и осью частот) | |
| 2 | ЛАЧХ разомкнутой САР соответствует трехкаскадному операционному усилителю без внутренней коррекции (звено с большим коэффициентом усиления и три апериодических звена с близкими сопрягающими частотами), и пересекает ось частот с наклоном -60 дб/дек. Допустима существенная потеря полосы пропускания | |
| 3 | ЛФЧХ системы вплоть до частоты среза приобретает значения около -180 градусов. Для исключения условий, при которых возможно появление неустойчивости в большом, дополнительные отрицательные фазовые сдвиги не допустимы | |
| 4 | Вблизи частоты среза и ниже по частоте более декады наклон ЛАЧХ разомкнутой системы составляет -40 дб/дек. Допустима минимально возможная потеря частотных свойств |
2.2. Составить структурную схему и построить ЛАЧХ & ЛФЧХ для передаточной функции корректирующего звена: W(s)=1/(1+T1s)+(0,1)+T2s/(1+T2s);
T1=0,1; T2=0,0001. Определиться с его названием. Разобраться, какие изменения в структурной схеме звена надо сделать, чтобы получить: апериодическое, или пассивное дифференцирующее или пассивное интегрирующее звено.
2.1.В соответствии с вариантом (см. табл.) построить располагаемую ЛАЧХ объекта регулирования. Учитывая требования к точности и к устойчивости, нанести на график низкочастотную и высокочастотную запретные области.
| Параметры |
Значения |
Вариант | |||||||
| Располагаемая передаточная функция объекта |
|
1, 2 | |||||||
|
3, 4 | ||||||||
| Требования к точности |
Vm =10 ед./с; Em = 100 ед./с2; Xm =0,01 ед. | 1, 3 | |||||||
| wK = 0,3 рад/с; Dj = 0,573e-3 град; d = 9e-6 % |
2, 4 | ||||||||
| к устойчивости | M < 1,16 | 1,2,3,4 |
2.2. Определить передаточные функции последовательных (возможно последовательно-параллельных) корректирующих устройств, которые рекомендуется разбить на типовые звенья. Составить структурную схему системы с устройствами коррекции.
2.1. Рассчитать критическое запаздывание для системы (файл e^(-st)2.vsm) (по вариантам).
2.2. Построить асимптотические ЛАЧХ & ЛФЧХ для звена с передаточной функцией W(s)=(1-Ts)/(1+Ts).
2.1. Выбрать язык программирования для выполнения лабораторной работы - Pascal или Си++. Ознакомится с технологией создания внешних dll-моделей для моделирующей программы VisSim (см. прил. 1, 2).
2.2. Адаптировать предложенный шаблон программы для реализации рекурсивного цифрового фильтра второго порядка. По умолчанию можно выбрать произвольные значения для коэффициентов фильтра, но они должны быть доступны для изменения пользователем. Фильтр должен иметь дополнительный вход для сигнала синхронизации выполнения программы. Если номер варианта 1, 2, 5, 6, ..., то нужно воспользоваться непосредственным алгоритмом с одним буфером; если - 3, 4, 7, 8, ..., то тем же алгоритмом, но с двумя буферами (см. рис. 1, 2).
Содержание работы
2.1.Выяснить порядок запуска используемых программных пакетов VisSim и Electronics Workbench.
2.2. Ознакомиться с демонстрационным роликом о работе с программой VisSim (при наличии доступа к файлу csd_new.scm -
download "control system design demo"). Преподаватель может организовать собственную демонстрацию для студентов. Выявить: а) назначение программы, б) основные этапы работы с программой.
2.3. Запустить программу VisSim. Загрузить файл rlc.vsm. Записать соответствующую блок-схеме систему уравнений. Выполнить сравнение уравнений модели с формами записи закона Ома для "R", "L" и "C"-элементов. Предложить схемы электрических цепей, которые описываются данной системой уравнений. Идентифицировать на чертеже блок-схемы параметры моделируемых элементов и выяснить начальные условия в схеме. Изучить характер влияния параметров, а за тем и начальных условий на вид переходного процесса.
2.4. Запустить программу Electronics Workbench. Загрузить файл rlc.ca4. Изменить начальные условия и параметры модели по собственному усмотрению (ваш отчет будет уникальным). Вновь загрузить файл rlc.vsm с начальными настройками. Изменить их таким образом, чтобы переходные процессы в VisSim'е совпали с соответствующими в Electronics Workbench'е.
2.5. По вариантам (см. табл.) спроектировать модели источников периодического сигнала в пакете VisSim. Измерить, и, при необходимости, компенсировать постоянную составляющую в сигнале. Использовать блок plot
для осциллографирования.
| Вариант | Форма сигнала | Частота, кГц | Амплитуда, ед. |
| 1 | Прямоугольный скважность 1:2 | 10 | 10 |
| 2 | Треугольный | 20 | 20 |
| 3 | Линейно нарастающий | 30 | 30 |
| 4 | Нарастающий по параболе | 40 | 40 |
| 5 | Модуль синусоиды | 50 | 50 |
Методические указания к моделированию и рекомендации к содержанию отчета
3.1. Кратко описать отличие в принципе функционирования программ VisSim и Electronics Workbench от математических пакетов подобных Mathcad'у.
3.2. Привести распечатки, подтверждающие выполнение всех пунктов экспериментальной части и текстовые пояснения к ним.
3.3. При изучении характера влияния параметров на вид переходного процесса не следует менять их одновременно (см. пп. 2.3). Проверьте тенденции при вариации одного, произвольно выбранного параметра. Такой же подход необходим при изучении характера влияния начальных условий на вид переходного процесса.
3.4. Для измерения постоянной составляющей (см. пп. 2.5) следует составить блок-схему соответствующую магнитоэлектрическому измерительному механизму, который реагирует на среднее значение. Главный блок в модели измерительного преобразователя - интегратор.
3.5. Выводы.
Содержание работы
3.1. В программе VisSim ознакомиться с моделями единичной ступенчатой функции - 1(t) и дельта-функции - 1'(t) (файл zvenya.vsm). Выявить положенные допущения (неидеальности) в моделях.
3.2. В программе VisSim (файл zvenya.vsm) выполнить исследование типовых динамических звеньев (см. п. "Методические указания к моделированию и рекомендации к содержанию отчета"). По ходу работы необходимо изменить постоянные времени, коэффициенты затухания и усиления по своему усмотрению. Убедится, что дифференцирование переходной функции звена - h(t) дает его функцию веса - w(t); и наоборот, интегрирование функции веса звена - w(t) дает его переходную функцию - h(t).
3.3. Выполнить измерения виртуальными приборами (анализатор, осциллограф) в схемах на операционных усилителях (файлы *.ca4 для программы Electronics Workbench) с целью идентификации моделей с типовыми динамическими звеньями. Настроить схемы по совпадению вида ЛАЧХ & ЛФЧХ, а так же реакций подобных переходной функции и функции веса. Допустимо несовпадение только коэффициентов усиления.
3.4. Подавая на вход типовых динамических звеньев синусоидальный сигнал, убедиться, что изменение коэффициента усиления вне полосы пропускания за одну декаду составляет либо 20 дб (10 раз), либо 40 дб (100 раз).
3.1. Изучить параметры сигнала задания g(t) в файле open.vsm. ( определить интервалы, где координата задания постоянна, меняется с постоянной скоростью или с постоянным ускорением).
3.2. Включая каналы типового ПИД-регулятора по очереди, изучить, как формируется сигнал воздействия на объект - u(t) из первичной информации - x(t) (файл open.vsm).
3.3. В файлах open.vsm и closed.vsm коэффициенты усиления регуляторов оптимально настроены для управления объектом в соответствии с принципами Понселе (без ОС) и Ползунова-Уатта (с ОС). По своему усмотрению изменить параметры объекта и вновь настроить регуляторы.
3.4. Оценить степень влияния изменений параметров объекта на ошибку регулирования для обоих вариантов управления. При анализе следует учесть, что статическую составляющую ошибки определяет нестабильность коэффициента усиления объекта, а динамическую - его постоянная времени.
3.5. Изучить реализацию ПИД-регулятора на ОУ (файл pid.ca4).
3.1.Исследовать границу устойчивости (типы границы устойчивости), используя возможность пакета VisSim задать передаточную функцию с помощью перечисления корней (нулей и полюсов её числителя и знаменателя). Убедиться, что только корни-полюсы с неотрицательной вещественной частью приводят к расходящемуся переходному процессу.
3.2. Исследовать влияние корней характеристического полинома на вид годографа Михайлова (файл mihaylo4.vsm).
3.3. Изучить влияние контурного коэффициента усиления на устойчивость системы и вид годографа Михайлова.
3.4. Задавая постоянную времени T2 по варианту (см. табл.), подбором найти коэффициент усиления системы, при котором она будет находиться на колебательной границе устойчивости. В качестве признака границы использовать критерий Михайлова.
| Вариант | 1 | 2 | 3 | 4 | 5 |
| T2 | 0,12; 0,42; 0,72 | 0,18; 0,48; 0,78 | 0,24; 0,54; 0,84 | 0,30; 0,60; 0,90 | 0,36; 0,66; 0,96 |
3.5. Познакомиться с применением D-разбиения (файл d_4_k&t.vsm). Убедиться, что параметры, см. пп. 3.4, образуют точки на границе разбиения. Определить частоты для этих точек.
3.6. Исследовать на устойчивость передаточные функции, предложенные в файле nyquist.vsm, применяя годограф Найквиста и логарифмические частотные характеристики.
3.7. Изучить характер влияния контурного коэффициента усиления на устойчивость и на полосу пропускания замкнутой системы - модели электронного усилителя на трехкаскадном ОУ (файлы ou3.vsm и ou2+1.ca4). Менять контурный коэффициент усиления предполагается делителем в цепи обратной связи.
3.1. Изучить сигнал задания g(t) спроектированный для введения систем в режимы типового движения (файл err_ast3.vsm). Заполнить таблицу.
| Временной промежуток постоянства параметров сигнала | |||||
| Параметр сигнала и его значение |
3.2. Измерить значения первых четырех установившихся ошибок по: положению q0, скорости
qu, ускорению qe, и приращению ускорения qg''' для систем с астатизмом от нулевого до третьего порядков (файл err_ast3.vsm). Параметры моделей должны соответствовать расчетному заданию. Опираясь на экспериментальные данные определить коэффициент усиления систем в области низких частот K, а так же добротности по скорости Ku, ускорению Ke и приращению ускорения Kg'''. Определить численные значения коэффициентов ошибок по положению, скорости, ускорению и приращению ускорения -
c0, c1, c2, c3. Заполнить таблицу.
| Система \ Ошибки | q0 & K & c0 |
qu & Ku & c1 |
qe & Ke & c2 |
qg''' & Kg''' & c3 |
| W(s)=1/s^0 * ... | ||||
| W(s)=1/s^1 * ... | ||||
| W(s)=1/s^2 * ... | ||||
| W(s)=1/s^3 * ... |
3.3. Изучить влияние (качественно) на вид переходной функции h(t) систем с астатизмом первого второго (и третьего по указанию преподавателя) порядков возмущающего воздействия f(t). В качестве f(t) использовать сигнал задания g(t) спроектированный для изучения типовых режимов движения систем. Возмущающее воздействие подавать до и после интегрирующих элементов, менять его знак и подбирать амплитуду так, чтобы ошибка от возмущения в установившемся режиме составляла 10...30 % от h(t) и была наглядна при визуальном наблюдении (информацию удобно представить в режиме перекрытия графиков).
3.4. Минимум три раза оптимально настроить ПИД-регулятор для модели системы регулирования (файл err_s^-1.vsm), используя разные функции цены - интегральные оценки качества.
3.1.Ознакомиться с предложенными моделями, идентифицировать их с описаниями в таблице.
3.2. Определить цель применения изучаемых методов повышения точности для каждой модели (повышение точности в установившихся режимах, увеличение запаса устойчивости или повышение быстродействия).
3.3. Повысить точность систем в соответствии с выбранными методами.
3.4. Качественно описать результаты применения методов повышения точности. Рекомендуется использовать переходную функцию h(t). Графическую информацию удобно представить в режиме наложения (перекрытия) результатов моделирования.
3.5. Используя инструменты частотного исследования систем (ЛАЧХ & ЛФЧХ) сформулировать ограничения в применении каждого метода повышения точности.
3.6. Выполнить количественное исследование результатов применения методов повышения точности САР на основе исследований (измерений) ошибки x(t). Можно измерить значения первых установившихся составляющих ошибки по: положению q0, скорости qu, ... - до и после применения методов повышения точности. По необходимости рекомендуется использовать тест-сигналы задания g(t): единичную ступенчатую функцию 1(t), синусоидальный, меняющийся с постоянной скоростью или ускорением (см. сигнал g(t) в файле err_ast3.vsm). Для измерений ошибки рекомендуется использовать: датчики скорости и ускорения (дифференцирующие звенья), преобразователи построенные в соответствии с интегральными оценками качества, а так же измерители действующего или средневыпрямленного значений (см. файл rms_ex.vsm). Выбор схемы измерения ошибки x(t) следует обосновать.
3.7. Рассмотреть все блоки (звенья), которые применялись для повышения точности. Назвать техническое устройство их практической реализации. Рассмотрев все модифицированные модели САР, указать необходимые диапазоны для подстраиваемых параметров этого устройства.
3.1.Ознакомиться с первыми четырьмя предложенными моделями систем, идентифицировать их с описаниями в таблице. Изменить параметры моделей так, чтобы их логарифмические частотные характеристики сместились вдоль частотной шкалы.
3.2. Скорректировать системы в соответствии с выбранными методами (ввести соответствующие корректирующие звенья в контур и настроить их, добиваясь устойчивости в замкнутом состоянии).
3.3. Дать количественную характеристику результатам коррекции, оценивая: полученный запас устойчивости (L & m
или M), потери точности (K или Ku
или Ke), и уменьшение быстродействия (wП, wС).
3.4. По указанию преподавателя, для одной из исследуемых моделей составить подобную на операционных усилителях в пакете Electronics Workbench. Рекомендуется использовать модели из лаб. раб. №2. Смотри так же рабочий файл "функциональные устройства на ОУ".
3.5. Изучить модели *.ca4, в которых рассмотрены стандартные задачи коррекции схем на операционных усилителях. Описать суть способов коррекции. Дать количественную характеристику результатам, оценивая их аналогично пп. 3.3.
3.6. В соответствии с вариантом (см. табл.), составить подобную схеме на операционном усилителе модель из блоков пакета VisSim.
| Вариант, модель |
Описание типовых задач коррекции схем на ОУ |
| 1 kor_ou3.ca4 |
Выходное сопротивление ОУ и паразитная емкость монтажа выходных цепей образуют третий полюс ЛАЧХ, ведущий к неустойчивости. Модель можно рассматривать как схему на трехкаскадном ОУ без или с частичной внутренней коррекцией |
| 2 kor_c_in.ca4 |
Паразитная емкость монтажа входных цепей ОУ и большое сопротивление обратной связи образуют апериодическое звено первого порядка, которое может привести к неустойчивости схем на ОУ |
| 3 kor_cout.ca4 |
Необходимость работы ОУ на емкостную нагрузку приводит к тому, что выходное сопротивление ОУ и емкость нагрузки образуют третий полюс ЛАЧХ, ведущий к неустойчивости. Малое сопротивление емкости нагрузки на высоких частотах может перегрузить выход ОУ |
| 4 kor_2_ou.ca4 |
Стремление получить в схемах высокую точность и быстродействие приводит к необходимости использования двух ОУ (точного и быстродействующего). Но простое последовательное включение приводит к неустойчивости схемы, поскольку минимальное фазовое запаздывание для двух, даже корректированных ОУ составляет 180 градусов |
| 5 kor_derv.ca4 |
Построение дифференциатора на ОУ вызывает затруднения: а) в петле ОС ОУ оказывается включенным апериодическое звено с большой постоянной времени, что увеличивает результирующее запаздывание по фазе свыше значения 180 градусов и приводит к неустойчивости схемы; б) входное емкостное сопротивление дифференциатора может вызвать неустойчивость и в предыдущем каскаде на ОУ; в) коэффициент усиления схемы по высокой частоте велик и это ухудшает соотношение сигнал/шум |
3.7. Ознакомиться с тремя наиболее часто используемыми видами корректирующих обратных связей (файл kor_ooc.vsm). Определить, какими последовательными корректирующими звеньями можно добиться тех же результатов.
3.1. Дополнить структурные схемы в рабочих файлах рассчитанными последовательными корректирующими звеньями. Проверить, имеет ли ЛАЧХ системы желаемый вид.
3.2. Пустые блоки "1" и "2" определяют места возможного подключения средств коррекции к реальной системе. Заменить часть последовательных корректирующих устройств эквивалентной обратной связью, в соответствии с заданной структурой системы.
3.3. Точно настроить устройства коррекции и выполнить измерения, подтверждающие верность результатов синтеза, подавая тест сигналы с необходимыми параметрами.
3.4. Используя корневой годограф, определить параметр затухания z для сопряженных комплексных корней передаточной функции синтезированной системы при единичной обратной связи. А также определить во сколько раз должен увеличиться контурный коэффициент усиления (добротность по скорости), чтобы система оказалась на границе устойчивости (проверить по переходной функции).
3.1. Ознакомиться с процессом симуляции в звене временного запаздывания, построенном на буфере (блок "timeDelay"). Изучить структурное построение двух предложенных линеаризовананных моделей-аппроксиматоров звена временного запаздывания (файл e^(-st).vsm).
3.2. Оценить адекватность получаемых результатов при использовании каждой из трех альтернатив звена в моделях систем, если ставятся задачи: а) симуляции движения (файл e^(-st).vsm); б) оценки точности (файл e^(-st)2.vsm); в) оценки запаса устойчивости (файл e^(-st)2.vsm).
Изучаемая методика построения цифровых регуляторов или устройств коррекции предполагает переход к дискретным реализациям от непрерывных аналогов. Нечетные варианты должны реализовать цифровой ПИД-регулятор (файл err_s^-1.vsm), четные - цифровое корректирующее устройство (файл k3.vsm). Далее по тексту для четных вариантов вместо названия "ПИД-регулятор" следует читать "корректирующее устройство".
3.1. В рабочем файле *.vsm настроить ПИД-регулятор определив качественные показатели по своему усмотрению. Изменить параметры системы так, чтобы ЛАЧХ & ЛФЧХ сместились вдоль частотной шкалы в пределах двух декад.
3.2. Заменить структурную схему ПИД-регулятора одним блоком "transferFunction" с эквивалентными параметрами. Проконтролировать неизменность переходного процесса.
3.3. Несколько раз осуществить переход от непрерывной передаточной функции ПИД-регулятора (transferFunction) к дискретной, отыскивая наибольший период дискретизации, при котором качество переходного процесса не ухудшается значительно.
3.4. Перенести коэффициенты дискретной передаточной функции регулятора в подготовленный текст программы, выполнить её компиляцию и подключить полученную динамически загружаемую библиотеку (файл *.dll) к рабочему файлу посредствам блока "userFunction". Убедиться в схожести переходного процесса.
3.5. Разложить дискретную передаточную функцию регулятора на множители и на элементарные дроби, для написания разделённых программ в соответствии с последовательным и параллельным алгоритмами. В соответствии с этими алгоритмами в рабочем файле регулятор должен состоять из блоков "userFunction" включенных последовательно или параллельно.
Методические указания к моделированию и рекомендации к содержанию отчета
4.1. Привести названия и графики использованных типовых возмущающих воздействий. Описать изменения в реакции типовых звеньев на варьирование параметров воздействий.
4.2. Для каждого звена привести: а) название звена; б) структурную схему (подписав входную величину, выходную, сигнал ошибки и обратной связи); в) вывод передаточной функции (подставить коэффициенты усиления и постоянные времени; проверить соответствие с линеаризованной передаточной функцией, которую рассчитывает программа VisSim (Analyze, Transfer Function Info); записать координаты корней и полюсов функции); г) список параметров с описанием характера влияния (на ЛАЧХ & ЛФЧХ, переходные процессы, ...); д) переходную функцию; е) функцию веса; ж) ЛАЧХ & ЛФЧХ (определить достигает ли фаза значения -180 градусов в диапазоне частот и если да, то имеет ли звено на данной частоте коэффициент усиления больший единицы); з) диаграмму Найквиста (определить охватывает ли АФХ точку (-1, j0); отметить траектории для положительных и отрицательных частот; точки, в которых частота стремится к нулю и к бесконечности); и) корневой годограф (определить имеются ли нулевой, положительные, или чисто мнимые корни; если есть парные корни с мнимой частью, то по мнимой части определить собственную частоту колебаний звена и сравнить с колебаниями переходной функции или функции веса, сделать вывод об устойчивости звеньев).
4.3. Указать на неидеальности, присущие свойствам, которыми обладают реальные дифференцирующие устройства и их компьютерные дискретные модели. Пояснить причину неидеальности в дискретных моделях.
4.4. Кроме осциллограмм, ЛАЧХ & ЛФЧХ подтверждающих результаты настройки схем по пп. 3.3 необходимо привести схемы проведения измерений (включая источники тест-сигналов) и дать пояснения к ним.
4.1. Привести общее описание типового ПИД-регулятора ( структурная схема, дифференциальное уравнение или передаточная функция, основные параметры).
4.2. Описать принципиальные отличия в формировании сигнала воздействия на объект u(t) каналами типового ПИД-регулятора (сравнительный анализ): а) при малых возмущениях в первичной информации x(t), и при больших; б) при постоянстве входной координаты, при движении её с постоянной скоростью и с постоянным ускорением. Привести поясняющие графические зависимости.
4.3. Привести переходные процессы: а) при оптимальных настройках регуляторов для разных принципов регулирования объектом; б) для тех же случаев, с теми же настройками, но при отклонениях параметров объекта. Дать пояснения.
4.4. Построить два семейства зависимостей приведенной статической погрешности от изменения коэффициента усиления объекта при разных коэффициентах передачи пропорционального канала регулятора. В первом случае - для управления с ОС, во втором - без ОС. Первое семейство погрешностей привести к сигналу задания 1(t), второе - к среднему значению коэффициента усиления для каждой вариации (семейство вырождается в один график). Пояснить результаты.
4.5. Определить для модели ПИД-регулятора на ОУ коэффициенты усиления каждого канала. Для интегрального и дифференциального каналов необходимо указать граничные (сопрягающие) частоты или соответствующие постоянные времени. Нанести значения параметров на ЛАЧХ & ЛФЧХ регулятора. Выявить соответствие между параметрами и элементами схемы. Описать, какие ограничения накладывает частотная характеристика типового ОУ на параметры ПИД-регулятора. Продемонстрировать изменения сдвига фаз сигналов на характерных участках частотных характеристик, используя сигнал синусоидальной формы. При выполнении экспериментов следует учитывать, что данный ПИД-регулятор инвертирует сигнал.
4.1. Для произвольно спроектированных передаточных функций привести переходные процессы, соответствующие наличию: а) одного и двух нулевых корней-полюсов; б) паре чисто мнимых корней-полюсов; в) корню-полюсу с положительной вещественной частью.
4.2. Убедиться, что каждый корень-полюс с отрицательной вещественной частью разворачивает годограф Михайлова на 90 градусов против часовой стрелки, а с положительной - на 90 градусов по часовой.
4.3. Продемонстрировать влияние коэффициента усиления на вид переходных процессов и вид годографа Михайлова (в режиме перекрытия графиков).
4.4. Для D-разбиения, указать область устойчивости (подтвердить моделированием) и выяснить влияние параметров на ее размер.
4.5. Среди предложенных к изучению с помощью годографа Найквиста и логарифмических частотных характеристик найти передаточные функции, отвечающие следующим признакам: а) астатические (указать порядок); б) имеющие корни-полюсы с положительной вещественной частью (Transfer Function Info); б) неустойчивые в разомкнутом состоянии; в) неустойчивые в замкнутом состоянии; ж) в которых понижение коэффициента усиления приведет к появлению неустойчивости в замкнутом состоянии; з) в которых повышение коэффициента усиления приведет к появлению неустойчивости в замкнутом состоянии; д) условно устойчивые; г) абсолютно устойчивые. Результаты свести в таблицу с отметками "+" и "-". Методика получения результатов должна быть отображена.
4.6. Пункт 3.7 предполагает построение семейств ЛАЧХ & ЛФЧХ для разомкнутой и замкнутой систем, при варьировании контурного коэффициента усиления электронного усилителя. Для замкнутой системы дополнительно требуется получить семейство переходных характеристик. Кроме пояснения графических результатов, в отчете привести описание модели трехкаскадного ОУ. Модель для пакета Electronics Workbench (ou2+1.ca4) предполагается использовать для сравнительного контроля полученных результатов.
4.7. Описать с точки зрения удобства применения в исследованиях годографы Михайлова, Найквиста и ЛАЧХ.
4.1. Исследование точности в типовых режимах (пп. 3.1, 3.2, 3.3) следует проиллюстрировать временными зависимостями с подробными пояснениями. Внесенные в таблицы данные, должны быть отражены на графиках. Рекомендуется использовать режим графического наложения результатов моделирования при изменении знака и точки ввода воздействий.
4.2. Сравнить экспериментальные значения коэффициентов ошибки с расчетными.
4.3. В основе функций цены для итерационного процесса оптимизации должны быть: интегральная оценка качества; улучшенная интегральная оценка; и оценка дополнительно использующая параметры переходного процесса - перерегулирование или количество колебаний. Сравнить эффективность оценок, качественно характеризуя принципиально достижимые результаты.
4.4. Показатели качества найденные в пп. 3.5 и 3.7, нанести на переходные характеристики h(t), АЧХ замкнутой системы |Ф(jw)|, АФХ и ЛАЧХ & ЛФЧХ разомкнутой системы соответственно. Сравнить качество настроек ПИД-регулятора в трех случаях. АЧХ замкнутой системы |Ф(jw)| - это ее ЛАЧХ, у которой ось модуля не логарифмическая (снимите соответствующую галочку в свойствах графика). При определении ЛАЧХ & ЛФЧХ разомкнутой системы следует выделить требуемые блоки структурной схемы и отметить точки входа и выхода сигнала (Select Input/Output Points).
4.1. Готовые звенья для изменений в структурных схемах моделей находятся в блоке Instruments. Только требуемое звено и соответствующий регулятор настройки нужно перенести и подключить к модели. Изменения в структурных схемах отразить в отчете.
4.2. Если моделирование занимает много времени (10...20 с, VisSim 1.2), то отключите второстепенные визуализирующие приборы - такие как блок Display. Синхронный с разверткой вывод на экран информации на каждом шаге расчёта растягивает последний на 1/50 секунды.
4.3. В случае применения неединичных обратных связей или масштабирующих устройств на входе / выходе или комбинированного управления использование выходного сигнала чувствительного элемента системы (сумматора) для исследования ошибки x(t) не имеет смысла. Необходимо вычесть выходной сигнал y(t) из входного g(t) дополнительным сумматором.
4.1. Определить ЛАЧХ & ЛФЧХ разомкнутой системы в пакете VisSim можно без размыкания контура - необходимо выделить все блоки файла, а за тем отменить выделение только для источника сигнала и сумматора. Если САР неустойчива, то нужно разорвать контур. Для описанного выделения выполните два действия: а) установите мышь на свободное место и нажмите Shift+[правая клавиша мыши] (выделение всей схемы), б) повторная отметка указанной комбинацией любого элемента схемы отменит выделение для него. В некоторых случаях потребуется принудительно отметить вход и выход. Далее - стандартно.
4.2. При составлении моделей по пп. 3.4, допускается произвольная инверсия сигналов в схемах на операционных усилителях, но следует обратить внимание на результирующий фазовый сдвиг от инверсии.
4.3. Схемотехника инвертирующих включений операционных усилителей предполагает введение входного сигнала в корректирующую цепь. Если при построении моделей в пакете VisSim по пп. 3.6 это вызывает затруднения, то можно перейти к неинвертирующему включению операционного усилителя.
4.4. В пакете Electronics Workbench методика использования виртуального прибора - анализатора сильно упрощена. На практике, подобные подключения прибора не позволят снять частотную характеристику операционного усилителя с разорванной обратной связью. Дайте пояснения.
4.5. В файле kor_ooc.vsm корректирующие обратные связи должны включатся не одновременно.
4.1. При синтезе низкочастотных корректирующих устройств следует полагать, что подъём ЛАЧХ от запретной области не допустим, по причине возможного возрастания влияния помех и наводок на входе.
4.2. При выполнении измерений, цель которых - определить точность замкнутой системы, следует подавать синусоидальные сигналы как на участках границы запретной области с разным наклоном, так и на сопрягающей частоте. Только фазовую ошибку Dj допустимо измерить, прибегая к функциям частотного анализа (необходимо задаваться очень узким частотным диапазоном).
4.3. При точной настройке системы по показателю колебательности M следует помнить, что второй пик АЧХ замкнутой системы |Ф(jw)| так же не должен достигать уровня M.
4.4. Для построения годографа корней в пакете VisSim нужно выделять разомкнутую систему W(s).
4.5. VisSim строит годограф корней - 1+KocW(s)=0 - характеристического уравнения замкнутой системы Ф(s) с варьируемым коэффициентом передачи в цепи обратной связи Koc, для выделенных блоков, которые принимает за разомкнутую систему W(s):
Если Koc=0, то корни уравнения 1+KocW(s)=0 устремляются к корням-полюсам W(s), которые отмечены крестами (только при Koc=0!).
Если Kос стремится к бесконечности, то часть корней уравнения 1+KocW(s)=0 устремляется к корням-нулям W(s), а часть - к бесконечности.
Если Koc=1, то характеристическое уравнение соответствует единичной обратной связи.
4.6. Если уточнять координаты корней на траекториях годографов, то дополнительно будут высвечиваться три соответствующие корню параметра: 1) Koc; 2) параметр затухания - z
(в программе VisSim - z); 3) угловая частота свободных колебаний -
w. По значению Koc, можно оценить: при каких значениях контурного коэффициента усиления K*Koc система станет не устойчивой, а также быстродействие системы. Степень быстродействия определяется по самому ближнему к мнимой оси корню на траекториях при заданном значении Koc. Параметр затухания - z
и угловую частоту свободных колебаний - w легко интерпретировать, если вспомнить, что передаточная функция замкнутой системы с комплексными корнями Ф(s) часто может быть аппроксимирована колебательным звеном.
4.1. При использовании линеаризованных моделей- аппроксиматоров звена временного запаздывания наиболее схожими переходные процессы будут в случае использования простейших методов интегрирования - Эйлера, и трапециидального. В пакете VisSim все функции анализа для блока "timeDelay" не доступны.
4.2. Выполняя пункт 3.1, следует назвать звенья составляющие модели-аппроксиматоры звена временного запаздывания и указать, каким образом следует изменить их структуру для более точной аппроксимации.
4.3. Оценить адекватность симуляции движения (пп. 3.2.а) необходимо исходя из положений: а) сигнал на входе системы имеет широкий спектр (может меняться с большими скоростями и ускорениями); б) сигнал на входе звена, в силу инерционных свойств системы, имеет ограниченный спектр.
4.4. Оценить адекватность результатов при исследовании точностных параметров систем (пп. 3.2.б) необходимо для двух методик. Первая предполагает измерение ошибок в типовых режимах движения (см. л.р. No 5). Вторая - изучение параметров ЛАЧХ в области низких частот (см. л.р. No 8).
4.5. Оценить адекватность результатов при исследовании запасов устойчивости систем (определении критического запаздывания), (пп. 3.2.в) необходимо для двух методик. Первая предполагает подбор запаздывания при симуляции движения до получения переходного процесса соответствующего границе устойчивости. Вторая базируется на изучении частотных свойств разомкнутой системы в области частоты среза либо по ЛАЧХ & ЛФЧХ, либо по АФХ (годограф Найквиста).
4.6. Выводы по работе должны содержать рекомендации о том, каким из аналогов звена временного запаздывания наиболее целесообразно пользоваться и для каких целей.
4.1. При выполнении работы рекомендуется использовать простейший метод интегрирования - Эйлера.
4.2. При настройке ПИД-регулятора рекомендуется убедиться в отсутствии комплексных нулей у его передаточной функции. Если таковые имеются, следует поднять коэффициент в пропорциональном канале.
4.3. Получить коэффициенты полиномов числителя и знаменателя, а также значения их корней для выделенной части структурной схемы можно воспользовавшись пунктами меню "Analyze", "Transfer Function Info".
4.4. Для осуществления перехода от непрерывной передаточной функции к дискретной, на вкладке свойств блока "transferFunction" следует нажать кнопку "Convert S->Z" и ввести период дискретизации больший, чем шаг моделирования.
4.5. При манипуляциях с коэффициентами полиномов числителя и знаменателя дискретных фильтров следует воздержаться от округлений - переход от изображения Лапласа к Z-изображению описывается свертыванием правой полуплоскости "устойчивых" корней в несравнимо малую окружность единичного радиуса, т.е. точность позиционирования корня должна быть эквивалентно выше.
4.6. Разложение на множители и на элементарные дроби не обязательно выполнять для дискретной передаточной функции, можно выполнить его и для непрерывной, а потом уже перейти к дискретным фильтрам первого порядка. При этом возможности пакета VisSim освобождают от расчетов.
4.7. Для выявления других технических особенностей каждого из трех алгоритмов следует попытаться идентифицировать частотные свойства для разделенных блоков, составляющих ПИД-регулятор (см. пп. 3.5) и выявить параметры, которые отвечают за его настройки.
Аккумулирующий (материю) узел
Структурная схема аккумулирующего узла существенно проще (см. рис.) и особых комментариев не требует.

Активные элементы ненаправленного графа (источники энергии)
Источники энергий определяют само существование энергетических доменов. В разных энергетических доменах нам известно разное количество источников. Функционирование известных нам источников может быть описано одной из двух идеализированных моделей. Первая модель имеет название "Источник движущей силы", поскольку в рабочем режиме создает разность энергетических потенциалов неизменной величины. Вторая модель– "Источник потока" – отличается тем, что генерирует постоянный по величине поток материи (рабочего тела).
Алгоритмы идентификации частотных характеристик систем на основе технологий распознавания образов
Идея алгоритмов идентификации ЧХ систем на основе технологий распознавания образов заключена в уточнении априорных предположений о порядке системы и порядке её астатизма. Согласно сценарию, алгоритм создает образ идентифицируемой системы (модель), и, в итерационном процессе, так подгоняет положение асимптот его частотной характеристики, дабы реакции идентифицируемой системы и образа на произвольные сигналы совпадали.
Простейшие алгоритмы данной группы обеспечивают погрешности идентификации не превышающие трети декады и 6 дБ, что вполне приемлемо при проектировании систем управления. В целях снижения погрешностей для идентификации выбирают фрагменты осциллограмм сигналов с наиболее широким спектром (переходные режимы функционирования).
Безусловно, группа измерительных алгоритмов в любых случаях более предпочтительна. Но в условиях, когда возможность вывода системы из производственного процесса для исследований отсутствует, или же невозможно подать на систему требуемые измерительные воздействия выбора нет – нужно использовать те сигналы, которые есть.
Алгоритмы программ цифровых фильтров
Существует три основных алгоритма программной реализации дискретных передаточных функций (z-ПФ):
| Алгоритм | Требуемое быстродействие | Объём памяти |
 а) с двумя буферами б) с одним буфером |
24(m+k+1) / Tц | 9m+9k+12 |
 |
52k / Tц | 20k+10 |
 |
50k / Tц | 19k+8 |
Дискретную ПФ можно представить в любой из форм:
 |
W(z
) = |
 |
Y(z) |   |
b0+b1z-1+...+bmz-m | - стандартная форма для дискретных ПФ |
 |
 |
|||||
| X(z) | a0+a1z-1+...+akz-k |
 |
W(z
) = |
 |
Y(z) |   |
K |  |
1+e2z-1 |   |
1+ekz-1 | - разложение z-ПФ на множители [1] |
 |
 |
 |
 |
|||||||
| X(z) | 1+d1z-1 | 1+d2z-1 | 1+dkz-1 |
 |
W(z
) = |
 |
Y(z) |   |
P1 |   |
P2 |   |
Pk | - разложение z-ПФ на элементарные дроби [1] |
 |
 |
 |
 |
|||||||
| X(z) | 1+d1z-1 | 1+d2z-1 | 1+dkz-1 |
где: ei - нули z-ПФ; di - полюса z-ПФ; a0 - не равно нулю; Pi
- коэффициенты разложения
Этим формам представления z-ПФ соответствуют структурные схемы изображенные на рис. 1.

Рис. 1
Разложения

делают параметры z-ПФ независимыми, позволяют контролировать ряд дополнительных фазовых координат: x1[n], x2[n], ..., xk-1[n]; или y1[n], y2[n], ..., yk[n]
- что удобно при отладке систем.
Последовательная структура

удобна при синтезе дискретной коррекции.
Параллельная структура
удобна для построения цифровых регуляторов.
Разложение z-ПФ на элементарные дроби
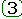
позволяет реализовать z-ПФ на параллельно работающих ЦВМ для повышения быстродействия.
Перечисленные факторы определяют выбор алгоритма программы для ЦВМ.
После разложений, каждый из множителей в форме

или каждую из элементарных дробей в форме
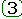
следует представить в стандартной форме

(с отрицательными степенями оператора z). Переход к разностным уравнениям будет един. z-ПФ в форме

соответствует разностное уравнение (РУ):

по которому и составляется программа. Поскольку текущее значение выходной координаты y[n] рассчитывается по предыдущим значениям y[n-1], y[n-2], y[n-k]
- данное РУ называется рекурсивным.
Изобразим структурную схему цифрового фильтра для этого уравнения (см.
рис. 2). Ее можно преобразовать, объединив два буфера (см. рис. 3). Цепочки элементов z-1 в программах будут соответствовать буферам из ячеек памяти, данные в которых сдвигаются на каждом такте дискретизации. Обе структурные схемы можно составить из простейших блоков программы VisSim.

Структурной схеме соответствует алгоритм

Условие физической реализуемости - а0 № 0
Рис. 2

Структурной схеме соответствует алгоритм

Условие физической реализуемости - а0 № 0
Рис. 3
Если выбран последовательный

или параллельный
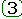
алгоритм, то структура каждого множителя или элементарной дроби первого порядка (см. рис. 1) будет иметь более простой вид (см. рис. 4).

Рис. 4
Согласно структурной схеме рис. 2, составим процедуру реализующую дискретную ПФ второго порядка:
function y_zW(x) { y=( k * (x*b0+xz_1*b1+xz_2*b2) - ( yz_1*a1+yz_2*a2) ) / a0; xz_2=xz_1; xz_1=x; yz_2=yz_1; yz_1=y; return y; };
где: xz_2, xz_1 и yz_2, yz_1 - ячейки двух буферов, т.е. регистры задержки - z -1.
Выберем коэффициенты z-ПФ для расчета переходной характеристики и построим ее:
| K= | |||||
| b0= | b1= | b2= | |||
| a0= | a1= | a2= |
Амплитудно-фазовая (частотная) характеристика или годограф Найквиста
Амплитудно-фазовая характеристика (годограф Найквиста)
Графическое отображение для всех частот спектра отношений выходного сигнала САР к входному, представленных в комплексной форме. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка.

От АФХ порождаются все другие частотные зависимости:
U(w) - четная (для замкнутых САР P(w));
V(w) - нечетная;
A(w) - четная (АЧХ);
j(w) - нечетная (ФЧХ);
ЛАЧХ& ЛФЧХ - используются наиболее часто.
Аналитический расчет квадратичных ИТ-оценок
Для аналитического расчета можно воспользоваться теоремой Парсеваля:

Если ошибка x(t) = yҐ - y(t), то ее изображение:

Для нахождения I и I' мы должны подавать сигналы 1(t) и 1'(t). Их изображения Фурье соответственно равны:

Тогда установившиеся значения выходной координаты и, соответственно, значения ПФ для этих режимов:
yҐ = 1,
F(0) = 1 и yҐ
= 0, F(0) = 0.
В итоге изображения ошибок:

А квадратичные ИТ-оценки:

Аппроксимация звена чистого запаздывания
Рабочие файлы: [Аппроксиматоры]


Поскольку они существенно похожи, в приближенных расчетах можно осуществлять подмены передаточных функций звеньев.


Если N®Ґ, то в пределе получим W(s)»e-ts. Уже при N=8..10 степень приближения высока. Ряд будет более точно соответствовать разложению в ряд функции e-ts, если его представлять не апериодическими, а фазосдвигающими звеньями.
Архитектура математического ядра моделирующих программ с поточной моделью управления
Какими бы разными ни были моделирующие программы, вариации архитектуры их математических ядер довольно жестко ограничены возможностями компиляторов языков высокого уровня. Очевидно, что математическое ядро должно поддерживать от 100 до нескольких тысяч математических функций. Безусловно, требуется формализация интерфейса настройки и управления математического ядра, поскольку справиться с таким громадным количеством функций, используя их ручной вызов, невозможно.
Возможности современных версий языка Си++ позволяют решить поставленную задачу следующим образом. Пишется полиморфный класс CBlkTemplate с виртуальным методом Calc (см. табл. 1). Его наследуют классы, составляющие библиотеку математических функций. В частности, каждый потомок реализует метод Calc в виде уникальной математической функции. Уточним возможности, которые предоставляет подобная организация библиотеки.
Во первых, от каждого математического класса можно породить любое количество объектов. Это означает, что для обработки повторно встречающихся в модели математических функций будут использованы уникальные экземпляры объектов, каждый из которых будет иметь собственную область памяти для хранения возвращаемых значений Output[k]. В результате не будет наблюдаться "затирание" координат модели.
Во вторых, в силу действующих стандартов для компиляторов языка Си++, объекты порожденные от разных потомков полиморфного класса (CBlkTemplate) будут иметь реализации виртуальной таблицы функций (vtbl) одной размерности. Это означает, что их можно присвоить элементам одного массива MathBlock[i] (см. рис. 3). Что, в свою очередь, открывает возможности для создания автоматизированных процедур обслуживания объектов математического ядра. Так например, процедура исполнения шага симуляции модели в таких программах, как VisSim, Simulink, MBTY может иметь следующий вид:
Листинг 1
for (i=0; i < numBlock; i++) { MathBlock[i]->Calc(); }
Подобных процедур не много, и, в случае реализации математического ядра в виде COM-сервера, они образуют его интерфейсы (см.
табл. 2).
Уделим внимание деталям реализации математического ядра. В табл. 1 приведён список важнейших атрибутов полиморфного класса, которые наследуются всеми его потомками. К ним относятся: массив указателей на аргументы pInput[j], массив возвращаемых функцией результатов Output[k] и массив параметров функции Param[n]. Размерность массивов задается значениями параметров конструкторов потомков, которые, в свою очередь, передаются им через интерфейс createBlock COM-сервера (см. табл. 2).
| Таблица 1 |
| Атрибуты полиморфного класса - общего предка всех математических классов |
| CBlkTemplate.pInput[j] |
| CBlkTemplate.Output[k] |
| CBlkTemplate.Param[n] |
| CBlkTemplate.Calc() = 0; // virtual |
| CBlkTemplate. ... |
делает возможным (в графическом представлении) их соединение линиями связи в требуемом порядке. Эта операция осуществляется через интерфейс createWire COM-сервера (см. табл. 2). Её результатом является присвоение значения указателя на элемент массива Output[k] одного объекта элементу массива pInput[j] другого объекта (см. цепочку повторяющихся фрагментов на рис. 3). Таким образом, совокупность показанных программных решений делает возможным создание моделей систем из любого требуемого набора математических функций, между которыми возможна любая требуемая схема передачи аргументов.

Рис. 3
В целях ознакомления с интерфейсами математического ядра (COM-сервера) рассмотрим программу на VB, которая создает модель динамической системы и запускает процесс симуляции в пакетном режиме (для расшифровки параметров методов см. табл. 2).
Листинг 2
' Объявляем переменную, как математическое ядро
Private WithEvents Mdl As SimKernel Private mySmplArr(100) As Double
' Создаём из COM-сервера объект - математическое ядро
Set Mdl = CreateObject("Klinachyov.SimKernel")
' Устанавливаем свойства симуляции модели
Mdl.setSimProp 0, 1, 0.01, 0
' Создаем блоки (математические объекты или функции)
Mdl.createBlock L702, 0, 1, 0 ' inpVector
Mdl.createBlock L101, 2, 1, 2 ' summingJunction
Mdl.createBlock L100, 1, 1, 1 ' gain
Mdl.createBlock L951, 1, 1, 1 ' 1/S
Mdl.createBlock L802, 1, 0, 0 ' outVector
Mdl.createBlock L800, 2, 0, 0 ' export
' Устанавливаем параметры блоков и начальные условия
Mdl.setBlkParam 2, 1, 1 Mdl.setBlkParam 2, 2, -1 Mdl.setBlkParam 3, 1, 4 Mdl.setBlkParam 4, 1, 0
' Создаем связи между блоками (схему передачи аргументов)
Mdl.createWire 1, 1, 1, 2 Mdl.createWire 2, 1, 1, 3 Mdl.createWire 3, 1, 1, 4 Mdl.createWire 4, 1, 2, 2 Mdl.createWire 2, 1, 1, 6 Mdl.createWire 4, 1, 2, 6 Mdl.createWire 4, 1, 1, 5
' Устанавливаем очередность исполнения блоков
Mdl.BildSimFlow
' Это не важно - задаем массив выборок для обработки моделью
For i = 0 To 99 mySmplArr(i) = Sin(i / 7) Next
' Передаем массив в математическое ядро
Mdl.swapInputOutputSamples mySmplArr
' Запускаем процесс симуляции модели
Mdl.Simulation
' Считываем обработанный моделью массив
Mdl.swapInputOutputSamples mySmplArr
' Запускаем сервер визуализации результатов
' ...
Беглого взгляда на программу достаточно, дабы сделать вывод о том, что процесс создания модели унифицирован (для создания любого математического блока или же любой межблочной связи используется только один соответствующий метод (интерфейс)). Именно жесткая унификация интерфейсов делает возможным создание шлюзов между редакторами векторной графики и математическими ядрами.
 Интерфейсы (методы) COM-сервера - математического ядра Интерфейсы (методы) COM-сервера - математического ядра |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Авторское предисловие к Договору
Даже в тяжёлые для России годы общественного переустройства фирма
Visual Solutions Inc уделяла не мало внимания российским пользователям своего программного продукта. На протяжении продолжительного времени в России действует уникальная схема распространения программы VisSim на бесплатной основе для академических пользователей. В немалой степени она способствовала обновлению учебного процесса в вузах России. Я был приятно удивлен, когда получил официальный запрос лично от президента фирмы Питера Дарнелла с просьбой о возможности включения данного моего произведения в дистрибутивный пакет программы VisSim для русскоговорящих пользователей, без нарушения выбранной для него стратегии распространения. Строго говоря, фирма имела право сделать это молча, но предпочла официально попросить. Именно по этим причинам я принял решение публично передать фирме Visual Solutions Inc
Почетное право распространять мое произведение.
Клиначёв Николай Васильевич
Безинерционный элемент (активноесопротивление)
Иконка безинерционного потребителя энергии, а так же его внутренняя структурная схема показаны на рисунке. От верхнего разъема к нижнему (зеленые контакты) по элементу протекает поток материи i. Потенциал
j2 на красном контакте нижнего разъема элемента известен (определяется другими элементами цепи). Потенциал j1
красного контакта верхнего разъема вычисляется с помощью закона Ома, поскольку величина потока i и сопротивление R для элемента известны:
j1 = j2 + i R.

Библиотеки блоков графических языков
В графических инструментальных средах информационные потоки определяются блоками, которые могут иметь входы и выходы. В библиотеках программ может присутствовать несколько сотен блоков. Блоки можно классифицировать:
Блоки - источники сигналов
Блоки - преобразователи сигналов
Блоки - приемники сигналов
Блоки, которые одновременно являются источниками, приемниками и преобразователями сигналов, т.е. это блоки обладающие эффектом памяти (кроме "УВХ")
Блоки (структуры) для программирования потока
Блоки (структуры) для синхронизации потоков
Большое количество блоков может наблюдаться только в группе преобразователей сигналов. Минимально необходимым является количество 100+/-10
блоков. Это блоки элементарных математических операций:
Арифметические
Логические
Трансцендентные
Матричные
Нелинейные
Обладающие эффектом памяти
Практически все языки графического программирования поддерживают инкапсуляцию смыслового фрагмента информационного потока, т.е. небольшого фрагмента блок-схемы, в одном составном блоке. Этот механизм является основой при составлении иерархически структурированных программ (моделей), а так же позволяет расширить библиотеку базовых блоков блоками пользователя, которые, в последствии, можно многократно использовать (например, типовые динамические звенья).
Билеты-задачи по ТАУ к государственному экзамену
Задача № 1 ТАУ
Выбрать оптимальный метод и повысить точность системы, если известна её частотная характеристика в разомкнутом состоянии (система имеет единичную обратную связь (ОС)).

Совокупность возможных методов повышения точности ограничена требованием сохранить линейность системы. Решение задачи должно быть выполнено (подтверждено моделированием) системы в пакете VisSim. Блок-схему (модель) системы составить и сдать комиссии до подхода к ЭВМ.
Задача № 2 ТАУ
Выбрать оптимальный метод, и выполнить коррекцию системы, модель которой изображена на рисунке.

Совокупность возможных методов коррекции ограничена требованием сохранить линейность системы. Решение задачи должно быть выполнено (подтверждено моделированием) системы в пакете VisSim. Асимптотические ЛАЧХ & ЛФЧХ построить и сдать комиссии, указав название метода коррекции, до подхода к ЭВМ.
Задача № 3 ТАУ
Указать настройки ПИД-регулятора, формирующего управляющее воздействие на объект, передаточная функция которого изображена на рисунке (система имеет единичную ОС). Требования к точности системы: Vm=10ед./с; Em=100ед./с2; Xm=0,01ед. Требование к устойчивости: M < 1,16.

Решение задачи должно быть выполнено (подтверждено моделированием) системы в пакете VisSim. Фрагменты ЛАЧХ & ЛФЧХ, удовлетворяющие предъявленным к системе требованиям построить и сдать комиссии до подхода к ЭВМ.
Задача № 4 ТАУ


Решение задачи должно быть выполнено (подтверждено моделированием) системы в пакете VisSim. ЛАЧХ & ЛФЧХ разомкнутой, некорректированной системы, а так же ее блок-схему построить и сдать комиссии до подхода к ЭВМ.
Задача № 5 ТАУ
Определить запасы устойчивости по амплитуде и фазе для системы изображенной на рисунке. Найти выражение для ошибки системы x(t) в установившемся режиме работы при заданном входном сигнале.

Решение задачи должно быть выполнено (подтверждено моделированием) системы в пакете VisSim. До подхода к ЭВМ предъявить комиссии асимптотические ЛАЧХ & ЛФЧХ разомкнутой системы, выражение для сигнала задания g(t) и значения первых трех коэффициентов ошибок замкнутой системы.
Билинейное преобразование
Рабочие файлы: [Аппроксиматоры]
Билинейное преобразование
Бинаправленная процедура пересчета коэффициентов линейной модели, используемая с целью нахождения соответствующего (дискретного или непрерывного) аналога, т.е. для трансформации моделей из s-домена в z-домен и обратно.
В действительности, при выполнении процедуры билинейного преобразования моделирующие программы никакого "символьного анализа" не выполняют (название отражает лишь суть результата). Для пересчета коэффициентов модели используются чуть модифицированная, а, по сути, та же процедура идентификации коэффициентов, которая была описана выше.
Если требуется перейти от непрерывного прототипа к дискретной модели, то процедура идентификации (в данном случае "перерассчитываемых") коэффициентов будет отличаться лишь тем, что библиотека анализа подключится не к выводам интеграторов модели, а к регистрам задержки, на которых эти (квазианалоговые) интеграторы реализованы. Следует уточнить, что в этой процедуре имеет смысл использовать лишь квазианалоговый интегратор первого порядка (на одном регистре), реализующий метод трапеций, поэтому библиотеки автоматически активируют этот метод интегрирования в настройках программ.
Если же требуется обратная трансформация модели, то процедура идентификации "перерассчитываемых" коэффициентов так же чуть модифицируется. Библиотека анализа замещает все регистры задержки модели их непрерывными аналогами – фазосдвигающими звеньями и подключается к интеграторам, на которых эти аппроксиматоры реализованы.

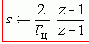
Если каждую из формул чуть преобразовать и вспомнить известную формулу, связывающую передаточные функции замкнутой и разомкнутой системы, то легко можно составить структурные схемы, используемые библиотекой в процедуре трансформации моделей (см. рис.), а так же увидеть в них передаточные функции: регистра задержки, фазосдвигающего звена; интегратора, и квазианалогового интегратора реализующего метод трапеций:
Блоки обладающие эффектом памяти
Фундаментальными для построения моделей являются блоки обладающие эффектом памяти. В этой группе два элементарных блока:
1/S
– "Интегратор" (дискретный квазианалог интегратора)
1/Z – "Регистр задержки"
Интеграторы используются для построения моделей, которые имеют непрерывную природу, регистры задержки составляют основу моделей с дискретной природой.
В библиотеках программ математического моделирования можно найти еще ряд блоков обладающих эффектом памяти:
Блок "Передаточная функция"
Блок "Пространство состояний"
Блок "Звено чистого запаздывания"
Блок "Устройство выборки-хранения"1
Эффект памяти необходим так же при создании некоторых нелинейных блоков, таких как компаратор с гистерезисом. Но, обычно, подобные блоки в базовую библиотеку специально не включаются.
Эффект памяти проявляется двояко. Если речь идет, об интеграторах, то, очевидно, что их выходное значение зависит не только от текущего входного значения, но и от всей истории входных значений:
y[n]= y[-1] + m=0n-1е
x[m] ,
где: x[n] - входной сигнал, y[n] - выходной сигнал, n - индекс решетчатой функции.
В регистрах задержки эффект памяти проявляется в том, что выборки сигнала задерживаются (а для этого запоминаются) на одну дискрету времени, период которой определяет внешняя синхронизирующая последовательность (внешний синхросигнал). Математическая запись соответствующей операции имеет вид:
y [n] = y [n-1] .
1) Следует помнить, что УВХ является лишь преобразователем сигнала, т.е. не порождает информационный поток.
Частотная передаточная функция
Рабочие файлы: [Измерение ЧХ]
Если на вход любой системы подать сигнал синусоидальной формы:
x(t) = Xm cos(wt) = Xm e jwt .
Очевидно, что выходной сигнал будет иметь ту же форму:
y(t) = Ym cos(wt+j) = Ym e j(wt+j) .
Зависимость же между амплитудами и фазами выходного и входного сигналов определяет ДУ движения системы. Возмем произвольное, считая помеху f(t) равной нулю:
(T22 p2 + T1
p + 1) y(t) = (k1 + k2
p) x(t) .
Подставим сигналы в уравнение движения:
T22(jw)2
Ym e j(wt+j) + T1(jw) Ym e
j(wt+j) + Ym e j(wt+j) = k1 Xm e jwt + k2(jw) Xm e
jwt .
Найдем отношение выходного сигнала ко входному:

Заметим. Если вместо подстановки сигналов записать ДУ движения системы для домена Лапласа и вновь найти отношение выходного сигнала к входному (а точнее их изображений), то полученная в ходе этого преобразования ПФ совпадет с точностью до свободной переменной с частотной ПФ.
Резюме1: Частотная передаточная функция получается из обычной заменой оператора Лапласа s на комплексную частоту jw, т.е. в результате перехода от изображения Лапласа к изображению Фурье.
Резюме 2: ДУ движения системы связывает входной и выходной сигналы (т.е. функции времени), ПФ связывет изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры.
Частотные характеристики
Частотная передаточная функция может быть представлена в следующих видах:
W(jw) = A(w) e jj(w), или W(jw) = U(w) + jV(w) ;
где:
A(w) - модуль частотной передаточной функции - находится как отношение модулей числителя и знаменателя:
A(w) = (k12 + k22
w2)1/2 / ((1 - T22
w2)2 + T12
w2)1/2 .
j(w) - фаза частотной передаточной функции - находится как разность аргументов числителя и знаменателя:
j(w) = arctg(k2w / k1) - arctg(T1w / (1-T2w2)).
U(w) и V(w) - вещественная и мнимая части частотной ПФ. Для их нахождения немобходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину.
Частотные критерии качества
Частотные критерии качества применяют, когда известны или можно определить экспериментально частотные свойства САР (АФХ, АЧХ, ЛАЧХ& ЛФЧХ). Вид переходного процесса при этом не рассматривается.
Оценить частотными критериями можно:
Запас устойчивости (b; m1; M)
Быстродействие САР (wр; wср; wп; wэк).
Частотные свойства последовательных
Рабочие файлы: [zvenya_kor.vsm]
К основным корректирующим звеньям относятся:
Пассивное интегрирующее звено
Пассивное дифференцирующее звено
Пассивное интегро-дифференцирующее звено
Фазосдвигающее звено
Антивибратор






где: T1 = (R1+R2)C2; T2
= R2C2; T3 = R1C1; T4 = (R1||R2)C1.





Отмеченный участок ЛАЧХ корректирующих звеньев 1, 2 и 3, должен так изменить вид корректируемой ЛАЧХ, чтобы она в том же диапазоне частот пересекала ось частот с наклоном -20 дБ/дек.
Частотные свойства систем с запаздыванием. Понятие о критическом запаздывании
Перейдем в частотный домен:

следовательно:
L(w) = |W(jw)| = Ao(w) ґ 1 = Ao(w) ,
j(w) = jo(w) - wt
.

Таким образом, наличие звена с запаздыванием не меняет модуля, а лишь вносит дополнительный фазовый сдвиг (-wt).
Из графика видно, что звено e-ts
закручивает исходный годограф Wo(jw) по часовой стрелке, ухудшая условия устойчивости.
По имеющемуся годографу Wo(jw) можно определить критическое значение запаздывания tкр:
| j1 -
wсрtкр = -p |
=> | tкр
= (p + j1) / wср |
В некоторых случаях tкр можно рассчитать аналитически.
Частотный анализ моделей и систем
Частотный анализ модели или системы
Процесс идентификации частотной характеристики модели или системы сопровождаемый уточнением соответствующей частотной передаточной функции. Цель частотного анализа состоит в предоставлении исходных данных для решения задач оценки качества, коррекции, синтеза САР.
Процедуры частотного анализа, реализованные в программах математического моделирования динамических систем, могут быть основаны на базе:
вычислительных алгоритмов;
измерительных алгоритмов;
алгоритмов распознавания образов.
Численные методы решения нелинейных
Решить систему уравнений [f(xn)] = 0 численно — значит найти, а точнее подобрать (подогнать) такие значения [xn], которые обнулят систему полиномов [f(xn)]. В процессе подгонки, по текущим результатам нужно принимать решение о том, какие значения искомых переменных [xn+1] подставлять в следующий раз (n – индекс текущего приближения корня). Для этого существуют разные методы.
Метод Ньютона для решения уравнения и системы уравнений:
xn+1 = xn - f(xn) / f '(xn) ,
[xn+1] = [xn] - [f '(xn)]-1
[f(xn)] .
Метод Ньютона-Рафсона предполагает возможность относительного изменения шага итерации a:
[xn+1] = [xn] - [f '(xn)]-1
[f(xn)] an .
Модифицированный метод Ньютона предполагает замораживание инверсной матрицы производных (инверсного Якобиана) на первом шаге:
[xn+1] = [xn] - [f '(x0)]-1
[f(xn)] .
Но в этом случае наблюдается лишь линейное схождение. Хотя, через несколько итераций, инверсный Якобиан можно обновлять.
Метод секущих:
xn+1 = xn - f(xn) (xn - xn-1) / (f(xn) - f(xn-1)) .
Здесь невозможно вести речь об оценке производной конечной разностью, поскольку шаг итерации очень большой.
В VisSim'е, переменной xn соответствует блок "неизвестная", а блок "нулевой баланс" считывает с модели значение функции f(xn). Приведенные же выше формулы используются для расчета значения на выходе блока "неизвестная" на следующем шаге итерации.
Основные итерационные методы сходятся весьма быстро. Для того чтобы текущее приближение стало более чем в миллион раз ближе к корню, методу дихотомии
требуется 40 итераций, методу золотого сечения – 29, методу Ньютона еще меньше. Очевидно, что линейные системы уравнений решаются за одну итерацию. А ими, например, описываются почти все задачи дисциплины "ТОЭ" изучаемые студентами в вузе.
Что же с ТОЭ? или О структурном
На первый взгляд признаки кризиса в методике преподавания блока дисциплин связанных с расчетом цепей преобразования энергий, который, как предполагает автор этих строк, проявится к 2015..2020 годам, практически не видны. Более того, каждая из тех 7..9 дисциплин, на которые кризис повлияет, имеет не просто хорошие учебники, а самые лучшие, поскольку их содержимое шлифовалось талантливыми педагогами страны без изменений сути излагаемых вопросов уже более 30..50 лет. Для примера сравните учебники по ТОЭ, электроприводу, гидропневмоавтоматике и т.д., с переводной литературой, которую педагоги вынуждены использовать в качестве учебной по современным технологиям программирования.
Какова же причина грядущего кризиса, если сегодня у названных дисциплин имеется блестящее методическое обеспечение, наработанное на основе совокупности фундаментальных законов, в ряду которых не прогнозируются подвижки? Ответ прост – это появление нового вычислительного инструментария – программ мультидоменного математического моделирования динамических систем. Попробуем обосновать данное утверждение.
Цифровая коррекция
Цифровая или дискретная коррекция весьма интересна с практической точки зрения в силу конструктивной универсальности устройств и гибкости настройки. Решения задач коррекции предполагают модификации низкочастотного и среднечастотного фрагментов ЛАЧХ, как правило, с уменьшением частоты среза
wср. Известно, что в этом диапазоне системы с ЦВМ и их ЛАЧХ - L(l) не отличаются существенно по свойствам от непрерывных аналогов. Поэтому методика синтеза коррекции едина для цифровых и непрерывных систем. Проектирование же дискретной коррекции ведется в четыре этапа.
Синтез ПФ непрерывного корректирующего устройства Wк(s)
по методикам разработанным для непрерывных систем.
Переход от непрерывной ПФ корректирующего устройства Wк(s)
к эквивалентной дискретной Wк(z)
посредствам последовательных переходов по изображениям:

с помощью результирующей формулы билинейного преобразования (т.е. формальной подстановки):
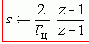
где: Tц - период дискретизации ЦВМ.
Составление структурной схемы дискретной ПФ Wк(z), оптимизированной при реализации по объёму памяти, быстродействию или для контроля промежуточных фазовых координат системы.
Написание программы для ЦВМ (периферийный контроллер, микроЭВМ, ЭВМ, цифровой сигнальный процессор - DSP) или разработка схемы на цифровых микросхемах.
Заметим, что из непрерывной ПФ можно получить бесконечное количество вариантов дискретной ПФ, при разных периодах дискретизации ЦВМ (этап 2).
Обычно частоту дискретизации fц=1/Tц выбирают в 6..10 раз больше частоты среза fср разомкнутой системы. Первоначально частоту дискретизации выбирают большой (fц=10..30fср), за тем, за две три попытки стремятся ее уменьшить (т.е. повторяют этап 2). При низких частотах дискретизации качество переходного процесса ухудшается настолько (в сравнении с непрерывной коррекцией), что платить за это понижением производительности ЦВМ не представляется возможным. Соответствующую ПФ
Wк(z) используют в дальнейшем.
При синтезе ПФ Wк(s) или Wк(z) необходимо, что бы степень числителя Wк(s)
не была больше степени знаменателя или свободный коэффициент a0
в знаменателе ПФ Wк(z)
не был нулевым, иначе невозможно реализовать программу.
Если требуется обратный переход от Wк(z)НЧ
к Wк(s)НЧ следует воспользоваться обратной формулой билинейного преобразования:

Этот переход однозначен при известном периоде работы ЦВМ Tц.
Цифровые регуляторы
В непрерывных системах широко используются PID-регуляторы, которые представляются идеализированным уравнением:

где: KP - коэффициент усиления пропорционального канала; TIx - постоянная времени сопрягающего полюса интегрального канала; TDx - постоянная времени сопрягающего полюса дифференциального канала.
Для малых периодов дискретизации Tц уравнение может быть преобразовано в разностное без существенной потери в точности. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников




В результате получен нерекуррентный (позиционный) алгоритм управления, который требует сохранения всех предыдущих значений сигнала ошибки
x[i], и в котором каждый раз заново вычисляется управляющий сигнал u[n].
Для реализации программ закона регулирования на ЦВМ более удобным является рекуррентный алгоритм. Он характеризуется тем, что для вычисления текущего значения сигнала u[n] используется его предыдущее значение u[n-1] и поправочный коэффициент, не требующий существенных вычислительных затрат. Определим его:

Перенесем u[n-1] в правую часть - получим "скоростной" алгоритм для программной реализации регулятора:
(*)
u[n] = u[n-1] + b0
x[n] + b1 x[n-1] + b2
x[n-2].


Преобразования, аналогичные выше изложенным, при получении рекуррентного соотношения (*), выявляют отличия только для коэффициента b0:

Запишем РУ (*) для изображений в z-домене:
U [z] (1- z -1) = (b0
+ b1 z -1 + b2 z
-1) X [z] ,
и представим его в виде дискретной ПФ:

Анализ ее коэффициентов показывает, что:
Для исключения статической ошибки, ПФ должна иметь полюс zx=1.
Если b2 = 0, то получим PI-регулятор.
Если b0 = 0, а b1 = (1 + b2), то получим PD-регулятор.
Цифровые системы
Цифровые системы строятся на базе комплекса средств вычислительной техники, основными элементами которого являются: 1)ЦВМ, 2) устройства ввода, 3) устройства вывода.
Функции ЦВМ могут выполнять: 1) ЭВМ (компьютеры), 2) DSP - цифровые сигнальные процессоры, 3) ЦУ на жесткой логике. Первые относятся к универсальным устройствам управления, вторые специализированны для приложений, третьи разрабатываются для конкретных устройств (например, цифровой фильтр, имеющийся в каждом еD АЦП).
Устройствами ввода и вывода в случае состыковки с аналоговыми сигналами являются АЦП и ЦАП-ы, а в случае состыковки с цифровыми сигналами - порты и интерфейсы.
В системах с ЦВМ, последние могут выполнять роли: 1) регулятора, 2) регулятора и устройства сравнения, 3) корректирующего устройства или 4) самого объекта.
Если ЦВМ универсальная (ЭВМ), то возможно построение многофункциональных САУ, когда одна ЦВМ обслуживает комплекс составляющих объект устройств. Например, в автомобиле: 1) система навигации, 2) система бортового электропитания, 3) АБС, 4) электронная подвеска, 5) управление топливоподачей, ... В подобных случаях в состав системы ЦУ должны входить аналоговые или цифровые мультиплексоры и демультиплексоры.
Во всех случаях ЦВМ предоставляет легко доступные информационные потоки, позволяющие кроме прямого управления осуществлять функции: 1) контроля, 2) оптимизации, 3) координации и 4) организации всех процессов.
Кликая мышкой по столбцу цветовой
| Резистор: | 000e+0 Ом; 5%, ряд E24 (золотое кольцо) |
| 0 черный | Кликая мышкой по столбцу цветовой палитры можно "заполнить цветами кольца резистора". Процедура заполнения цветовых колец зациклена, и возможно повторение процедуры дешифровки номинала. Если кликнуть по кольцу кода точности резистора, то добавится третье "кольцо номинала" для прецизионных резисторов. Следует помнить, что "кольцо точности" может быть и других цветов, а так же то, что встречаются резисторы с кольцом "ТКС" (самое последнее; не показано). | |
| 1 коричневый | ||
| 2 красный | ||
| 3 оранжевый | ||
| 4 желтый | ||
| 5 зеленый | ||
| 6 синий | ||
| 7 фиолетовый | ||
| 8 серый | ||
| 9 белый | ||
| -1 золотой | ||
| -2 серебряный |
for (i=0; i
Мантиссы E24: 10,11,12,13,15,16,18,20,22,24,27,30,33,36,39,43,47,51,56,62,68,75,82,91
Демпфирование с подавлением низких частот или эквивалентным поднятием высоких
Применяется ограниченно, поскольку без восстановления коэффициента усиления в области низких частот, падает точность, а поднятие верхних частот расширяет полосу пропускания и увеличивает шумы в системе.
Реализуется с помощью пассивного дифференцирующего звена, которое не дает дополнительных отрицательных фазовых сдвигов в области низких частот и позволяет успешно корректировать ЛАЧХ с наклоном -40 дБ/дек. Компенсировать же падение коэффициента усиления DK = T3 / T4
можно, если только наклон -40 дБ/дек после частоты среза wср
сохраняется более одной декады.


Демпфирование с подавлением средних частот
| Применяется наиболее часто, поскольку позволяет сохранить точность САР и полосу пропускания (быстродействие). Реализуется с помощью пассивного интегро- дифференцирующего звена. Позволяет успешно корректировать ЛАЧХ с наклоном -40 дБ/дек. Однако корректирующее звено вносит дополнительные отрицательные фазовые сдвиги в НЧ области. |
 |
Демпфирование с подавлением высоких частот
Применяется сдержанно, поскольку при сохранении точности существенны потери в быстродействии - режется полоса пропускания.
Реализуется:
C помощью апериодического звена с большой постоянной времени T0
- только для точных статических систем T0і K T1
(подобный тип коррекции в ОУ).
C помощью пассивного интегрирующего звена - для систем имеющих участок ЛАЧХ с наклоном -20 дБ/дек вблизи частоты единичного усиления (среза)
wср, на которой наклон может составлять -40, -60, .. дБ/дек.


Дифференцирование и интегрирование решетчатых функций
Рабочие файлы: [S & 1/S]


D f [n] = f
[n+1] - f [n],
либо первая обратная разность:
С f [n] = f
[n] - f [n-1].
Аналогами второй производной являются вторые разности. Прямая:
D2 f [n] = D f
[n+1] - D f [n]
= (f [n+2] - f [n+1]) - (f
[n+1] - f [n]) = f [n+2] - 2 f
[n+1] + f [n],
и обратная:
С2 f [n] = С f
[n] - С f [n-1] = f
[n] - 2 f [n-1] + f
[n-2].
По аналогии могут определяться и высшие разности:
| Dk f
[n] = n=0kе(-1)nCknf [n+k-n] |
Сk f
[n] = n=0kе(-1)nCknf [n-n] |
где: Ckn = k! / (n!(k-n)!).
Очевидно, что если f [n] определена только для положительных n, то для n=0 все обратные разности
Сk f [n] равны нулю, что позволяет ...

s[n] = m=0n-1е
f [m] = n=1nе
f [n-n],
и полная сумма:
so[n] = s[n] + f
[n].
Дискретная ПФ
Знание приведенной решетчатой весовой функции wп[n] позволяет найти реакцию импульсного фильтра на входную величину произвольного вида - x(t). Рассмотрим реакции на отдельные значения входной величины в дискретные моменты времени:
на x[0]: y[n] = wп[n] x[0]
на x[1]: y[n] = wп[n-1] x[1]
на x[m]: y[n] = wп[n-m] x[m]
Следовательно реакция на всю входную последовательность будет равна:
y[n] = m=0nеwп[n-m] x[m] = m=0nеwп[m] x[n-m] = m=0nеwп[m] x[n] e -mTs = m=0nеwп[m] x[n] z -m = x[n] m=0nеwп[m] z -m .
Здесь первоначально изменен порядок суммирования (свертка), а затем учли запаздывание оператором запаздывания z = eTs. Если устремить n к бесконечности, то, очевидно, что сомножитель для x[n] есть дискретная ПФ:
W (z) = n=0Ґ еwп[n] z -n = Y (z) / X
(z) .
И поскольку она является Z-преобразованием приведенной решетчатой весовой функции, то ее можно представить как Z-преобразование от обратного преобразования Лапласа приведенной ПФ экстраполятора и непрерывной части:
W (z) = Z { wп[n] } = Z { L-1 {
Wп(s) } } .
Часто для краткости записи знак операции L-1 опускают записывая: W (z) = Z { Wп(s) }.
Дискретная синусоидальная последовательность
Рабочие файлы: [aliasing.vsm][z_sin2.vsm]
[psd45.vsm] [fft30.vsm] [Свойства W(e jwT)]

Особые свойства последовательности x[n]:
Функция может быть как периодической - рис. а и б, так и непериодической - рис. в.
Амплитуда образующей непрерывной функции может быть максимальным значением последовательности x[n] - рис. а, и может не является им - рис. б.
Последовательность не изменится, если на вход ключа подавать сигналы с частотами, отличающимися на частоту дискретизации: f ; f + 1f0;
f + 2f0; ...; f + kf0.
Запишем закон изменения синусоидальной последовательности в экспоненциальной форме:
x[n] = a sin [wnT+j] = a e
j[wnT+j] = a e
jj e jwnT = a e
jwnT = a zn
,
тогда выходная величина импульсного фильтра:
y[n] = m=0Ґ еwп[n-m] x[m] = m=0Ґ еwп[m] x[n-m] = m=0Ґ еwп[m] a zn-m = a zn
m=0Ґ еwп[m] z -m = a znW (z) = x[n] W (z).
Таким образом ПФ W(z) при подстановке z = e jwT - есть частотная ПФ. Все остается в силе и для F(e
jwT) и
Fx(e jwT).
Очевидно, что частотные ПФ W(e jwT), F(e jwT)
и Fx(e jwT)
обладают периодическими свойствами (w0 = 2pT -1). Это видно и из нижнего рис., поскольку одну и ту же входную последовательность могут вызывать входные сигналы с разными частотами f + k f0.
Договор передачи Почетного права распространения авторского произведения
22 января 2004 года Клиначёв Николай Васильевич (далее Автор), с одной стороны, и фирма Visual Solutions Inc в лице президента фирмы Питера Дарнелла (Peter Darnell), с другой стороны, заключили договор о нижеследующем:
Другие связывающие отношения
Разделим уравнение движения (4) на уравнение ошибки (5), считая, что f(t)=0 и Wос(p)=1:
y(t) / x(t) = R(p) / Q(p) , => W(p) = R(p) / Q(p) .
В соответствии с теми же уравнениями и уравнением замыкания характеристический полином D(p) = R(p) + Q(p). Добавим 1 к W(p):
1 + W(p) = Q(p) / Q(p) + R(p) / Q(p) = D(p) / Q(p) .
При исследованиях характеристический полином приравнивают к нулю, т.е. вместо него можно использовать W(p):
1 + W(p) = 0 , - характеристическое уравнение.
А так же:
W(p) = [D(p) - Q(p)] / Q(p) = D(p)/Q(p) - 1 = R(p) / [D(p) - R(p)] .
и
W(p) = F(p) / [1 - F(p)] , W(p) = [1 - Fx(p)] / Fx(p) .
ДУ решенное относительно ошибки x(t) - уравнение ошибки
Рабочие файлы: [САР]
Если система ДУ (1) решается относительно ошибки системы, то получается уравнение ошибки замкнутой системы:
(5)
D(p) x(t) = Q(p)
g(t) + N(p) f(t)
где:
D(p)= a0pn + a1pn-1 + ... + an-1p + an
- характеристический полином;
Q(p) = D(p) - R(p) = c0pn + c1pn-1 + ... + cn-1p + cn
- коэффициенты полинома определяют влияние задающего воздействия g(t) на ошибку x(t);
N(p) = d0pk + d1pk-1 + ... + dk-1p + dk
- коэффициенты полинома определяют влияние помехи f(t) на систему.
ДУ решенное относительно регулируемой величины y(t) - уравнение движения
Рабочие файлы: [САР]
Система ДУ (1) может быть преобразована к одному уравнению путем исключения промежуточных координат (обычно выходную координату выражают через координату задания):

Результатом подобного преобразования является уравнение движения системы:
(4)
D(p) y(t) = R(p)
g(t) - N(p) f(t) ,
где:
D(p) = a0pn + a1pn-1 + ... + an-1p + an
- характеристический полином;
R(p) = D(p) - Q(p) = b0pm + b1pm-1 + ... + bm-1p + bm
- коэффициенты этого полинома определяют влияние задающего воздействия g(t) на регулируемую координату у(t), причем его степень меньше степени характеристического полинома, т.е. m<n;
N(p) = d0pk + d1pk-1 + ... + dk-1p + dk
- коэффициенты полинома определяют влияние помехи f(t) на систему.
Два подхода к получению исходных дифференциальных уравнений систем. Истинные и ложные модели
Рабочие файлы: [] [Принцип измерения ЧХ]
Если поставлена задача составления исходных ДУ САР, то возможны две ситуации. Либо детальная декомпозиция системы на модули и отдельные звенья возможна, либо нет.
Если декомпозиция возможна, то, опираясь на постулаты о сохранении материи и энергии (для соответствующего энергетического домена) и на закон Ома (в соответствующей формулировке), приступают к составлению исходных ДУ САР, т.е. к созданию истинной модели системы. Истинной будем называть такую модель или такое математическое описание, о которых известно, что они детально соответствуют физической природе системы.
Если декомпозиция на модули и звенья для системы невозможна, то, не имея детальной информации о ее физической природе, можно получить лишь ложную модель или ложное математическое описание, которые, однако, позволят исследовать систему и получить адекватные результаты. В этом случае совокупность исходных ДУ САР получают через частотный домен, путем экспериментального снятия частотных характеристик.
Для физической системы порядок системы ДУ ее истинной модели обычно в десять и более раз выше порядка системы ДУ ее ложной модели (например, для моделей ОУ). Тем обусловлена широкая популярность ложных моделей, и типовых звеньев, как структурных элементов для их создания.
Единичная функция. Дельта-функция. Типовые реакции систем
Рабочие файлы: [Интеграл Дюамеля] [Интеграл свертки]
[h(t) & w(t)] [Интеграл свертки]

Математическая функция, заданная условиями: 1(t)= 0
при t < 0, и 1(t) = 1 при
t > 0. Для автоматических систем является распространенным видом входного воздействия. Как правило, подобные воздействия сопровождают процессы включения систем и вызывают переходы от одного установившегося состояния к другому.

d(t)
Математическая функция, заданная условиями: d(t) ® Ґ
при t = 0, и d(t) = 0
при t № 0, - т.е. это импульс с бесконечной амплитудой, площадь которого принимается равной 1. Для автоматических систем является менее распространенным видом входного воздействия, чем единичная ступенчатая функция. Однако для теоретического описания последних имеет существенное значение. Подобные воздействия характерны для радарных комплексов, описывают передачу импульса при упругом взаимодействии и т.д.
Из определений функций 1(t) и d(t) очевидна связь между ними:
(1)
1(t) = т d(t) dt и d(t) = 1'(t).
Единичная ступенчатая функция 1(t) легка для практической реализации с высокой точностью, однако дельта-функцию Дирака d(t)
реализовать сложнее. Для теоретического описания систем и их моделирования ее можно грубо представить с помощью двух ступенчатых функций:
(2)
d(t) »
N 1(t) - N 1(t-e),
где: N - амплитуда функций, e - время, на которое запаздывает вторая ступенчатая функция, при этом N
e = 1 и e ® 0.
Переходный процесс на выходе типового звена или линейной системы, возникающий при подаче на вход единичной ступенчатой функции 1(t).

Переходный процесс на выходе типового звена или линейной системы, возникающий при подаче на вход короткого импульса, который, в приближении, можно рассматривать как дельта-функцию Дирака d(t).
В виду независимости присущих линейным системам свойств от внешних воздействий и наличия связи (1) между последними, подобное же отношение существует и для соответствующих типовых реакций:
h(t) = т w(t) dt и w(t) = h'(t).
Докажем эту взаимосвязь подав на систему грубую реализацию дельта-функции (2). В этом случае переходный процесс на выходе можно представить следующей суперпозицией:
y(t) = N h(t) - N
h(t-e),
которая будет являться функцией веса, предел которой (при
e ® 0) будет равен производной от переходной функции:
w(t) = lime®0( e N (h(t) - h(t-e)) / e ) = h'(t), - напомним: N
e = 1.
Функция веса связана с передаточной функцией преобразованием Лапласа:
W(s) = oҐ т w(t) e -st dt.
Переходная функция связана с передаточной функцией преобразованием Карсона:
W(s) = s oҐ т h(t) e -st dt.
Для произвольного входного воздействия, переходный процесс на выходе линейной системы может быть определен на основании интеграла Дюамеля-Карсона, если известны типовые реакции:
h(t): y(t) = x(0) h(t) + ot т x'(t) h(t-t) dt;
w(t): y(t) = ot т
x(t) w(t-t) dt, - так же "Интеграл свертки";
где: t - вспомогательное время интегрирования.
Форма Коши
Форма Коши
Матричная форма записи системы ДУ решенных исключительно относительно первой производной координат САР.

Изображенная на рисунке блок-схема позволяет решить систему ДУ представленную в форме Коши:
(2)

где:
x1, x2, x3 - собственные координаты системы - ошибка системы x(t), воздействие на объект u(t), выходная координата - y(t), ...;
a11, ... , a33 - постоянные коэффициенты (если система не является зависимой от параметра) - суммы и произведения постоянных времени Tj, коэффициентов усиления Kn;
f1, f2, f3 - воздействия на систему - сигнал задания g(t), помехи fj(t).
О форме Коши:
Применяется в теории управления не часто.
Удобна, если для расчетов использовать классические математические пакеты: MathCAD, MATLAB, Mathematica, Maple, Derive.
Используется при построении аналоговых вычислительных моделей матричного типа (например, моделей на операционных усилителях).
Уравнения могут быть решены относительно любой из фазовых координат xi.
Формирование запретной НЧ области для желаемой ЛАЧХ
Способ №1
Дано:
Xm - максимальная амплитуда ошибки;
Vm - максимальная скорость слежения;
Em - максимальное ускорение слежения.
Найдем связывающие отношения между амплитудой, скоростью и ускорением синусоидального сигнала:
| g(t) = Gmsin(wkt) g'(t) = Gmwkcos(wkt) g''(t) = -Gmwk2sin(wkt) |
=> | Vm = Gmwk Em = Gmwk2 |
=> | wk = Em / Vm Gm = Vm2 / Em |
Если зафиксировать Vm в сигнале и уменьшать
w от wk, то Gm
будет увеличиваться на 20 дБ за декаду (в 10 раз).
Если зафиксировать Em в сигнале и увеличивать
w от wk, то Gm
будет уменьшаться на 40 дБ за декаду (в 100 раз).



Способ №2
Дано:
wk - контрольная частота;
Dj - фазовая ошибка слежения;
d - относительная амплитудная составляющая ошибки.

- определяет вид запретной области (Kv и T1
- неизвестны).
Построим векторную диаграмму гармонических координат системы:

где:


Глоссарий терминов
Графов теория
Учение об общих топологических свойствах графов и о вытекающих из них расчетных методах. Две ветви теории: тероия направленных графов
и тероия ненаправленных графов четко делят между собой программы визуального математического моделирования.
Граф направленный, сигнальный
Диаграмма прохождения сигнала, состоящая из совокупности узлов (сумматоров) и соединяющих их ветвей. Стрелки на ветвях указывают направление передачи сигнала или воздействия от одного узла к другому. Ветви в направленном графе характеризуются передаточными функциями. Направленный граф является графической формой записи системы уравнений описывающих динамическую систему, и не может отражать ее топологию (модульную структуру).
Узел направленного графа
Сумматор координат модели динамической системы с одним выходом (поэтому узел направленного графа называют координатой). Обычно в каждом энергетическом домене в качестве координат выступают парные физические величины, чье произведение есть мощность. В пакетах математического моделирования эти парные физические величины называются координатами первого и второго рода. Выходные координаты ветвей собираются в узлы направленного графа согласно первому и второму законам Кирхгофа1. Узлы направленного графа, ровно, как и сам граф, не отражают различий в физической природе координат первого и второго рода (это непреодолимый недостаток направленных графов).
Ветвь направленного графа
Графический образ закона преобразования сигнала, который называется передаточной функцией. Если направленный граф есть истинная модель динамической системы и узлы графа отражают все ее координаты (граф не приведен), то передаточные функции ветвей есть либо закон Ома2, сформулированный для соответствующего энергетического домена и связывающий его физические величины первого и второго рода, либо другие физические законы, связывающие физические величины первого и второго рода разных энергетических доменов.
Граф ненаправленный, топологический (схема замещения)
Схема, состоящая из совокупности соединенных в узловых точках двухполюсных модулей преобразующих энергию. Полюсы двухполюсников являются подводами энергии. Для ветвей ненаправленного графа нельзя однозначно указать направление распространения координаты первого рода. Ненаправленный граф зеркально (без искажений) отражает модульную структуру (схему замещения) динамической системы
(энергетической цепи), и в том же графическом образе, но как в нелинейном зеркале, отражается ее система уравнений. Для узлов ненаправленного графа формулируются постулат о сохранении материи, а для контуров – постулат о сохранении энергетических потенциалов.
Узел ненаправленного графа
Условное графическое обозначение места соединения трех ветвей, в котором происходит либо распределение, либо аккумуляция координаты первого рода (потока материи). В любом ненаправленном графе узлов-распределителей и узлов-аккумуляторов материи равное количество. Различие математических моделей этих узлов, в силу единообразия физических конструкций, ни как не отражается в графическом представлении (т.е. в ненаправленном графе). Любая ветвь ненаправленного графа энергетической цепи соединяется с узлами разного типа. Модели узлов, в которых сходится большее количество ветвей, получаются каскадированием трехвыводных узлов. В динамике, поток (физическая величина первого рода) любой ветви входящей в узел может менять свое направление; в узлах графа происходит лишь смена знака потока.
Ветвь ненаправленного графа
Участок энергетической цепи в ненаправленном графе с одним и тем же потоком материи (координатой первого рода), который может состоять из произвольного количества последовательно включенных моделей физических элементов.
Контур
Для направленных и ненаправленных графов, это замкнутый путь, проходящий через несколько узлов и ветвей.
Координата первого рода (through variable3)
Отражение в модели той из парных физических величин (чье произведение есть мощность), которая фиксируется датчиком, установленным в разрыв любого подвода энергии к модулю динамической системы.Во всех энергетических доменах физические величины первого рода подчиняются первому закону Кирхгофа.
Координата второго рода (across variable3)
Отражение в модели той из парных физических величин (чье произведение есть мощность), которая фиксируется датчиком, подключенным между любыми двумя подводами энергии к модулю динамической системы. Во всех энергетических доменах физические величины второго рода подчиняются второму закону Кирхгофа.
Графический интерфейс программ математического моделирования динамических систем
Графический интерфейс — это самое "слабое место" программ математического моделирования динамических систем. Попробуем разобраться с тем, что может понимать русскоязычный специалист под скромным английским термином диаграмма (diagram), если с помощью неё требуется представить описание модели системы на том или ином уровне в графической форме:
Блок-схемы или около десятка именованных направленных графов.
Схемы физические принципиальные электрических, магнитных, тепловых, гидравлических, акустических, механических, ротационных, и др. цепей преобразования энергий. Они же ненаправленные или би(со)направленные графы.
Гибридные карты состояния или импульсные потоковые графы, графы переходных состояний.
Графы алгоритмов программ.
Структурные схемы, функциональные схемы, мнемосхемы.
И многое другое.
Разнообразие впечатляет. Однако цель перечисления не в потрясении воображения читателя, а в том, чтобы подвести к мысли о том, что задача создания графического интерфейса непроста и не соответствует квалификации разработчиков моделирующих программ. Конечный пользователь должен понимать, что без кооперации усилий нескольких фирм эту задачу не решить (спрос пользователя рождает предложение). С задачей качественного отображения всего перечисленного, в любых масштабах, на любых устройствах ввода вывода, могут справиться лишь редакторы векторной графики — это их прямая задача. Дополнительным требованием к претенденту на её выполнение является открытость объектной архитектуры и наличие документации.
Как бы ни было велико разнообразие способов графического описания моделей, четко просматриваются лишь две техники моделирования: структурное моделирование и мультидоменное физическое моделирование. Для поддержки структурного моделирования требуется решатель систем дифференциальных уравнений и блок-схемы [3]. Для поддержки мультидоменного физического моделирования требуется итерационный решатель систем алгебро-дифференциальных уравнений и схемы физические принципиальные [4]. Другие виды графов либо мало эффективны, либо являются предками направленных и ненаправленных графов соответственно. Моделирование же управляемое событиями не является новой техникой моделирования, а лишь дополняет названные совокупностью методов переключения и синхронизации фрагментов моделей в процессе симуляции, обеспечивая тем самым программный контроль над потоком. Т.е. программный контроль над процессом прогонки массива MathBlock[i] или его фрагментов в режиме симуляции:
Листинг 3
Пока (не случилось любое событие) Циклически исполнять фрагмент модели
for (i=0; i < numBlock-10; i++) MathBlock[i]->Calc(); Если (случилось такое событие) Исполнить фрагмент модели
for (i=numBlock-10; i < numBlock; i++) MathBlock[i]->Calc(); ... ' Использован синтаксис языка Си, дабы не усложнять список интерфейсов в табл. 2
Идея мультидоменного физического моделирования
Существуют фундаментальные физические постулаты. Первый постулат гласит, что материя не может появиться ни откуда и не может исчезнуть в никуда. Второй постулат утверждает то же самое в отношении энергетического потенциала. Эти постулаты имеют частные формулировки для каждого энергетического домена. Например, для электрического домена это первый и второй законы Кирхгофа.
Каждый из энергетических доменов характеризуется двумя физическими величинами первого и второго рода (их произведение всегда есть мощность). В случае электрического домена – это электрические ток и напряжение соответственно. Эти парные физические величины, в каждом энергетическом домене, связаны между собой законом Ома в соответствующей формулировке.

Демонстрируется система подобий между энергетическими доменами. Формулы для расчета мощности приведены с целью указания тех парных физических величин первого и второго рода, которые определяют вид закона Ома для соответствующего энергетического домена
Таким образом, в каждом из энергетических доменов потребителями энергии являются электрическое, магнитное, тепловое, гидравлическое, акустическое, механическое, ротационное и др. сопротивления. Во всех случаях это простые физические устройства, подразделяемые по принципу действия на три класса (R, L, C). Можно сказать, что для семи названных энергетических доменов закон Ома имеет 21 формулировку. Формулы закона Ома записываются тремя способами:
Электрические элементы

Три формы записи закона Ома определяют три формальных примитива, которые являются пассивными элементами ненаправленных графов, т.е. моделями потребителей энергии. В каждом из энергетических доменов для них существуют собственные условные графические обозначения, однако математическая суть соответствующих библиотечных элементов неизменна:
Гидравлические элементы

Тепловые элементы

Магнитные элементы
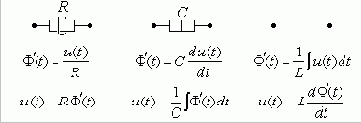
Механические элементы

Ротационные элементы

Девять формальных примитивов ненаправленных графов – потребители энергии, источники, узлы и заземлитель потенциала – позволяют разработать универсальную библиотеку элементов физических устройств любого масштаба и уровня детализации.
Резюме: Идея мультидоменного физического моделирования заключена в том, что модель любого технического устройства строится как преобразующая энергию цепь. В распоряжении пользователя предоставляется библиотека элементов физических устройств разных энергетических доменов. При этом вне зависимости от природы преобразуемой энергии, все библиотечные элементы подобны и строятся в соответствии с законом Ома и постулатами о сохранении материи и энергетического потенциала (первый и второй законы Кирхгофа).
Идентификация моделей
Рабочие файлы: [ABCD.vsm]
Идентификация компьютерных моделей
Та или иная алгоритмическая процедура, в результате выполнения которой моделирующая программа получает численные значения коэффициентов модели, структура которой и параметры были выбраны пользователем произвольно. Искомые коэффициенты могут быть представлены либо в форме ABCD-матриц, либо в форме коэффициентов полиномов числителя и знаменателя передаточной функции. Цель поиска коэффициентов состоит в предоставлении исходных данных для частотного, корневого и других видов анализа.
Аналитическая процедура приведения направленного графа сложна для программной реализации. По этой причине библиотеки анализа программ математического моделирования не отслеживают ни схему соединений блоков, определяемую пользователем, ни их параметры. Т.е. подобная информация для идентификации модели им не нужна (см. рис.1).

Легко увидеть, что в целях унификации вычислительных алгоритмов моделирующих программ можно объединить матрицы A, B, C и D, а так же матрицу U с координатой x, и матрицу U' с координатой y, как показано на рис. 2.

Рис. 3
Теперь, возвращаясь к процедуре идентификации, можно описать сценарий работы библиотеки анализа, конечной целью которого является идентификация коэффициентов модели:
Моделирующая программа для всех интеграторов модели (см. рис. 1) отключает вызов функции численного интегрирования, и, к освободившимся входам и выходам блоков 1/S, подключает библиотеку анализа. Дополнительными точками подключения библиотеки являются входная и выходная координаты модели. Библиотека анализа использует выходы блоков интеграторов для задания возмущений на граф модели, а их входы для фиксации отклика графа.
В момент подключения (инициализации) библиотека анализа создает будущий (искомый) "образ модели" в виде обнуленной ABCD-матрицы.
Далее, моделирующая программа инициирует процесс спец-симуляции модели длинной в n+1 шаг (на данном этапе функционирования, программы не используют графический интерфейс, т.е. скрывают свои действия от пользователя).
На каждом шаге спец-симуляции, библиотека анализа поочередно устанавливает на выходе одного из интеграторов модели единицу (другие возмущения обнуляются), и фиксирует реакцию графа.
Используя полученную совокупность отдельных реакций графа, библиотека анализа заполняет столбцы объединенной ABCD-матрицы в искомом "образе модели". Суть этой операции поясняет рис. 3.
Описанный сценарий легко поддается алгоритмизации и реализован в большинстве программ математического моделирования с поточной моделью управления. Следует отметить, что он может быть использован для идентификации мультичастотных дискретных, гибридных, а так же непрерывных систем со звеньями чистого запаздывания. В этом случае список блоков, к которым должна подключаться библиотека анализа расширяется регистрами задержки 1/Z
и звеньями чистого запаздывания e -ts. Но, составляя вектор задания, библиотека анализа должна хранить информацию о том, каким устройством формируется та или иная координата модели и его параметры (Tц для 1/Z и t
для e -ts), что требуется для процедуры расчета частотных характеристик.
Импульсные системы
Система импульсная линейная
Линейной системой импульсного регулирования называется такая САР, которая кроме звеньев описываемых обыкновенными линейными ДУ содержит импульсное звено, преобразующее непрерывное входное воздействие в равноотстоящие друг от друга по времени импульсы.
Инструкции
Данное руководство - это электронная версия документа tau.doc или tau_a5.doc. Назначение электронной версии - быстрый и систематизированный доступ во время занятий к тексту пособия, к изучаемым моделям, а так же, при необходимости, к конспекту лекций, и к тестам. Операционная система установленная на компьютерах должна распознавать расширения рабочих файлов (*.vsm и *.ca4) и, при активации в руководстве соответствующих гипертекстовых ссылок, должна автоматически запускать приложения VisSim и Electronics Workbench. Информация о версиях пакетов, их изготовителях и архиве моделей приведена в разделе "Требуемые программные пакеты". Достаточно, если студенты будут проинструктированы о порядке запуска электронного руководства (tau_knv.chm).
Интегральное регулирование
Интегральный закон регулирования имеет вид:
u(t) = Wрег(p) x(t) = k2/p x(t) ,
тогда в разомкнутом состоянии система будет характеризоваться ПФ:
W(p) = Wрег(p) Wo(p) = k2/p Wo(p) .
Рассмотрим уравнение ошибки:

В установившемся режиме p®0, => W(p)®Ґ; => первая составляющая ошибки g0/Ґ®0. Ошибка от возмущения зависит от вида функции Wf(0) и может быть отлична от нуля.
Резюме: I-регулирование позволяет исключить статическую ошибку в системе, т.е. система будет астатической по отношению к задающему воздействию g(t).
Интегральное регулирование по второму интегралу от ошибки
Двойной интегральный закон регулирования имеет вид:
u(t) = Wрег(p) x(t) = k3/p2 x(t) ,
тогда в разомкнутом состоянии система будет характеризоваться ПФ:
W(p) = Wрег(p) Wo(p) = k3/p2 Wo(p) .
В этом случае система будет обладать астатизмом второго порядка - в ноль обратятся как постоянная составляющая ошибки, так и её скоростная составляющая (ошибка от помехи здесь не рассматривается):

Резюме: повышение порядка астатизма приводит к увеличению установившейся точности САР, но делает систему более замедленной в действии.

На рисунке показано, что, на сколько бы мал ни был коэффициент усиления пропорционального канала, и насколько большим бы ни был коэффициент усиления интегрального канала, для малых отклонений ошибки x(t) сигнал управления на объект u(t) интегральным каналом формируется менее интенсивно.
Интегральные оценки качества
Рабочие файлы: [ok_absx_s.vsm]
Интегральные оценки дают обобщенную оценку быстроты затухания и величины отклонения регулируемой величины, в виде единого числового значения.
Находят применение первые три ИТ-оценки из перечисленных в списке:
I1 и I2 - линейные ИТ-оценки (не чувствительны к высшим производным координат САР).
I и I' - квадратичные ИТ-оценки (первая не чувствительна к высшим производным координат САР; вторая – к неподвижному режиму).
I+T12I' - улучшенная квадратичная ИТ-оценка (чувствительна к постоянной и к скоростной составляющим в движении координат САР).
I+T12I'+T24I''+... - ИТ-оценки более высоких порядков (чувствительны к постоянной составляющей в движении координат САР, к их скорости, к ускорению, ...).


Рассмотрим линейные ИТ-оценки:

Очевидно, что чем меньше значение оценки I1 или I2, тем лучше переходный процесс, но:
Оценка I1 не может применяться к колебательному переходному процессу.
Аналитическое вычисление оценки I2 по коэффициентам уравнения ошибки затруднено.
Одно значение оценки I2 может соответствовать переходным процессам с разной колебательностью (если совпадают мажоранты и миноранты).


Заметим, что оценку I' можно получить нахождением оценки I, если подать на вход САР не ступенчатую 1(t), а дельта функцию
d(t)=1'(t). Применение оценки I' ограничено тем, что она не чувствительна к установившемуся значению ошибки xҐ.
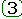
I и I' снимаются улучшенной квадратичной ИТ-оценкой:

где: x0 - начальное значение отклонения в переходном процессе; I+T12I'
– не формула, а составной символ обозначения данной ИТ-оценки.
Очевидно, что I+T12I'
будет минимальна при T1x'+x = (T1p+1)x = 0. Решение этого ДУ есть экспонента:


Т.е. улучшенная квадратичная ИТ-оценка I+T12I'
будет иметь минимум при приближении переходной функции к экспоненте с заданной постоянной времени T1.


Здесь оценка будет иметь минимум, только при перемещениях координат САР с определенными скоростью и ускорением, которые задаются постоянными времени T1 и T2 соответственно. Идея другого способа выбора параметров оценки заключена в том, что коэффициенты ДУ второго порядка можно выразить в виде затухания z и резонансной частоты q, которыми должна обладать настраиваемая САР.
