Автоматическое регулирование момента в системе УП-Д

Общий анализ свойств регулируемого электропривода, замкнутого отрицательной обратной связью по электромагнитному моменту, целесообразно провести с помощью обобщенной структурной схемы на рис.6.15,б, дополнив ее цепью указанной обратной связи. При этих условиях структурная схема имеет вид, показанный на рис.7.9, и позволяет записать следующую систему уравнений механической характеристики электропривода:

Путем преобразования системы (7.22) получим уравнение механической характеристики электропривода в виде зависимости момента от скорости:

Уравнение статической механической характеристики получим из (7.23) при р=0:

где

- момент короткого замыкания;  - модуль статической жесткости; w0зм=uзмk'П - скорость идеального холостого хода в замкнутой системе регулирования.

Примем, что необходимо получить при w=0 заданное значение момента стопорения электропривода Мк 3=Мстоп. Это значение может быть получено при различных коэффициентах обратной связи по моменту путем выбора соответствующих значений U3M с помощью соотношения

Семейство механических характеристик электропривода, соответствующее Мк3=Мстоп=const при k0м=var, приведено на рис.7.10,а. Рассматривая его, можно установить, что статическая точность регулирования момента в данной схеме при прочих равных условиях ограничена сильным возмущающим воздействием, оказываемым электромеханической связью Вследствие действия этой связи изменения скорости двигателя в замкнутой системе регулирования оказывают на момент тем более значительное влияние, чем меньше коэффициент обратной связи по моменту. При возрастании k0M жесткость статической характеристики уменьшается и при неограниченном возрастании kOM или k'п стремится к нулю. Однако при реальных значениях этих величин исключить существенное влияние изменений скорости на точность регулирования момента без принятия специальных мер практически невозможно.

При отсутствии обратной связи по моменту (k0м=0) для получения момента Мстоп необходимо небольшое значение задающего сигнала U3ом.
Увеличение kOM приводит к соответствующему возрастанию Uзoм и задаваемой преобразователем скорости идеального холостого хода w0зм- Поэтому при больших коэффициентах обратной связи на форме характеристик двигателя сказывается ограничение выходной переменной преобразователя, обусловленное в системе Г-Д насыщением магнитной цепи генератора и ограниченностью максимального напряжения возбуждения, в системе ТП-Д - необходимым ограничением предельных углов регулирования реверсивного преобразователя в выпрямительном и инверторном режимах и напряжением сети, а в системе ПЧ-АД - ограничением максимальной частоты. Если представить характеристику преобразователя линейной зависимостью w0=f(Uуч) с идеальным ограничением максимального значения w0 величиной w0max, то легко установить, что пределы изменения скорости, в которых с помощью отрицательной связи по моменту обеспечивается с той или иной точностью регулирование момента, ограничены сверху и снизу характеристиками разомкнутой системы, соответствующими w0=±w0max=const (рис.7.10,а).

В электроприводах постоянного тока вместо обратной связи по моменту обычно используется обратная связь по току якоря, действие которой при Ф=Фном=const вполне аналогично рассмотренному При этом в полученных соотношениях коэффициент k0м может быть выражен через коэффициент отрицательной связи по току якоря

При конечных значениях коэффициентов усиления kп' и обратной связи kOM

эффективным средством уменьшения зависимости момента от скорости является использование формирующей положительной обратной связи по скорости двигателя, т.е. компенсационного принципа, в дополнение к основной системе регулирования по отклонению. Цепь формирующей положительной связи по скорости показана на рис.7.9 штриховой линией. Уравнение статической характеристики электропривода при введении этой связи можно получить из соотношений



где kn c - коэффициент положительной связи по скорости. Откуда



Модуль статической жесткости механической характеристики в замкнутой системе зависит от коэффициента формирующей обратной связи по скорости:





При увеличении knc модуль статической жесткости быстро убывает и при критической положительной связи по скорости kпскр=1/k'n становится равным нулю. Дальнейшее увеличение kn c приводит к изменению знака жесткости, как это показано на рис.7.10,б. При критической положительной связи статическая ошибка, обусловленная изменениями скорости, исключается, и система обеспечивает астатическое регулирование момента без введения в цепь регулирования регуляторов с интегральной характеристикой.

Сочетание компенсационного принципа с регулированием по отклонению дает комбинированную систему управления, обеспечивающую высокую статическую точность регулирования наиболее простым путем. С помощью уравнения (7.23) при uзм=0 получим уравнение динамической жесткости механической характеристики в замкнутой системе:



При безынерционном преобразователе Тп=0 выражение (7.28) принимает вид



где

Уравнение (7.29) по форме совпадает с выражением динамической жесткости в разомкнутой системе УП-Д, а анализ его параметров показывает, что при Тп=0 отрицательная обратная связь по моменту влияет на характеристики электропривода так же, как введение резистора в цепь якоря двигателя постоянного тока. Модуль жесткости bзм при этом уменьшается и одновременно уменьшается эквивалентная постоянная времени Tэзм.

На рис.7.11,а приведены ЛАЧХ и ЛФЧХ динамической жесткости, построенные по (7.29), которые подтверждают сказанное. Динамическая жесткость в замкнутой системе при Тп=0 (кривые 1 и 1') снижается во всем диапазоне частот относительно жесткости в разомкнутой системе (кривые 2 и 2'), при этом точность регулирования момента в широком диапазоне частот остается высокой и ошибки регулирования с ростом частоты снижаются.

В случае когда Тп>>Тэ, выражение (7.28) можно представить:



где Tп э - эквивалентная постоянная времени преобразователя в замкнутой системе, Тпэ=Тп/(1+bekOMk'п), если приближенно принять (Tп+Tэ)/(1+bekOMk'п)»Тпэ+ Тэ при Тп>Т3.

Соответствующие (7.30) ЛАЧХ и ЛФЧХ динамической жесткости замкнутой системы представлены на рис.7.11,б.


Они свидетельствуют о том, что при большой Тп высокая точность регулирования момента имеет место лишь при низких частотах, а в области средних и высоких частот динамические свойства замкнутой системы электропривода аналогичны динамическим свойствам разомкнутой системы. Таким же путем можно убедиться, что введение формирующей положительной связи по скорости влияет на вид ЛАЧХ и ЛФЧХ только в области низких частот, т. е. сказывается в основном на статической точности регулирования момента. Для анализа влияния обратной связи по моменту (току) на колебательность электропривода при жестких механических связях структурную схему рис.7.9 с помощью (6.28) полезно представить в виде, показанном на рис.7.12. Колебательность электропривода при Тп»О оценим с помощью характеристического уравнения замкнутой системы, которое можно получить из передаточной функции замкнутого контура на рис.7.12 при Мс=0 в виде



Нетрудно видеть, что при Тп=0 регулируемый по моменту электропривод представляет собой колебательное звено



где

Введение отрицательной связи по моменту увеличивает Тмзм и уменьшает Тэзм при этом соотношение постоянных m изменяется в сторону меньшей колебательности, а быстродействие по моменту в связи с уменьшением Гэзм увеличивается. Как следствие, необходимости коррекции контура регулирования момента при Тп=0 не возникает.

Учет инерционности преобразователя (Тп¹0) увеличивает порядок характеристического уравнения системы, что затрудняет оценку колебательности по его корням. Динамические свойства электропривода, замкнутого обратной связью по моменту, удобнее проанализировать по соответствующей ЛАЧХ разомкнутого контура:



При Тп>>Тэ в структуре на рис.7.12 звено динамической жесткости можно приближенно представить в виде (7.30) вместо (7.28), при этом



Соответствующая (7.34) ЛАЧХ показана на рис.7.13. Анализируя (7.34) и рис.7.13, можно установить, что при небольших Тм и Tп, а также при больших Тп и сильной отрицательной связи по моменту (Тп э»Тэ) частота среза может находиться в области асимптоты с наклоном -40 дБ/дек и качество регулирования момента может быть неудовлетворительным.

Поэтому обычно при автоматическом регулировании момента электропривода требуется коррекция динамических свойств тем или иным способом. Без коррекции удается обойтись только в тех случаях, когда требования к быстродействию и точности регулирования момента и тока в динамике невысоки. При этом необходимая точность регулирования в статике обеспечивается введением критической положительной связи по скорости (или по напряжению генератора в системе Г-Д), а отрицательная связь по моменту (току) ослабляется до уровня, обеспечивающего требуемое демпфирование переходных процессов.

Автоматическое регулирование положения по отклонению

Автоматическое регулирование положения требует измерения углового или линейного перемещения рабочего органа механизма и использования устройств, задающих эти перемещения.

В простейшем варианте автоматическое регулирование положения предусматривается лишь на участках движения в районе заданных рабочих позиций, а на основной части пути перемещения от позиции к позиции система по выходной координате разомкнута. Этот вариант позволяет использовать индуктивные датчики ошибки позиционирования, вырабатывающие сигнал, пропорциональный отклонению рабочего органа от заданного положения. Датчики подключаются в зоне точного останова. Они обеспечивают автоматическое регулирование положения по отклонению от заданной точки пути с требуемой точностью.

При необходимости отработки дозированных перемещений, задаваемых на входе системы скачком, или при осуществлении программного управления перемещением рабочего органа механизма необходим постоянный контроль текущего положения, осуществляемый датчиками углового или линейного перемещения непрерывного или дискретного действия.

В данной главе ограничимся рассмотрением электроприводов постоянного тока, механическая часть которых с удовлетворительной точностью может быть представлена жестким механическим звеном, приведенным к валу двигателя. Для электроприводов позиционных механизмов кроме регулирования положения обычно требуются регулирование скорости и ограничение тока якоря в переходных процессах допустимым значением Iя=Iстоп. Поэтому в качестве объекта регулирования положения примем однократноинтегрирующую систему регулирования скорости в системе ТП-Д с подчиненным контуром регулирования тока. Дополнив ее интегрированием скорости w для получения перемещения f, введя обратную связь по положению с коэффициентом усиления ko.п и включив на вход регулятор положения, получим трехконтурную систему регулирования положения, структурная схема которой приведена на рис.9.4.

Осуществим оптимизацию контура регулирования положения методом последовательной коррекции, определив необходимую для этой цели передаточную функцию регулятора положения.
В соответствии с рис.9.4 объект регулирования положения в данном случае имеет следующую передаточную функцию:

Для получения передаточной функции разомкнутого контура регулирования положения вида

 

регулятор положения должен иметь передаточную функцию



Передаточная функция замкнутого контура регулирования положения



Проведем качественный анализ работы синтезированной системы регулирования положения при различных условиях. Сначала будем полагать, что система автоматического регулирования положения замыкается при подходе к зоне точного останова электропривода в целях увеличения точности позиционирования. В момент замыкания системы электропривод движется с начальной установившейся скоростью wнач и датчик положения выдает сигнал ошибки Df'нач, равный расстоянию от начальной точки до заданной позиции f'з. При настройке контура на критическое демпфирование (ап=4) и отсутствии статической нагрузки (Мс=0) переходный процесс точного позиционирования будет иметь характер, показанный на рис.9.5,а. На этом рисунке приведены зависимости Dф, w и iя=f(t). соответствующие сформулированным начальным условиям. Для анализа этих зависимостей обратим внимание на то, что выходное напряжение регулятора положения в данной схеме представляет собой сигнал задания скорости



С помощью (9.13) можно определить задаваемый на входе контура регулирования скорости темп замедления в процессе отработки сигнала ошибки Dф':



Таким образом, задаваемое регулятором положения максимальное ускорение электропривода в процессе замедления тем больше, чем больше начальная скорость wнач. Так как wнач»w3нач, то из (9.13) следует, что при данном коэффициенте усиления kpп, определяемом (9.11), максимальное ускорение в процессе замедления возрастает с возрастанием отрабатываемого перемещения Dfнач.

Соответственно возрастает и максимальный ток якоря Imax, который в соответствии с уравнением движения равен



До тех пор пока задаваемое перемещение при замыкании системы невелико и Imax<IСТОП, система остается линейной, обеспечивая требуемое качество регулирования.


Если Df'нач и соответственно wзнач и wнач настолько велики, что Imax>IСТОП, регулятор скорости переходит на насыщенный участок своей характеристики, выдавая Uзт=Uзтmax=kотImax=const. система регулирования положения размыкается, и идет процесс замедления с iя»Iстоп=const Так как ускорение, соответствующее стопорному моменту, меньше задаваемого, накапливается дополнительная ошибка регулирования положения, которая в конце процесса отрабатывается с перерегулированием

Из изложенного следует, что оптимизированный контур регулирования положения (kpп=kpпо) требует ограничения отрабатываемого перемещения и ограничения начальной скорости в момент замыкания системы допустимыми значениями, при которых ток якоря в процессе замедления не достигает стопорного значения Определим с помощью (9.14) и (9.15) допустимое значение скорости электропривода в момент максимума тока якоря tmax(dwз/dt=-eтmax)



Кроме того, если примем время нарастания тока до максимума tmax»2aтTm, получим:




Следовательно,

Таким образом, и при использовании для увеличения точности позиционирования автоматического регулирования положения в зоне точного останова для нормального функционирования системы необходимо снижать скорость при подходе к этой зоне до значения, определяемого (9.18) Из (9 18) следует, что тормозной момент нагрузки увеличивает допустимое значение начальной скорости; поэтому, если нагрузка изменяется в широких пределах, эту скорость нужно определять по минимальному значению Мс.

Аналогичные условия складываются и в тех случаях, когда система регулирования положения предусматривается для отработки различных дозированных перемещений, задаваемых на входе системы В этом случае цикл перемещения начинается при нулевых начальных условиях и, как показано на рис 9 5,б, состоит из участка ускорения электропривода до скорости wmax и участка замедления его с остановом в заданной точке пути Чем больше заданное перемещение Df'з, тем больше максимум тока при пуске, тем больше максимум скорости wmax и тем больше максимальный ток в процессе замедления Imax.


Поэтому и здесь оптимальные динамические свойства системы регулирования положения сохраняются только в пределах тех задаваемых перемещений Df'з, при которых в процессах замедления она остается линейной (Imax<Iстоп). При этом wmax оказывается значительно меньше номинальной рабочей скорости wном, следовательно, ограничить uзс значением kocwmax в данном случае нельзя.

Избежать дополнительного перерегулирования при торможении с максимальной рабочей скорости wp.max можно, подобрав такой коэффициент усиления регулятора положения, при котором в момент перехода на торможение в соответствии с (9.13) задается номинальная рабочая скорость электропривода при рассогласовании, равном максимальному пути торможения со скорости wном при |eср|=eтmax=const:



Подставив (9.19) в (9.13), разрешим полученное уравнение относительно kpn=kpn1:



Выбор коэффициента усиления регулятора положения по условию (9.20) позволяет получить удовлетворительное качество регулирования при задании перемещений, которым соответствует начальная скорость при торможении, равная wном. Однако при отработке перемещений, при которых начальная скорость при торможении оказывается меньше wном, процессы торможения сопровождаются дотягиванием, причем их длительность остается такой же, как и при отработке больших перемещений. В связи с этим для подобных электроприводов используют регулятор положения с параболической характеристикой. Примем, что при максимальном перемещении Df'т.max коэффициент усиления регулятора положения kрп был равен (9.20) и при меньших перемещениях изменялся бы обратно пропорционально w:



В процессе замедления с постоянным ускорением eтmax скорость w связана с рассогласованием аналогично (9.19):



Определив из (9.22) w и подставив это выражение в (9.21), получим



Выходное напряжение регулятора положения U3C с входным сигналом рассогласования Dф' должно быть связано соотношением



Зависимость Uзс=f(Dф'), соответствующая (9.24) представлена на рис.9.6 (кривая 1). При Dф'=Dфтmax коэффициент kpn имеет значение





т. е. такое же, как и при линейном регуляторе с коэффициентом усиления kрп1 (9.20).

На рис.9. 6 показаны характеристики регулятора, соответствующие (9.20) - прямая 2 и (9.25) - прямая 3, причем показано ограничение заданного значения скорости U3C=kосwном. Уменьшение Dф' в соответствии с (9.23) приводит к увеличению коэффициента регулятора вплоть до оптимального значения, определяемого (9.11). Это значение имеет место при Dф'=Dф'нач.доп, и ему соответствует характеристика 3 на рис.9.6. В этом можно убедиться, подставив в (9.21) значения w=wmaxдоп из (9.16). При дальнейшем уменьшении Dф'<Dф'нач.доп увеличение kpп по (9.23) привело бы к увеличению колебательности. Поэтому нелинейная зависимость Uзс=f(Dф') имеет вид жирной кривой 1, которая при DФ'<Dф'нач.доп совпадает с прямой 3, при Dф'нач.доп<Dф'<Dф'т.max определяется (9.23), при Dф'>Dф'т.max ограничена значением U3c.max=const. Для рассмотренных систем основным требованием, предъявляемым к электроприводу в отношении точности регулирования, является требование ограничения статической ошибки позиционирования заданным допустимым значением. В связи с наличием интегральной составляющей передаточной функции регулятора тока в установившемся режиме напряжение на его входе равно нулю:



Подставив в (9.26) выражения kрс из (8.39) и kpn=kрпо из (9.11), получим статическую ошибку в оптимизированной системе



Следовательно, статическая ошибка позиционирования



Если коэффициент усиления регулятора kpn=kpn1 (9.20), ошибка позиционирования возрастает во столько раз, во сколько kpn1 меньше kрпо (рис.9.6):



Необходимость использования регулятора положения с нелинейной характеристикой может быть исключена при любых перемещениях путем задания на входе системы требуемого закона ф'3=f(t), при отработке которого система остается во всех режимах линейной. Для подобных систем автоматического программного регулирования положения характерны более высокие требования к динамической точности регулирования, которые аналогичны требованиям к следящему электроприводу, особенности которого кратко рассмотрены ниже.

Автоматическое регулирование скорости в системе УП-Д

Возможный диапазон регулирования скорости изменением напряжения на якоре двигателя или частоты в системе УП-Д может быть многократно расширен путем автоматического регулирования скорости по отклонению от заданного значения. Рассмотрим, как изменяются свойства электропривода при замыкании электромеханической системы отрицательной обратной связью по скорости. Анализ проведем применительно к обобщенной системе УП-Д при с12=¥. Структурная схема регулирования скорости приведена на рис.8.8. Данной схеме соответствуют следующие уравнения, описывающие механическую характеристику регулируемого электропривода:

В результате преобразований (8.24) получим уравнение механической характеристики электропривода в виде

При р=0 уравнение (8.25) представляет собой уравнение статической механической характеристики

рассматривая которое, можно установить, что с увеличением коэффициента обратной связи по скорости k0 c при прочих равных условиях уменьшается скорость идеального холостого хода и возрастает жесткость механической характеристики. Сказанное поясняется статическими характеристиками, представленными на рис.8.9, где показано, что при неизменном задающем сигнале в разомкнутой системе (Uзс=U30), обеспечивающем номинальную скорость электропривода в разомкнутой системе (kос=0), введение отрицательной связи с коэффициентом koc=koc1 снижает скорость идеального холостого хода, но существенно увеличивает жесткость. Для получения номинальной скорости задающий сигнал должен быть увеличен до U3C=U3c1> U30.

Чем выше коэффициент обратной связи koc, тем большее напряжение U3C требуется для получения той же скорости и тем меньше ошибка регулирования, обусловленная изменениями статической нагрузки. Статизм при данном коэффициенте обратной связи уменьшается с возрастанием коэффициента усиления k'n, и теоретически при k0ck'п®¥ статическая ошибка регулирования стремится к нулю.

Положив в (8.25) uзс=0, получим выражение динамической жесткости механической характеристики электропривода в замкнутой системе

где - коэффициент увеличения модуля жесткости в замкнутой системе bзс по сравнению с bе. При Тп=0 уравнение амплитудно-частотной характеристики динамической жесткости имеет вид



а фазочастотная характеристика не зависит от koc и определяется соотношением Y(W)=-p-arctg ТэW, соответствующим разомкнутой системе. Нетрудно видеть, что модуль динамической жесткости при любой частоте в k=bзс/bе раз больше модуля динамической жесткости в разомкнутой системе при той же частоте. Фазовый сдвиг между колебаниями скорости и моментадвигателя остается постоянным при данной частоте для любых значений koc (рис.8.10,a).

При Тп>>Тэ уравнению (8.27) соответствуют частотные характеристики динамической жесткости,приведенные на рис.8.10,б. Увеличение коэффициента обратной связи по скорости при этом увеличивает модуль динамической жесткости только в низкочастотной области. При W>1/Тп модуль жесткости быстро уменьшается, и при W>1/Тпэ= =kуж/Тп асимптотическая ЛАЧХ сливается с такой же частотной характеристикой разомкнутой системы (kос=0).

Как уже отмечалось, при заданных параметрах механической части динамические свойства электропривода определяются передаточной функцией динамической жесткости механической характеристики Проследим эту взаимосвязь при автоматическом регулировании скорости.

С этой целью преобразуем структурную схему на рис.8.8 так, чтобы иметь одну единичную обратную связь по скорости (рис.8.11). Нетрудно видеть, что при этом связь момента с изменениями скорости при uзс=const определяется передаточной функцией - bдинзс(р) (8.27), что при жестком механическом звене определяет передаточную функцию разомкнутого контура регулирования в виде



При Tп=0 (8.29) запишем в виде





Частотные характеристики Lw(W), соответствующие (8.30), представлены на рис.8.10,в во взаимосвязи с ЛАЧХ динамической жесткости при Тп=0, показанными на рис.8.10,а. Увеличение коэффициента обратной связи kос приводит к увеличению bзс в диапазоне частот 0<W<1/Тэ, что влечет за собой смещение частоты среза W для системы при koc¹0 в область более высоких частот на участок с наклоном -40 дБ/дек.


Очевидно, это вызывает быстрое ухудшение динамических показателей качества регулирования. Фазочастотная характеристика электропривода Yw(Ф) при этом не зависит от koc, так как в разомкнутой и замкнутой системах фазочастотные характеристики динамической жесткости Yb(W) одинаковы (рис.8.10,a).

Вывод об увеличении колебательности вытекает непосредственно из рассмотрения (8.30), так как увеличение koc и kуж уменьшает Tмзс=TM/kуж. Отношение постоянных mзс=ТМЗС/ТЭ уменьшается, что и приводит к быстрому возрастанию колебательности. Малая постоянная времени быстродействующего преобразователя при этом является фактором, дополнительно снижающим запас по фазе на частоте среза, что ухудшает качество регулирования вплоть до возможной неустойчивости контура.

Большая постоянная времени преобразователя Тп>>Тэ, например, в системе Г-Д влияет на динамику регулирования несколько иначе. Частотные характеристики разомкнутого контура для этого случая показаны на рис.8.10,г, которые также следует сопоставить с соответствующими ЛАЧХ bдинзс (рис.8.10,б). Здесь при увеличении koc и kуж возрастает частота сопряжения 1/Тпэ, что вызывает сужение участка с наклоном -20 дБ/дек в области частоты среза, однако частота среза Wc в разомкнутой системе (koc=0) и в системе замкнутой по скорости (kос¹0), остается неизменной, пока 1/Тпэ<Wc. Следовательно, если средне-частотная асимптота в области частоты среза сохраняет достаточно протяженный участок с наклоном -20 дБ/дек, динамические свойства электропривода остаются близкими таковым в разомкнутой системе. Сравнивая фазо-частотные характеристики Yw(W) при kос=0 и koc¹Q (рис.8.10,в), можно убедиться, что при 1/Tпэ<<1/Тэ запас по фазе на частоте среза в замкнутой системе незначительно снижается по сравнению со снижением в разомкнутой системе, причем изменения определяются изменениями в зависимости Yb(W) (рис.8.10,б). Если при этом Тм>Тэ, можно определить допустимое по качеству регулирования значение koc, задавшись шириной среднечастотной асимптоты.


Например, при условии Тп'=4·Тэ допустимый коэффициент обратной связи по скорости составляет



Более точно это значение можно определить, задавшись требуемым запасом по фазе на частоте среза разомкнутого контура.

При kос>(kос)доп значения Тпэ приближаются к Тэ, участок с наклоном -20 дБ/дек сужается и исчезает, что соответствует неустойчивости контура регулирования. Таким образом, хотя при Тп>>Гэ возможности регулирования несколько расширяются, однако и в этом случае отрицательная связь по скорости увеличивает колебательность электропривода по сравнению с разомкнутой системой.

На основании проведенного анализа свойств электропривода, замкнутого отрицательной связью по скорости, можно заключить, что без применения динамической коррекции получить высокую точность регулирования при требуемых динамических показателях качества регулирования в большинстве случаев невозможно.

Стремление повысить точность регулирования, не прибегая к сложной динамической коррекции системы, определяет целесообразность использования комбинированного способа управления - дополнения системы регулирования по отклонению компенсацией возмущения, обусловленного нагрузкой. Из возможных реализаций компенсации рассмотрим случай, когда с этой целью используется жесткая положительная обратная связь по моменту двигателя, показанная на рис.8.8 штриховой линией. Такая обратная связь наиболее просто осуществляется в системе ТП-Д или Г-Д, где при Фном=const М=c·iя, т.е. достаточно ввести положительную связь по току якоря. Комбинированной системе регулирования соответствуют следующие уравнения, описывающие механическую характеристику электропривода:



В результате преобразований (8.32) при Uзс=0 с учетом (8.27) получим выражение динамической жесткости механической характеристики электропривода в такой системе в виде



Уравнение (8.33) свидетельствует о том, что введение положительной связи по моменту увеличивает модуль статической жесткости в замкнутой системе, причем при bеkпмk'п=1 модуль статической жесткости возрастает до бесконечности, а уравнение (8.33) принимает вид





При значительной инерционности преобразователя (Тп>>Тэ) уравнение (8.34) можно упростить:



Сравнивая (8.35) с (8.27), можно установить, что при этих условиях положительная связь по моменту (току) бесконечно увеличивает модуль статической жесткости (b'3с=¥ при W=0) и незначительно сказывается на показателях качества регулирования. Действительно, при построении асимптотических ЛАЧХ динамической жесткости, соответствующих (8.35) и (8.27), выявляется, что при W>l/Tп (8.27) приближенно выражается соотношением (8.35). Это значит, что среднечастотная асимптота разомкнутого контура регулирования скорости при введении положительной связи по моменту не претерпевает существенных изменений и динамические показатели комбинированной системы регулирования определяются коэффициентами усиления и отрицательной связи по скорости. Выбирая koc из условия (8.31) и устанавливая критическое значение коэффициента положительной связи по моменту из условия bekПMk'п=1, можно исключить статическую ошибку по нагрузке электропривода при сохранении показателей качества регулирования, соответствующих условию (8.31).

Таким образом, в системе Г-Д положительная связь по току при Тг» Тя является эффективным средством увеличения статической точности регулирования. Динамическая точность регулирования при этом возрастает незначительно, так как уже при небольших частотах (W>1/Гп) амплитудно-частотная характеристика |b'дин зc(fW)| практически совпадает с такой же характеристикой при kПM=0.

При высоком быстродействии преобразователя (Тп=0) увеличение жесткости механических характеристик за счет положительной связи по моменту ухудшает качество регулирования так же, как и при регулировании по отклонению. При этом требуемые точность и качество регулирования скорости достигаются применением параллельной или последовательной коррекции.

Как было установлено, при отсутствии коррекции частота среза Wc в замкнутой системе при больших Тп остается близкой частоте среза при kос=0, которая определяется соотношением Wс=1/mТэ, при этом быстродействие электропривода по нагрузке определяется электромагнитной инерцией силовой цепи (Тэ) и отношением постоянных m=ТМ/ТЭ.


Объясняется это тем, что при высоких частотах большая постоянная Тп для внешней обратной связи по скорости является фильтром и свойства электропривода определяются внутренней, а не внешней обратной связью по скорости.

Быстродействие электропривода по управляющему воздействию зависит от Тп и koc. В этом можно убедиться, рассматривая структурную схему на рис.8.11. При скачке U3C скорость w0зс изменяется тем быстрее, чем меньше Тп и чем сильнее отрицательная обратная связь по скорости. В соответствии с уравнением


отрицательная связь по скорости оказывает форсирующее действие на замедленные инерцией преобразователя процессы: чем больше koc, тем больше при заданной скорости скачок U3C и начальное значение uy что при надлежащем запасе по напряжению управления преобразователя (uв в системе Г-Д) обеспечивает увеличение темпа изменения w0 и ускорение протекания переходных процессов.

Частотное регулирование момента асинхронного электропривода

Управляемость асинхронного электропривода, аналогичная управляемости электропривода постоянного тока при Uя=const и Ф=const, обеспечивается путем одновременного регулирования частоты f1 и напряжения U1 или тока I1 статорной обмотки.

Этот способ регулирования момента реализуется в системе ПЧ-АД, основные особенности которой были подробно рассмотрены в §6.5. При выполнении условий, для которых справедливо линеаризованное уравнение механической характеристики асинхронного двигателя при питании от источника напряжения (см. §3.11) и от источника тока (см. §3.12), при регулировании момента можно использовать структурную схему асинхронного электропривода, представленную на рис.6.14. Если, например, при поддержании постоянным потока Y1=const замкнуть систему отрицательной обратной связью по моменту М с коэффициентом обратной связи по моменту kом, асинхронный электропривод приобретет свойства, подробно рассмотренные для обобщенной системы УП-Д в §7.4.

Однако реализация рассмотренного там способа регулирования момента по отклонению в применении к асинхронному электроприводу вызывает практические трудности. Важной особенностью асинхронного электропривода является отсутствие простых способов измерения электромагнитного момента двигателя. Без принятия специальных мер, рассматриваемых в §8.9, момент асинхронного двигателя нелинейно зависит от доступного для измерения тока статора, и реализовать обратную связь по моменту с помощью связи по току, как в электроприводе постоянного тока, здесь не удается. Как следствие, во многих практических случаях от автоматического регулирования момента по отклонению отказываются и прибегают к использованию компенсационного способа управления с помощью положительной обратной связи по скорости. Как показано на рис.7.20,а и б, для измерения скорости на валу двигателя устанавливается тахогенератор ТГ, ЭДС которого eтг при постоянном потоке Фтг пропорциональна скорости:

при этом уравнение для канала регулирования частоты имеет вид

 (7.63)

где kp м - коэффициент усиления регулятора момента РМ.

В соответствии со структурной схемой на рис.7.11 при учете (7.63) можно записать



Подбором значений kp м и kп c обеспечивается критическая положительная связь по скорости



при этом уравнение механической характеристики запишется в виде



где

Разрешим (7.63) относительно uзм



С учетом (7.65) получим





Соотношение (7.67) свидетельствует о том, что в схемах на рис.7.20 сигнал задания момента пропорционален абсолютному скольжению двигателя sa, поэтому рассматриваемый компенсационный способ иногда называют управлением по абсолютному скольжению.

Механические характеристики w=f(М), соответствующие (7.66) при p=0, представлены на рис.7.21,д. Они построены в предположении, что преобразователь частоты обладает способностью рекуперации энергии в сеть. Если преобразователь не обеспечивает такой возможности, во втором и четвертом квадрантах механические характеристики существуют в узкой области, ограниченной осью абсцисс и характеристикой динамического торможения 2.

При преобразователе частоты, способном передавать энергию как в прямом, так и в обратном направлениях, при критической положительной связи по скорости обеспечивается астатическое регулирование момента в пределах, ограниченных перегрузочной способностью двигателя (M<Мк) и при изменении скорости от характеристики 1, соответствующей w0=w0max=const, до характеристики 3, соответствующей противоположному направлению вращения поля и максимальной частоте преобразователя частоты w0=-w0mах.

Перегрузочная способность Мк в данной схеме зависит от способа управления полем двигателя. Наименьшая перегрузочная способность соответствует регулированию при Y1=const, наибольшая - при Y2=const, причем она ограничивается насыщением магнитной цепи машины и запасом по напряжению преобразователя частоты как при питании от источника напряжения (см. рис.7 20,a), так и при питании от источника тока (см. рис.7.20,б).

В схеме с инвертором напряжения для регулирования потока в канале управления напряжением uун предусматривается функциональный преобразователь ФП, на вход которого подаются сигнал uуч, пропорциональный w0эл, и сигнал uзм, пропорциональный абсолютному скольжению sa.


В функции этих величин функциональный преобразователь определяет сигнал задания напряжения uун в при Y1=Y1ном=const или Y2=Y2нoч=const. В частности, при Y1=const сигнал uун=U1/kун вычисляется по соотношению (6.17а).

В схеме с инвертором тока (см. рис.7.20,б) в канал регулирования тока uут введено нелинейное звено Н31, которое формирует сигнал задания uут в нелинейной зависимости от sa, определяемой соотношением (6.176) при Y2=Y2max=const:



Для поддержания постоянным вектора потокосцеплсния  в динамике на рис.7.20,б у инвертора тока предусмотрен вход управления фазой тока f1. В канал регулирования фазы тока введено нелинейное звено Н32, реализующее зависимость от абсолютного скольжения, определяемую по (6.17в):



Динамические свойства электропривода с рассматриваемым способом регулирования момента определяются (7.66), которое вместе с уравнением движения позволяет построить структурную схему, представленную на рис.7.21,б.

Рассматривая эту структурную схему, можно заключить, что при задании момента скачком он нарастает до заданного значения М3=kмUзм по экспоненте и через (3¸4)TЭ устанавливается на заданном уровне М=М3=const Под действием постоянного момента электропривод при Мс=const движется равномерно ускоренно до тех пор, пока нарастающая частота f1(w0эл) не достигнет максимального значения f1max(w0злmax). Далее при f1=f1maх=const движение электропривода при данном моменте нагрузки Мс определяется механической характеристикой 1 (рис.7.21,а).

Динамические нагрузки электропривода

Правые части уравнений движения электропривода представ­ляют собой моменты действующих в системе сил инерции. В от­личие от рассмотренных выше моментов статической нагрузки электропривода, которые являются внешними воздействиями и не зависят от ускорений масс системы, силы и моменты сил инерции пропорциональны ускорениям масс:

Такие силы и моменты в теории электропривода принято на­зывать динамическими силами и моментами. Уравнение движения приведенного жесткого механического звена определяет суммар­ную динамическую нагрузку электропривода

которая при принятом правиле знаков численно равна результи­рующему моменту М-Мс, приложенному к движущимся массам.

Динамический момент является важной составляющей полной нагрузки электропривода. Он представляет собой алгебраичес­кую величину, знак которой при ускорении системы совпадает со знаком скорости, а при замедлении противоположен знаку скорости. При ускорении системы динамический момент являет­ся тормозным, и двигатель, преодолевая этот момент, совершает работу, затрачиваемую на увеличение запаса кинетической энер­гии системы. При замедлении системы, напротив, динамический момент является движущим Освобождающаяся при снижении скорости кинетическая энергия расходуется на совершение рабо­ты по преодолению результирующего момента М-Mс, который в этом случае является тормозным.

Как правило, для конкретных производственных механизмов бывает задано требуемое время пуска или расчетное ускорение eгр. Наибольший возможный статический и наибольший требуемый динамический моменты определяют максимум полной нагрузки и соответственно наибольшее значение электромагнитного момента двигателя, которое он должен создавать в процессе работы электропривода:

Значения Мmax определяют кратковременные перегрузки двигателя, которые не должны превышать допустимой перегрузочной способности двигателя.

Результирующий момент М-Мс (1.68) при пуске частично затрачивается на ускорение ротора двигателя и связанных с его валом элементов, а в остальной части через передачи воздействует на массы механизма, вызывая их ускорение и совершая работу по увеличению запасенной в них кинетической энергии.
Следовательно, динамическая нагрузка при пуске увеличивает полную нагрузку передач на значение динамического момента механизма J2·eср (см. рис.1.9):

При J2>>J1 это увеличение может быть значительным, а при J2<J1 основной нагрузкой передач является статическая нагрузка. Во всех случаях динамические нагрузки передач и элементов кинематической цепи механизма могут существенно дополнительно увеличиваться при возникновении в системе упругих механических колебаний.

Правильное определение нагрузок передач и других элементов кинематической цепи механизма имеет важное практическое значение. Нагрузки механического оборудования определяют его износ, причем наиболее неблагоприятно влияние нагрузок, содержащих знакопеременную составляющую. Поэтому ограничение максимальных нагрузок и уменьшение динамических колебательных нагрузок, обусловленных упругими связями, обеспечивают повышение надежности и долговечности механической части привода и механизма.


Динамические нагрузки механического оборудования в реальных установках в значительной мере возрастают из-за ударов, возникающих при выборе зазоров в передачах и сочленениях рабочего оборудования машин. С учетом кинематических зазоров расчетная двухмассовая схема механической части принимает вид, показанный на рис.1.28,а. В связи с наличием зазора Df3 зависимость М12=f(f1-f2) становится нелинейной и имеет вид, показанный на рис.1.28,б. Уравнения движения для этой системы на основании (1.40) запишутся при р=d/dt так:

Структурная схема механической части, соответствующая (1.71), представлена на рис.1.28,в. Рассматривая (1.71) и рис.1.28,в, можно установить, что при разомкнутом зазоре массы системы движутся независимо. Так как при этом М12=0, (1.71) при М=М1=const принимает вид:



Как следствие, к моменту соударения масс скорости w1 и w2 могут оказаться существенно разными. Так, при реактивном Мс2 на первом этапе пуска (М12=0) скорость w2 остается равной нулю, а скорость w1 быстро увеличивается, так как М1>Мс1.


К моменту окончания выбора зазоров она успевает нарасти до значения


где e1в.з=(М1-Мс1)J1 - ускорение при выборе зазоров.

Уравнение (1.74) записано для наиболее тяжелого случая выбора полного зазора, когда начальное значение Df на рис.1.28,б соответствует точке 1, а заканчивается выбор зазора в точке 2.

При реактивном характере момента Mc2 после выбора зазора скорость w2 будет оставаться равной нулю до тех пор, пока момент М12, возрастая, не превысит значения Мс2. За время нарастания момента М12 до Мс2 скорость w1 дополнительно увеличивается до значения w1нач, которое в конечном счете и определит динамическую нагрузку передач после трогания второй массы.

Из физических соображений можно заключить, что накопленная за время выбора зазора первой массой кинетическая энергия J1w12нач/2 должна при ударе реализоваться в дополнительных динамических нагрузках передач. Для количественного анализа получим зависимость М12=f(t) для третьего этапа процесса, когда |ф1 - ф2|>Dф3/2 + Mc2/c12.

На третьем этапе уравнения (1.71) можно представить в виде



Для получения дифференциального уравнения системы, решенного относительно М12, умножим первое уравнение на с12/J2 а второе на с12/J2 и произведем вычитание второго из первого. При этом с учетом третьего уравнения правая часть становится равной d2M12/dt2, и после преобразований полученное уравнение можно записать так:




где

С  учетом проведенного анализа предыдущих этапов выбора зазоров решение (1.76) следует искать при следующих начальных условиях:


Общее решение уравнения с учетом определяемого правой частью частного                решения и корней p1,2=±jW12 запишем в виде


Для определения коэффициентов А и В' используем начальные условия:

Следовательно,



где



После преобразований получим



где



В соответствии с (1.79) максимум нагрузки передач в рассматриваемом переходном процессе определяется соотношением



Анализируя (1.80), можно установить, что динамические нагрузки, обусловленные упругими колебаниями, существенно увеличивают нагрузки передач.


При отсутствии колебательной составляющей в (1.79) момент нагрузки передач в процессе пуска равен М12ср=J2eср+Мс2. За счет упругих колебаний в соответствии с (1.8(5) нагрузка возрастает, и ее превышение над средней нагрузкой называется динамическим коэффициентом:



При пуске с предварительно выбранными зазорами и Мс2=0 (Dw1нач=0) динамический коэффициент kдин=2, т. е. упругие колебания вдвое увеличивают рабочие нагрузки передач (рис.1.29). При наличии зазоров (Dw1нач¹0) максимум нагрузок возрастает и может достигать опасных для механической прочности передачзначений. Если подставить в (1.81) выражение eср, W12 и обозначить, как выше принято, JS/J1=g, коэффициент динамичности можно записать так:


Нетрудно видеть, что динамические коэффициенты, обусловленные упругими ударами, при выборе зазоров тем больше, чем больше момент инерции ротора двигателя и жестко с ним связанных элементов J1 и чем больше жесткость механической связи.

При Dw1нач¹0 упругость передач является фактором, снижающим динамические ударные нагрузки. В этом можно убедиться, подставив в (1.82) значение с12=¥, - ему соответствуют бесконечно большие динамические коэффициенты, т. е. разрушающие нагрузки передач. Однако и при реальных конечных значениях с12 удары при выборе зазоров могут создавать недопустимые нагрузки или существенно увеличивать износ механического оборудования. В этих случаях при проектировании электропривода предусматриваются законы управления, обеспечивающие повышение плавности выбора зазоров и снижение ударных нагрузок до допустимых значений путем ограничения достигаемой при выборе зазоров скорости Dw1нач.

Динамические колебательные процессы в среднем не влияют на длительность переходных процессов пуска, реверса и торможения электропривода. Однако они во многих случаях отрицательно сказываются на условиях выполнения технологических операций, особенно на точности работы установки. Практически всегда возникающие упругие колебания увеличивают динамические нагрузки механического оборудования и ускоряют его износ, т.е. являются одним из факторов, определяющих надежность, долговечность и производительность машин.

Динамический коэффициент является важной характеристикой условий работы механического оборудования, а его значения определяются, главным образом, динамическими свойствами электропривода. При проектировании и наладке электроприводов задача уменьшения динамического коэффициента до значений, близких единице, в связи с изложенным имеет важное практическое значение. Для многих механизмов она определяет выбор структуры, настроек и параметров электропривода и при успешном решении обеспечивает увеличение срока службы механического оборудования.

Динамические свойства асинхронного

Математическое описание динамических процессов преобразования энергии в §3.10 было получено в предположении, что двигатель получает питание от сети или от индивидуального преобразователя, обладающего свойствами источника напряжения, т. е. источника, напряжение которого при изменении тока нагрузки остается неизменным. Проведем с его помощью анализ динамических свойств асинхронного преобразователя, рассматривая его как объект управления. Как было показано, для реализации управления моментом и скоростью двигателя в широких пределах при благоприятных условиях необходимо изменять частоту подведенного напряжения, воздействуя на скорость поля и амплитуду напряжения, определяющую при данной частоте магнитный поток двигателя.

Анализ динамических процессов преобразования энергии в асинхронном двигателе представляет собой сложную задачу в связи с существенной нелинейностью уравнений (3.64) и (3.68), обусловленной наличием произведений переменных. Исследование динамических процессов при широких пределах изменения скорости целесообразно вести с применением вычислительной техники. Для этих целей удобную форму математического описания дает (3.68), если решить каждое уравнение относительно производной потокосцепления и записать:

Структурная схема электромеханического преобразования энергии в асинхронном двигателе при питании от источника напряжения представлена на рис.3.36. Рассматривая ее, можно видеть два управляющих воздействия: w0эл и  определяющих при данной скорости ротора w изменения электромагнитного момента двигателя М. Для обеспечения определенных условий протекания процессов между изменениями w0эл и  должна устанавливаться взаимосвязь, которую называют законами частотного управления. Аналитические оценки динамических свойств асинхронного электромеханического преобразователя могут быть получены для режимов малых отклонений скорости от статического значения путем разложения (3.86) в ряд Тэйлора. В частности, таким путем устанавливаются динамические свойства преобразователя в области рабочего участка механической характеристики s<sk в режимах, когда магнитный поток машины изменяется незначительно.

Здесь рассматривается динамический режим работы двигателя, имеющий место по истечении времени после подключения к источнику переменного напряжения, достаточного для затухания свободных составляющих, обусловленных переходным процессом включения. При этом предполагается, что отклонения скорости от значения, определяемого статической характеристикой, малы, а изменения токов не вызывают существенных изменений потокосцепления статора .

Для этих условий, положив d/dt=0, с помощью (3.64) можно определить потокосцепление статора по формуле



Следовательно, при питании от источника напряжения при неизменной частоте w0эл=const изменения Y1 вызываются только изменениями падения напряжения на активном сопротивлении статора R1 Если принять R1=0, то при неизменной частоте постоянство обеспечивает постоянство потокосцепления в широких пределах изменения скорости. При изменениях частоты f1 и R1=0 для поддержания постоянным  достаточно изменять напряжение пропорционально частоте:



Соотношение (3.88) определяет закон частотного управления U1/f1=const.

Пусть к обмоткам статора обобщенной машины приложена система синусоидальных напряжений, которым соответствует изображающий вектор  совпадающий по направлению с осью х, т. е. в осях х, у



Тогда в соответствии с (3.88)



Таким образом, для рассматриваемых условий процессы электромеханического преобразования в асинхронном двигателе описываются тремя последними уравнениями системы (3.86). Выполним вспомогательные преобразования:



Здесь индексом «н» обозначено, что индуктивные сопротивления х1н, x2н, хmн соответствуют номинальной частоте сети w0элном; учтено, что хmн>>х,н; sk определено из (3.77) при R1=0. С учетом полученных значений Y1x и Y1у и последнего соотношения три указанных уравнения системы (3.86) запишутся в виде




здесь

- электромагнитная постоянная времени;


абсолютное скольжение, равное отношению отклонения скорости двигателя w от скорости поля w0 при любой частоте f1 к скорости поля w0ном при частоте f1ном.

Положим d/dt=р и произведем преобразования алгебраизированных уравнений (3.89), имея в виду, что эти уравнения нелинейны и поэтому допустимы только такие их преобразования, при которых строго сохраняется предусмотренный исходными уравнениями порядок дифференцирования переменных.


С этой целью вначале из первого уравнения определим Y2:



Подставив (3.90) во второе уравнение системы (3.89) с соблюдением получающегося порядка дифференцирования переменных, получим



Подстановка (3.91) в третье уравнение системы (3.89) дает искомое выражение механической характеристики:



где



В последней записи критического момента Мк произведен переход от максимального напряжения U1max двухфазной модели двигателя к реальному действующему значению напряжения на фазе трехфазного двигателя U1. По формуле (2.37)



Кроме того, учтено, что хmн>>х1н и хmн>>х'2н. Нетрудно убедиться, что полученное значение Mk совпадает с определяемым по (3.78) при R1=0 и w0=w0 ном. Таким образом, полученное приближенное уравнение механической характеристики в качестве частного случая статического режима работы (р=0) дает уравнение статической механической характеристики (3.79) при R1»0. Однако оно выражено в функции абсолютного скольжения Sa:



поэтому не только приближенно описывает естественную характеристику двигателя (w0=w0ном), но и определяет искусственные механические характеристики двигателя, соответствующие различной частоте питающего напряжения f1 при изменении напряжения по закону U1/f1=const. Как следует из (3.93) и выражения Мк в (3.92), при R1=0 механические характеристики инвариантны относительно абсолютного скольжения sa и представляются зависимостями w=f(М), показанными для различных частот пунктирными кривыми на рис.3.37. Реально в (3.87) можно пренебрегать R1 только при частотах, близких к номинальной, при этом U1=U1ном>>I1R1. При снижении частоты и напряжения по закону U1/f1=const, как показывает (3.87), потокосцепление Y1 должно снижаться, стремясь к 0 при f1®0. Соответственно с учетом R1¹0 реальные механические характеристики при таком законе управления имеют снижающийся при малых частотах критический момент (см. сплошные кривые на рис.3.37). По этой причине в реальных системах используются более сложные законы частотного управления, рассматриваемые в гл. 7.



Уравнение механической характеристики ( 3 92) отражает влияние электромагнитной инерции на протекание динамических процессов электромеханического преобразования энергии при ограниченных по амплитуде колебаниях в окрестностях точек статической характеристики. Для анализа этого влияния осуществим линеаризацию этого уравнения. Вначале необходимо выполнить операции дифференцирования в последовательности, полученной при выводе (3.92)




После дифференцирования получим


Раскладываем полученное уравнение в ряд Тэйлора в окрестности точки М°, s°a, пренебрегая членами высшего порядка малости. После преобразований уравнение механической характеристики представляется в виде



Уравнение (3.94) позволяет анализировать модуль статической жесткости линеаризованной механической характеристики и влияние электромагнитной инерции при линеаризации в любой точке статической механической характеристики M°=f(s°). Наибольший интерес представляет линеаризованное уравнение механической характеристики для рабочего участка sa<sk. Такое уравнение получим с помощью (3.94), положив s0a=0,Dsа=sa-s0a=sa=(w0-w)/w0ном;DM=M-M0=M




Следовательно, в окрестности точки М°=0, s0a=0 электромеханический преобразователь представляется звеном первого порядка, так как его уравнение механической характеристики имеет вид

где b=2·Мк/w0ном·sк - модуль жесткости линеаризованной механической характеристики.

Структурная схема асинхронного электромеханического преобразователя, линеаризованного в пределах рабочего участка статической механической характеристики, представлена на рис 3.38.

Передаточная функция динамической жесткости в соответствии с этой схемой запишется так:



Сравнивая (3.95) и (3.96) с аналогичными формулами для двигателя постоянного тока с независимым возбуждением, можно заключить, что в пределах рабочего участка асинхронный двигатель имеет динамические свойства, аналогичные динамическим свойствам двигателя с независимым возбуждением.

Так как критическое скольжение двигателей лежит в пределах sk=0,05¸0,5, причем меньшие значения соответствуют мощным двигателям, электромагнитная постоянная двигателя Тэ при питании от источника напряжения невелика:



меньшие значения соответствуют двигателям малой мощности.

Динамические свойства электромеханического преобразователя с независимым возбуждением

Рассмотренные выше характеристики двигателя с независимым возбуждением получены в предположении, что двигатель питается от бесконечно мощной сети или от любого другого источника, обладающего свойствами источника напряжения с внутренним сопротивлением, равным нулю. Приступая к изучению динамических свойств, необходимо иметь в виду, что в регулируемом электроприводе возможно питание якорной цепи двигателя и от преобразователей, обладающих свойствами источника тока. Поэтому анализ динамических свойств электромеханического преобразрвателя с независимым возбуждением проведем для случаев питания как от источника напряжения, так и от источника тока.

Для анализа воспользуемся системой (3.6). Обозначив d/dt=р, запишем ее в виде

где Tв=Lв/Rв - электромагнитная постоянная времени обмотки возбуждения; Тя=LяS/Rя - электромагнитная постоянная времени цепи якоря; kф=Ф/iв - коэффициент, соответствующий линейной части кривой намагничивания двигателя.

Структурная схема электромеханического преобразования энергии, соответствующая (3.40), приведена на рис.3.11,а. На схеме представлены два возможных канала управления при питании от источника напряжения - канал управления полем двигателя, которому соответствует управляющее воздействие uв, и канал управления по цепи якоря с управляющим воздействием ия. Из схемы следует, что при отсутствии реакции якоря процессы в цепи возбуждения протекают независимо от процессов в якорной цепи, а процессы в якорной цепи зависят от изменений магнитного потока двигателя Ф.

Цепь возбуждения двигателя представляет собой апериодическое звено с постоянной времени Тъ, Индуктивность LB обмотки возбуждения может быть определена по формуле

где kнас=Iвном/Iвлин - коэффициент насыщения; Iвлин - ток возбуждения, создающий номинальный поток Фном при отсутствии насыщения магнитной цепи.

Значение индуктивности LB, определяемое данной формулой, соответствует линейной части кривой намагничивания. При работе в насыщенной части кривой намагничивания индуктивность и постоянная времени цепи возбуждения уменьшаются тем больше, чем выше насыщение:

Полученное в §3.6 математическое описание процессов электромеханического преобразования энергии в двигателе с последовательным возбуждением содержит произведения переменных, поэтому использовать его для анализа динамических свойств преобразователя можно лишь с помощью ЭВМ. Однако общие закономерности, основные динамические свойства электромеханического преобразователя с последовательным возбуждением могут быть выявлены аналитическим путем, если осуществить линеаризацию уравнений механической характеристики (3.50) в окрестности точки статического равновесия.

Так как линеаризация осуществляется в окрестности точки статического равновесия, кривую намагничивания следует аппроксимировать касательной в точке Iя0, Ф0, как показано на рис.3.22, при этом Ф=Ф0+k'ф(iя+iвт) и первые два уравнения системы (3.50) могут быть преобразованы к виду

Tв- постоянные времени соответственно эквивалентного контура вихревых токов (см. рис.3.15,б) и обмотки возбуждения. Вычтя почленно из первого уравнения второе, получим более удобный для решения вид системы (3.50):

Линеаризуем систему (3.57) путем разложения в ряд Тэйлора в окрестности точки статического равновесия, обозначим d/dt=р, получим

Решив систему (3.58) относительно Д/я и DМ, получим линеаризованные уравнения электромеханической и механической характеристик двигателя в виде

Уравнения (3.59) и (3.60) характеризуют основные динамические особенности преобразователя с последовательным возбуждением при условии ограничения отклонения переменных от точки статического равновесия узкими пределами. Сравнивая их, можно установить, что наличие контура вихревых токов определяет более значительные колебания тока, чем момента при тех же условиях. Это различие существенно усиливается, если не учитывать индуктивности рассеяния якорной цепи, положив Тя=0. При этом порядок числителя и порядок знаменателя (3.59) становятся одинаковыми, что свидетельствует о возможности изменения тока якоря скачком и существенно искажает действительный характер процессов.

При отсутствии добавочных резисторов у двигателей мощностью от 1 до нескольких тысяч киловатт постоянная времени цепи возбуждения лежит в пределах Tв=0,2¸5 с, причем с увеличением мощности двигателя она быстро возрастает.

Изменение потока вносит нелинейность в математическое описание процессов преобразования энергии даже при ненасыщенной магнитной цепи, поэтому при переменном магнитном потоке структура на рис 3.11,a используется для анализа динамических свойств электропривода постоянного тока с помощью ЭВМ. Для синтеза регулируемых электроприводов математическое описание электромеханического преобразователя линеаризуется путем разложения в ряд Тэйлора в окрестности точки статического равновесия.

При питании от источника напряжения двигатель с независимым возбуждением работает преимущественно при постоянном потоке: Ф=Фном=const, при этом уравнение механической характеристики двигателя в соответствии с (3.7) принимает вид



Этому уравнению соответствует структурная схема преобразователя, представленная на рис.3.11,б. Она свидетельствует о том, что при Ф=const электромеханический преобразователь представляет собой апериодическое звено с постоянной времени Тя. Индуктивность рассеяния якорной цепи двигателя может быть вычислена по приближенной формуле



где g=0,6 для некомпенсированных и g=0,25 для компенсированных двигателей.

Постоянная времени якорной цепи двигателей средней и большой мощности лежит в пределах Тя=0,02¸0,1 с, причем наибольшие значения соответствуют некомпенсированным либо тихоходным двигателям большой мощности.

Уравнение динамической механической характеристики устанавливает связь между механическими переменными в общем виде, справедливом для любых режимов работы электропривода. Форма конкретных динамических характеристик определяется совокупностью условий и связей, наложенных на движение электромеханической системы в данном процессе. Поэтому двигатель имеет бесчисленное множество динамических характеристик, соответствующих переходным процессам и зависящих от вида механической части, начальных условий, уровня и характера управляющих и возмущающих воздействий.


Эти характеристики несут информацию о свойствах динамической системы, состоящей из электромеханического преобразователя энергии и механической части, а для анализа электромеханических свойств самого преобразователя их непосредственно использовать нельзя.

В установившихся динамических режимах работы, обусловленных, например, наличием периодической составляющей нагрузки электропривода, динамическая механическая характеристика для каждого цикла установившихся колебаний одинакова, и форма ее зависит только от электромеханических свойств двигателя. Примем, что момент двигателя в установившемся динамическом режиме изменяется по закону М=Мср+DMmaxsin Wt.


Тогда (3.41) при p=d/dt однозначно определяет соответствующий закон изменения скорости:

где Y=arctg ТяW.

На рис.3.12 показаны характеристики w(t) и M(t) и соответствующая им динамическая характеристика - замкнутая кривая 1. Нетрудно видеть, что электромагнитная инерция якорной цепи вызывает значительные отклонения динамической характеристики 1 от статической 2. Уменьшение частоты вынужденных колебаний W. или соответствующее снижение постоянной времени Тя приводят к уменьшению этих отклонений (кривая 3), и в пределе при Тя®0 или Q®0 динамическая характеристика сливается со статической.

Эти рассуждения приводят к выводу о целесообразности использования для анализа динамических свойств двигателя частотного метода. Для этой цели с помощью структурной схемы рис.3.11,б определим передаточную функцию динамической жесткости механической характеристики (см. гл. 2)



Амплитудно-фазовую характеристику динамической жесткости получим подстановкой в (3.44) p=jW.:



Соответствующие (3.45) АЧХ и ФЧХ динамической жесткости



Амплитудно-фазовая характеристика динамической жесткости (3.45) представлена на рис.3.13,а, а на рис.3.13,б показаны соответствующие ей ЛАЧХ и Л ФЧХ. Рассматривая их, можно установить, что электромагнитная инерция приводит к уменьшению модуля динамической жесткости тем в большей степени, чем выше частота вынужденных колебаний Л.


Одновременно сдвиг по фазе между колебаниями скорости и момента изменяется от -180°, соответствующих статической жесткости (W=0), до -270° при Q®¥. Введение добавочных резисторов в цепь якоря уменьшает Tя, при этом, если в пределах возможных частот колебаний модуль динамической жесткости снижается незначительно, а фазовый сдвиг остается близким к 180°, можно без существенных погрешностей исследовать динамические процессы, пользуясь выражением статической механической характеристики.

Частотные характеристики динамической жесткости упрощают определение зависимости от времени одной из механических переменных по известной для установившегося колебательного режима другой. Если, как было принято выше, М=Мср+DMmax·sinW·t, зависимость w(t) определится соотношением



Зависимость М(t) по заданной функции w(t)=Dwmax·sinW·t определяется аналогичным путем:



Таким образом, суждение о жесткости естественной механической характеристики по статической зависимости М=f(w) и по модулю статической жесткости b дает правильные представления лишь для статических режимов или при достаточно плавных изменениях нагрузки. При изменениях нагрузки скачком, а также в установившихся колебательных режимах динамическая характеристика может существенно отклоняться от статической, и необходимо оценивать эти отклонения с помощью частотных характеристик динамической жесткости либо путем расчета соответствующего переходного процесса с учетом электромагнитной инерции двигателя.

Достоинством электромеханического преобразователя с независимым возбуждением при Ф=const является высокое быстродействие, определяемое относительно небольшой постоянной времени Тя. При этом следует иметь в виду, что проведенный анализ динамических свойств преобразователя полностью справедлив только для компенсированных двигателей. У некомпенсированных двигателей, как было отмечено выше, вследствие реакции якоря магнитный поток при изменениях тока якоря не остается постоянным, а может изменяться на 10-20 % в сторону уменьшения от Ф0.


Изменения основного потока машины происходят с постоянной времени цепи возбуждения Tв, намного большей, чем Тя. Соответственно инерционность преобразователя при проявлениях реакции якоря возрастает и расхождения между статическими и динамическими характеристиками проявляются при меньших частотах.

При питании якоря двигателя от источника тока iя=Iя1=const при любых изменениях ЭДС двигателя. Система (3.40) при этом приводится к следующему уравнению механической характеристики:



Рис 3.14 Статическая 1 и динамическая 2 характеристики двигателя П62

Этому уравнению соответствует структура электромеханического преобразователя, представленная на рис.3 11,в. Сравнивая рис.3.11,б и в, можно установить, что в режиме питания якоря от источника тока двигатель с независимым возбуждением утрачивает рассмотренные выше электромеханические свойства. Отсутствие зависимости тока якоря от скорости исключает проявление электромеханической связи, и статическая механическая характеристика двигателя М=f(w) при ub=const обладает жесткостью, равной нулю.

Как объект управления электромеханический преобразователь при этом представляет собой апериодическое звено с большой постоянной времени Tв, управляющим воздействием является напряжение, приложенное к обмотке возбуждения uя. В соответствии с рис.3.11,в электромеханический преобразователь при Iя=const является источником момента М=const, значения которого можно регулировать путем воздействия на инерционный канал возбуждения двигателя.




Поэтому во всех случаях, когда ставится задача оценки характера изменения тока и его значения в том или ином динамическом режиме, следует пользоваться уравнением (3.59), не прибегая к дополнительным упрощениям.



Структурная схема линеаризованного электромеханического преобразователя с последовательным возбуждением, соответствующая (3.60), представлена на рис.3.23. С помощью этой схемы определим передаточную функцию динамической жесткости механической характеристики:



Уравнение (3.61) свидетельствует о том, что динамическая жесткость в данном случае существенно зависит от положения точки статического равновесия на механической характеристике двигателя. При этом следует иметь в виду, что каждой точке статической характеристики соответствуют не только различные значения Ф°, Iя°, w0, но также и различные значения таких параметров, как TвS и k'ф. При уменьшении момента двигателя по сравнению с номинальным (М°<Мном) коэффициент k'ф возрастает и при уменьшении потока до значений, соответствующих линейной части кривой намагничивания, становится равным коэффициенту k'фmах=k'ф [см. рис.3.16 и формулы (3.53) и (3.54)]. При дальнейшем уменьшении момента и потока kф остается постоянным, соответственно максимально и постоянно значение TвS. В области перегрузок (М°>Мном) магнитная цепь двигателя насыщается, соответственно k'ф и TвS принимают достаточно малые значения.

Если учесть, что Тя и TВТ при I°я<Iном намного меньше, чем TBS и их произведение в (3.61) можно приближенно принять равным нулю, то для приближенных оценок получаем удобную формулу:



где- модуль статической жесткости;

- эквивалентная электромагнитная постоянная якорной цепи двигателя.

Формула (3.62) аналогична по форме формуле динамической жесткости двигателя с независимым возбуждением (3.44), но по существу отличается непостоянством модуля и эквивалентной электромагнитной постоянной в различных точках статической характеристики при I°я<Iном. Если магнитная цепь двигателя ненасыщенна, т. е. kф=k'ф=const, то k'фI°я=Ф°, и модуль статической жесткости определяется соотношением





из которого следует, что с уменьшением нагрузки статическая жесткость механической характеристики уменьшается весьма быстро как из-за уменьшения потока Ф°, так и из-за возрастания скорости w°. Модуль динамической жесткости при этом дополнительно снижается за счет электромагнитной инерции, характеризуемой постоянной времени Тэ так же, как и у двигателя с независимым возбуждением. При сопоставлении необходимо иметь в виду, что сумма TвS+Тя при ненасыщенной машине намного превосходит значение Тя для двигателя с независимым возбуждением, но включение обмотки возбуждения в силовую цепь приводит к тому, что Tэ зависит от скорости w0 и существенно снижается при увеличении скорости. В области насыщения при I°я>Iном k'ф»0 и ТВS - стремится к значению, соответствующему индуктивности рассеяния обмотки возбуждения, при этом b=k2Ф2/RЯS и Тэ=Тя=LЯS, где LяS - суммарная индуктивность рассеяния якорной цепи. Таким образом, в области перегрузок динамические свойства двигателя с последовательным возбуждением практически совпадают с рассмотренными выше свойствами двигателя с независимым возбуждением.

Линеаризованные характеристики двигателя с последовательным возбуждением (3.59) и (3.60) могут быть использованы для анализа установившихся колебательных режимов электромеханических систем с двигателем последовательного возбуждения, а также для проверки устойчивости и качества замкнутых систем регулирования с таким двигателем при малых отклонениях от положения статического равновесия.

Динамические свойства электропривода

При изучении свойств механической части электропривода было установлено, что во многих практических случаях влияние упругих колебаний на движение первой массы пренебрежимо мало. Имея в виду сочетания параметров механической части, при которых это условие выполняется, принимаем в (4.5) с12=¥, ф1=f2=ф, w1=w2=w. В результате получаем

Системе уравнений (4.11) соответствует структурная схема электропривода, представленная на рис.4.7. Эта схема заслуживает детального анализа, так как отражает основные свойства большого числа конкретных электромеханических систем при с12=¥. Наиболее полно она соответствует электроприводу постоянного тока с компенсированным двигателем независимого возбуждения. В пределах рабочего участка механической характеристики она удовлетворительно описывает динамику асинхронного электропривода как при питании от источника напряжения, так и при питании от источника тока. При линеаризации механической характеристики двигателя с последовательным возбуждением данная схема позволяет анализировать свойства таких электроприводов в области малых отклонений от выбранной точки статической характеристики. В последнем случае область соответствия (4.11) объекту расширяется при возрастании насыщения магнитной цепи.

Таким образом, рассмотрение свойств электромеханической системы, описываемой (4.11), дает представления о динамических особенностях большинства промышленных разомкнутых систем электропривода, при этом отдельного рассмотрения требуют лишь свойства синхронного электропривода в связи с отличием (4.10) от (4.11).

Для анализа свойств электропривода с линейной механической характеристикой как объекта автоматического управления получим передаточную функцию системы по управляющему воздействию. В соответствии с рис.4.7

где Тм=JS/b - электромеханическая постоянная времени. Передаточная функция по возмущающему воздействию - моменту статической нагрузки Мс - имеет вид

Характеристическое уравнение системы

Корни характеристического уравнения

где m=ТM/ТЭ - отношение постоянных времени электропривода.

Значение m является важным показателем динамических свойств электропривода, непосредственно определяющим колебательность разомкнутой электромеханической системы при жестких механических связях. Если m>4, то



Соответственно передаточная функция (4.12) может быть при таких параметрах преобразована к виду



где T1=1/a1; Т2=1/a2.

Следовательно, при m>4 рассматриваемый электропривод для анализа может быть представлен в виде последовательного соединения двух инерционных звеньев с постоянными времени T1 и Т2 Частотные характеристики электропривода при таком сочетании параметров имеют вид, показанный на рис.4.8,a. Реакцию электропривода на скачок управляющего воздействия при нулевых начальных условиях и Мс=0 характеризуют соответствующие (4.15) переходная функция



и импульсная (весовая) функция



 Соответствующие (4.16) и (4.17) зависимости представлены на рис.4.8,б. Зависимость h(t) дает представление о законе изменения скорости электропривода w(t) при приложении к якорю двигателя постоянного тока скачка напряжения Uя или изменении частоты тока статора асинхронного двигателя f1 скачком. Из уравнения движения при М=0 следует, что весовая функция h'(t) здесь характеризует в определенном масштабе изменения электромагнитного момента двигателя M(t). Максимум момента Mmax ~ h'max возрастает при увеличении скачка управляющего воздействия, поэтому при использовании (4.16) и (4.17) скачок uя или f1 должен быть ограничен значением, при котором Мmах остается в пределах, допустимых по перегрузочной способности двигателя или по условиям линеаризации механической характеристики.

При m=4 характеристическое уравнение системы имеет два равных отрицательных корня: р12=-a=-1/2Тэ. В этом случае передаточная функция (4.12) преобразуется к виду



где T=1/а.

Электропривод при таком сочетании параметров обладает свойствами, аналогичными рассмотренным для m>4. В этом можно убедиться, сравнивая приведенные на рис.4.9 частотные и переходные характеристики, соответствующие (4.18), с такими же зависимостями на рис.4.8.


Графики переходной h(t) и весовой h'(t) функций построены на рис.4.9,б по выражениям



При сочетаниях параметров, которым соответствуют значения m<4, характеристическое уравнение имеет комплексно-сопряженные корни



и электропривод представляет собой колебательное звено с коэффициентом затухания x<1, уменьшающимся по мере уменьшения т. Учитывая обозначения коэффициентов передаточной функции колебательного звена, принятые в теории управления, можно записать



С помощью (4.19) установим связь между параметрами электропривода и обобщенного колебательного звена:



Значениям m<4 соответствуют коэффициенты затухания x<1.

Частотные характеристики колебательного звена при    m=0,5;2;4 (x=0,35;0,71;1) представлены на рис.4.10,а,б. Они показывают, что при уменьшении m колебательность электропривода возрастает и при m<2 (x<0,71) в ЛАЧХ проявляется резонансный пик, быстро возрастающий с уменьшением m. Переходная функция электропривода при m<4 выражается соотношением



Импульсная функция:



На рис.4.10,б представлен ряд зависимостей h(t*), где t*=t/Tэ, соответствующих тем же значениям m, что и на рис.4.10,а. Рассматривая (4.14) и (4.21), можно установить, что общее время затухания колебаний зависит только от Тэ Так как Тэ=TM/m при данной постоянной Tм, затухание и частота колебаний определяются соотношением постоянных m. Только от m зависит и показатель колебательности - логарифмический декремент колебаний:


При m=2 и l=6,28 колебания затухают практически за один период, а скорость электропривода достигает установившегося значения с небольшим превышением его в переходном процессе, составляющим около 5% установившегося значения. При m<2 затухание колебаний ухудшается, и в переходном процессе максимальные значения скорости все в большей мере превышают установившееся значение. При данном m общее время переходного процесса увеличивается пропорционально увеличению ТM. Представленные на рис.4.8-4.10 ЛФЧХ Y(W) свидетельствуют о том, что при одинаковом максимальном угле сдвига колебаний по фазе Ymax=-p с уменьшением m изменения фазы в области частоты недемпфированного электромеханического резонанса Wэм=1/T1=1/ÖТэТм становятся все более быстрыми.



Сравнивая (4.12) и (4.13), можно убедиться, что при колебаниях нагрузки электромагнитная инерция определяет при прочих равных условиях более высокие амплитуды колебаний скорости в области резонанса в связи с наличием в числителе (4.13) передаточной функции форсирующего звена с постоянной времени Тэ.

Таким образом, электропривод с линейной механической характеристикой вследствие электромагнитной инерции представляет собой при жестких механических связях колебательное звено, показатели колебательности которого l и x зависят только от соотношения постоянных времени m=ТМ/ТЭ, а быстродействие определяется электромагнитной постоянной времени Тэ или при данном m - электромеханической постоянной времени ТM.

При работе на естественной характеристике значения Тэ лежат в пределах Тэ=0,01¸0,1с, причем для асинхронных двигателей Тэ при питании от источника напряжения меньше, чем для двигателей постоянного тока той же мощности. Электромеханическая постоянная Тм изменяется в более широких пределах, и ее удобно выразить через расчетную величину - электромеханическую постоянную времени собственно двигателя - и отношение моментов инерции электропривода JS и якоря двигателя Jдв:



Для двигателей мощностью выше 10 кВт ориентировочно Т=0,01¸0,1 с, причем обычно постоянная времени TМ.ДВ соизмерима или близка Тэ. Поэтому для электроприводов с небольшим моментом инерции механизма наиболее вероятные значения m заключены в пределах 0,5<m<2, а для электроприводов со значительной инерцией механизма m>2. Из изложенного следует, что в этих пределах резонансное усиление колебаний невелико и электропривод представляет собой колебательное звено с высоким коэффициентом демпфирования x>0,4.

Это обстоятельство при рассмотрении электропривода с линейной механической характеристикой как объекта автоматического регулирования позволяет прибегать к упрощенному представлению передаточной функции (4.12) в виде



т. е. заменять колебательное звено двумя апериодическими с постоянной Т1=ÖTэTM.


Асимптотическая ЛАЧХ, соответствующая (4.24), при W<1/ Т1 имеет вид горизонтальной прямой, совпадающей с осью абсцисс, а при W>l/T1, представляет собой прямую с наклоном -40 дБ/дек (штриховая линия на рис.4.10,а). Сравнивая эту зависимость с реальными ЛАЧХ колебательного звена при различных значениях x, можно установить, что при x>0,4 расхождения незначительны. Погрешность в сторону занижения амплитуды при x>0,4 не превышает 3 дБ, что обычно допустимо.

Для многих электроприводов малой мощности m>4, при этом можно пренебречь электромагнитной инерцией, положив в (4.11)



Структурная схема, соответствующая (4.25), приведена на рис.4.11,a. Ее нетрудно преобразовать к виду рис.4.11,б, который свидетельствует о том, что при этих параметрах электропривод с линейной механической характеристикой приближенно представляет собой инерционное звено с постоянной времени ТM. Частотные характеристики электропривода, соответствующие такому представлению, показаны на рис.4.11,в, а переходная и весовая функции, определяемые соотношениями



построены на рис.4.11,г. С помощью этого рисунка можно пояснить физический смысл электромеханической постоянной времени. Электромеханическая постоянная Тм представляет собой время, за которое электропривод достиг бы установившейся скорости, двигаясь равномерно ускоренно под действием постоянного динамического момента, равного начальному значению:



Сравнивая кривые, приведенные на рис.4.11, с аналогичными кривыми на рис.4.8, которые соответствуют m>4 при учете электромагнитной инерции, можно сделать следующие выводы. При анализе переходных процессов в разомкнутой системе электропривода при m>4, как правило, можно без большой погрешности пренебрегать влиянием электромагнитной инерции и принимать Тэ»0. При синтезе замкнутых систем регулирования координат электромеханической системы малую постоянную Тэ при m>4 следует учитывать во избежание ошибок, вносимых неучетом потери запаса по фазе на частоте среза контура регулирования, обусловленной электромагнитной инерцией электромеханического преобразователя.

 

Динамика электропривода с синхронным двигателем

Анализируя структурную схему на рис.4.4, можно установить, что при работе в синхронном режиме переходные процессы синхронного электропривода могут быть вызваны изменениями управляющих воздействий и возмущениями в механической части. Управляющими воздействиями являются напряжения на обмотках статора u1 частота f1 и пропорциональная ей угловая скорость поля w0, напряжение uв, приложенное к обмотке возбуждения. Возмущающими воздействиями в механической части являются моменты нагрузки Мс1 и Мс2, изменения которых вызываются технологическими причинами.

При питании двигателя от сети его пуск осуществляется в асинхронном режиме с помощью предусмотренной для этой цели на роторе короткозамкнутой пусковой (демпферной) обмотки. В этом режиме электропривод ускоряется до подсинхронной скорости wвх, при которой обмотка возбуждения включается на постоянное напряжение UB и происходит процесс втягивания двигателя в синхронизм. Переходные процессы, протекающие при вхождении двигателя в синхронизм, имеют важное практическое значение, и их особенности необходимо в дальнейшем проанализировать.

Напряжение U1max частота f1 при питании от сети могут изменяться лишь в связи с колебаниями напряжения и частоты сети, обусловленными изменениями ее нагрузки. Эти колебания ограничены действующими нормами, поэтому невелики и здесь могут не учитываться.

Анализ переходных процессов, возникающих при изменениях напряжения возбуждения обмотки ротора UB, представляет интерес в тех случаях, когда предусматривается автоматическое регулирование тока возбуждения для регулирования cos ф двигателя.

Основными возмущениями при питании от сети следует считать возможные изменения нагрузки электропривода. При ударном характере нагрузки, в процессах приложения и снятия нагрузки и, как было отмечено, в процессах втягивания в синхронизм динамические свойства синхронного электропривода проявляются достаточно полно, и на их рассмотрении здесь необходимо сосредоточить основное внимание.

В §3.15 было отмечено, что электромагнитная связь возбужденного ротора с полем статора аналогична упругой механической связи.
Влияние этой связи на динамику синхронного электропривода можно проанализировать при представлении механической части жестким приведенным звеном с помощью структурной схемы на рис.4.6, полученной при с12=¥ и линеаризации угловой характеристики двигателя. Эта схема при отсутствии у двигателя демпферной обмотки (b=0) показана на рис.4.37. Из рисунка видно, что при жестких механических связях синхронный электропривод без демпферной обмотки неработоспособен. Действительно, два интегрирующих звена, охваченных жесткой отрицательной обратной связью, как известно из теории автоматического управления, образуют недемпфированную колебательную систему с передаточной функцией

и частотой свободных колебаний 

Демпферная обмотка создает асинхронный момент, который обеспечивает затухание колебаний в системе. В соответствии с рис.4.6 при этом



где Tм=JS/b - электромеханическая постоянная времени.



Передаточная функция электропривода по возмущению Мс может быть также определена по структурной схеме рис.4.6 и представлена в виде



В ряде случаев представляет интерес передаточная функция синхронного электропривода, в которой выходной переменной является угол q=f0-f, или, что то же, синхронная составляющая момента двигателя Mсин»сэмq. Эту передаточную функцию получаем из (4.109), учитывая, что при w0=0, w=-Dw и q есть интеграл от Dw по времени:



Следовательно, функция (4.109) может быть представлена в виде



Соответствующая АФХ



Амплитудно-частотная характеристика



Фазо-частотная характеристика



Если известно, что момент нагрузки электропривода изменяется по закону Мс=Мс.max·sinWt, с помощью (4.112) и (4.113) можно определить зависимость угла 0 от времени в виде



где



Рассматривая полученные зависимости, можно установить, что они соответствуют колебательному звену с коэффициентом затухания, определяемым электромеханической постоянной Тм. Следовательно, при данном JS колебательность определяется модулем жесткости асинхронной механической характеристики b. Чем больше модуль жесткости, тем меньше при колебаниях нагрузки Мc амплитуда колебаний синхронной составляющей момента, тем меньше резонансное усиление колебаний при частоте, близкой частоте свободных колебаний Wэм.



Если сравнить передаточную функцию (4.31) упругой электромеханической системы, соответствующую J2=¥, g=¥ и Тэ=0, с передаточной функцией синхронного электропривода (4.110), можно убедиться, что их характеристические уравнения полностью совпадают. Это означает, что электропривод с синхронным двигателем эквивалентен асинхронному электроприводу с упругой механической связью при бесконечно большой массе механизма Роль упругой механической связи при этом выполняют силы электромагнитного взаимодействия между полями ротора и статора.

Структурная схема рис.4.6 и соответствующие ей передаточные функции синхронного электропривода при принятых допущениях могут быть использованы для анализа переходных процессов при приложении и снятии нагрузки. Дифференциальное уравнение системы относительно скорости двигателя w можно записать с помощью (4.108):



При питании от сети w0=const, dw0/dt=0 Уравнение, (4.115) при этом имеет вид



Корни характеристического уравнения



Если Wэм>1/2TM, корни являются комплексно-сопряженными:



Следовательно, решение (4.115) необходимо искать в виде



Значения А и В могут быть определены с помощью начальных условий: при t=0 (w)0=wнaч, (dw/dt)0=(Мнач-МС)/JS, причем









Откуда



Подставив А и В в (4.118), получим решение уравнения (4.116) в виде



Для получения уравнения системы относительно момента двигателя М определим по структурной схеме рис.4.6 передаточную функцию:



Откуда



При изменениях момента скачком при t>0, Мс=const. Соответственно для рассматриваемых процессов уравнение имеет вид



Решение (4.121) будем искать в виде



Значения С и D определяются по начальным условиям аналогично выполненному ранее расчету. С помощью уравнения механической характеристики найдем производную момента:



При t=0, М0=Мнач, а производная момента (dM/dt)0 вычисляется с помощью (4.122):





Определив с помощью начальных условий С и D получим решение M(t) в виде



Полученные решения (4 120) и (4.124) свидетельствуют о том, что при изменениях нагрузки скачком скорость синхронного электропривода совершает затухающие колебания относительно скорости поля, а его момент колеблется относительно момента Мс, постепенно затухая с коэффициентом затухания а.


Максимум момента и динамическое падение скорости при этом возрастают при увеличении скачка нагрузки и при увеличении начального отклонения скорости w от w0. Эти же показатели при прочих равных условиях уменьшаются при увеличении коэффициента затухания a.

Как следует из (4.117), коэффициент затухания возрастает при увеличении жесткости асинхронной механической характеристики b, т.е. при уменьшении Тм. При ТM<1/2WЭM демпфирование обеспечивает апериодический характер процессов. Однако практически эффект демпфирования ухудшается влиянием электромагнитной инерции на асинхронную составляющую момента Мас, которая при выводе уравнений не была учтена (Tэ=0).

Уравнение (4.124) получено при линеаризации угловой характеристики двигателя, поэтому оно даст удовлетворительные оценки показателей переходного процесса только при М£М=lМном.

Наличие демпферной обмотки позволяет осуществлять пуск синхронного двигателя путем прямого включения его на напряжение сети. Пусковые характеристики показаны на рис.4.38. Характеристика 1 соответствует относительно небольшому сопротивлению демпферной обмотки, при этом критическое скольжение мало, что увеличивает жесткость рабочего участка механической характеристики и уменьшает пусковой момент Мп. Характеристика 2 соответствует повышенному сопротивлению этой обмотки, поэтому имеет сниженную жесткость рабочего участка, но больший пусковой момент Мп.

С точки зрения условий асинхронного пуска двигателя до подсинхронной скорости wвх, которой соответствует скольжение sвх, предпочтительна характеристика 2, особенно при значительной нагрузке на валу.

При достижении двигателем подсинхронной скорости wвх в цепь обмотки возбуждения подается постоянный ток, магнитный поток возрастает до номинального значения и наступает второй этап пуска - втягивание двигателя в синхронизм. Строгий анализ этого режима осложняется протекающими электромагнитными процессами. В первом приближении для оценки условий втягивания в синхронизм можно воспользоваться (4.120) и (4.124).


Для удобства анализа этого процесса решение системы уравнений синхронного электропривода при допущениях, соответствующих (4.110), получают относительно угла q, изменения которого при втягивании в синхронизм заслуживают особого внимания. В отклонениях от точки статического равновесия это решение имеет следующий вид:





При одной и той же нагрузке статическая характеристика 2 на рис.4.38 обеспечивает меньшую начальную скорость при втягивании в синхронизм. Соответственно при этом sвх2>sвх1 и амплитуда колебаний угла Dqmax в (4.125) получается большей. Реальной угловой характеристике синхронного двигателя при больших Dq соответствуют уменьшающиеся значения сэм. Как следствие, с ростом sbx условия втягивания в синхронизм ухудшаются и при больших sвx синхронизация может оказаться невозможной.

Таким образом, более благоприятные условия втягивания в синхронизм обеспечиваются жесткой механической характеристикой 1. Практически пусковая обмотка рассчитывается так, чтобы обеспечивались удовлетворительные условия пуска при заданном максимальном значении нагрузки Мс mах, а значения входного скольжения лежали в допустимых пределах: sbx=0,03¸0,05.

Естественные характеристики двигателя с независимым возбуждением

Электрический двигатель проектируется и изготавливается для определенного расчетного режима, называемого номинальным режимом работы (см. гл. 5). Этот режим реализуется в естественной схеме включения, которая для двигателя с независимым возбуждением приведена на рис.3.2. Она соответствует отсутствию добавочных сопротивлений в якорной цепи и номинальным значениям напряжения Uя=UHOM и потока Ф=Фном. Электромеханическая и механическая статические характеристики двигателя, соответствующие этим условиям работы, называются естественными характеристиками:

где w0ном- скорость идеального холостого хода при работе на естественной характеристике; bе- модуль статической жесткости естественной механической характеристики; с - коэффициент ЭДС и момента при номинальном потоке.

Естественная механическая характеристика двигателя дает основные представления об электромеханических свойствах двигателя. Она определяет его рабочую - номинальную - скорость и показывает, как изменяется скорость электропривода при изменениях нагрузки в статических режимах работы. Чем выше модуль жесткости естественной характеристики bе, тем более стабильна скорость электропривода при широких пределах изменения его нагрузки, и напротив, при малой жесткости механической характеристики изменения рабочей скорости механизма при изменениях нагрузки могут быть значительными.

Другой оценкой стабильности рабочей скорости электропривода при различных нагрузках является статизм механической характеристики двигателя. Количественной оценкой статизма может служить номинальный перепад скорости Dwном=w0ном-wном, соответствующий изменению момента двигателя от М=0 до М=Мном. Его значения связаны с модулем жесткости механической характеристики соотношением, определяемым из (3.18):

Таким образом, статизм механической характеристики обратно пропорционален модулю ее жесткости. Для получения необходимых представлений о реальных жесткостях естественных механических характеристик различных двигателей с независимым возбуждением необходимо записать уравнение механической характеристики в относительных единицах.

В качестве базисных величин обычно принимаются Uном, Iном, Фном, Rя.ном=Uном/Iном; w0ном; Mном при этом уравнения (3.9) и (3.10) в относительных единицах имеют следующий вид:



здесь



Уравнения естественных электромеханической и механической характеристик в относительных единицах могут быть получены с помощью (3.25) и (3.26) при Ф*=1 и w0*=1:



Так как при Ф=Фном М*=Iя*, уравнения (3.27) и (3.28) идентичны и естественные электромеханическая и механическая характеристики в относительных единицах совпадают (рис.3.3,a). Номинальный перепад скорости на естественной характеристике Dwном* в относительных единицах, как это следует из (3.27), равен относительному сопротивлению якоря RЯ*. Относительный ток короткого замыкания обратно пропорционален Rя*:



Собственное сопротивление якорной цепи Rя<<Rном, поэтому ток короткого замыкания на естественной характеристике у двигателей средней и большой мощности превышает номинальный в 10-20 раз. Он значительно превосходит ток Iя.доп, допустимый по условиям коммутации, и лежит далеко за пределами показанного на рис.3.3,а рабочего участка естественной механической характеристики. Перегрузочная способность двигателей с независимым возбуждением нормального исполнения обычно лежит в пределах l=Мдоп/Мном=2¸2,5 и для компенсированных двигателей совпадает с кратностью допустимой по условиям коммутации перегрузки по току.

Благодаря малости относительного сопротивления якорной цепи номинальный перепад скорости на естественной характеристике для двигателей средней и большой мощности составляет несколько процентов скорости идеального холостого хода и уменьшается с возрастанием мощности двигателя. Соответствен но жесткость механической характеристики при этом возрастает обратно пропорционально сопротивлению:



Относительный перепад скорости Dwном, для двигателей большой мощности весьма мал и лежит в пределах Dwном=0,015¸0,03. Двигатели небольшой мощности имеют на порядок больший статизм естественной механической характеристики, причем форма их характеристик отличается от показанной на рис.3.3,а.



Уравнение (3.22) с достаточной точностью описывает механические характеристики двигателей с независимым возбуждением, имеющих компенсационную обмотку. Все двигатели малой мощности и значительная часть двигателей средней мощности не имеют компенсационной обмотки, поэтому для них уравнение (3.22) описывает механические характеристики приближенно.

Для некомпенсированных двигателей форма механической характеристики отклоняется от показанной на рис.3.3,а в связи с действием продольной составляющей поперечной реакции якоря. Эта составляющая при UB=const вызывает уменьшение потока двигателя Ф по мере роста тока якоря в нелинейной зависимости. Рассматривая уравнение механической характеристики (3.10), можно установить, что такое влияние реакции якоря подобно нелинейной положительной обратной связи по току, так как при увеличении тока якоря увеличивается расчетное значение .скорости идеального холостого хода. При малых токах якоря действие реакции якоря проявляется слабо и kФ=const. В этой зоне, соответствующей Iя<Iном, реальная естественная характеристика двигателя имеет примерно постоянную жесткость:



где Ф0 - поток двигателя в режиме идеального холостого хода.

В номинальном режиме работы (IЯ=Iном) реакция якоря может заметно снижать поток двигателя, поэтому обычно Фном<Ф0, а жесткость механической характеристики не определяется (3.16), так как существенное влияние на изменения скорости при изменениях тока и момента двигателя оказывают изменения w0. Номинальный перепад скорости при этом меньше, чем у компенсированной машины того же типа, в связи с тем, что Фном<Ф0:



Соотношение (3.31) можно преобразовать к виду



где Dw'ном=IНОМ·Rя/k·Ф0 - номинальный перепад скорости компенсированной машины.

Если в (3.32) ввести номинальный перепад потока Ф'ном, то она примет вид



Формула (3.33) показывает, что реакция якоря уменьшает номинальный перепад скорости в тем большей степени, чем относительно меньше сопротивление якорной цепи.

В области перегрузок (IЯ>Iном) размагничивающее действие реакции якоря возрастает и увеличение первого члена в уравнении (3.9) может превышать возрастание его второго члена, обусловленного падением напряжения на Rя.Следовательно, в механической характеристике некомпенсированных двигателей могут быть участки, где bст=dM/dw>0.


При дальнейшем увеличении тока якоря и момента двигателя определяющим вновь становится возрастание падения напряжения в цепи якоря и жесткость механической характеристики становится отрицательной.

Проведенный анализ позволяет представить форму реальной механической естественной характеристики некомпенсированных двигателей с независимым возбуждением, как показано на рис.3 3,б (кривая 7). Здесь же показана характеристика 2 компенсированной машины, у которой Фном=Ф0. Кроме того, характеристика 3 показывает, как располагается относительно реальной естественной характеристики характеристика, рассчитанная по (3.23) при реальном потоке Фном<Ф0, вычисленном по паспортным данным двигателя (см. пример 3.1).

Рассматривая рис.3.3,б, можно установить, что продольная составляющая поперечной реакции якоря неблагоприятно сказывается на форме естественной механической характеристики двигателя, искажая ее форму. Кроме того, реакция якоря неблагоприятно сказывается на перегрузочной способности двигателя. При токе, соответствующем допустимой по условиям коммутации перегрузке, поток двигателя вследствие наличия реакции якоря снижается на 10-20 %. Соответственно пропорциональность между током и моментом нарушается и перегрузочная способность некомпенсированных двигателей при прочих равных условиях ниже, чем у компенсированных.

Изменение потока главных полюсов машины из-за реакции якоря неблагоприятно сказывается и на динамических свойствах электропривода, поэтому в некомпенсированных двигателях мощностью до 100 кВт применяют так называемые стабилизирующие обмотки, размещаемые на главных полюсах машин. Эти обмотки включаются в цепь якоря последовательно и создают небольшую положительную МДС, компенсирующую действие реакции якоря. Такие двигатели предназначаются для нереверсивного режима работы, так как при изменении направления вращения ток якоря в двигательном режиме имеет противоположное направление и стабилизирующая обмотка действует против МДС обмотки главных полюсов, усугубляя влияние реакции якоря.

Проведенный анализ естественных характеристик двигателя с независимым возбуждением свидетельствует о том, что его использование в разомкнутых системах электропривода, т. е. при питании от сети постоянного тока, целесообразно в тех случаях, когда для приводимого в движение механизма требуется работа при стабильной скорости, мало меняющейся при изменениях нагрузки. В замкнутых системах регулирования координат электропривода имеется возможность формировать требуемые для механизма механические характеристики, при этом естественные характеристики двигателя определяют исходные свойства электропривода, которые системой управления корректируются в требуемом направлении.

Фазные преобразования переменных

Из изложенного следует, что рассмотренное линейное преобразование переменных обобщенной машины имеет вполне определенный физический смысл. Переменные токи обмоток фаз обобщенной машины сдвинуты на электрический угол, равный 90°. На такой же пространственный угол смещены геометрические оси обмоток фаз, поэтому результирующая МДС вращается относительно создающих ее обмоток со скоростью, пропорциональной частоте тока.

Мгновенное положение вектора результирующей МДС определяется геометрической суммой векторов МДС соответствующих обмоток, поэтому токи этих обмоток можно рассматривать как проекции вектора результирующей МДС на их оси. Как следует из рассмотрения рис.2.3, один и тот же вектор результирующей МДС может быть создан парами как неподвижных, так и вращающихся обмоток. Формулы преобразования токов и устанавливают взаимосвязь между проекциями результирующего вектора тока на соответствующие оси а, b, d, q или u, v.

Математическое описание механических характеристик получено для двухфазной модели машины. Реальные двигатели переменного тока чаще всего имеют трехфазную обмотку статора, поэтому возникает необходимость преобразования переменных трехфазной машины к переменным двухфазной модели и наоборот. Основой для такого преобразования может служить рассмотренный физический смысл координатных преобразований. Действительно, один и тот же результирующий вектор МДС может быть создан как двухфазной, так и трехфазной обмоткой, поэтому для получения формул двухфазно-трехфазных преобразований можно использовать тот же принцип, что и для получения формул координатных преобразований.

Итак, возникает задача преобразования реальных переменных x1a, x1b, х1с статора трехфазной машины к ортогональной системе координат a, b, т. е. к реальным переменным статора эквивалентной двухфазной машины. Решение этой задачи существенно осложняется в связи с необходимостью перехода от объекта с тремя фазами к обобщенной модели с двумя фазами, так как разница в числе фаз затрудняет выполнение условия инвариантности мощности.
Учитывая это, представим реальные переменные трехфазной машины в виде векторов и будем полагать, что преобразованные переменные в осях a, b не равны, а пропорциональны сумме проекций реальных переменных x1a, х1b, х1с на оси a, b. На основании построения, показанного на рис.2.6,а, можно записать

где kc - согласующий коэффициент пропорциональности, выбор которого должен осуществляться из условия инвариантности мощности.

Рассмотрим наиболее распространенный в практике случай, когда переменные трехфазной машины подчиняются условию



С учетом (2.33) уравнения (2.32) преобразуются к виду



Переменные x2d, x2q для роторной цепи машины также определяются (2.33) и (2.34) при соответствующей замене индексов.

Формулы обратного преобразования можно получить аналогично с помощью рис.2.6,б:




При выполнении условия (2.33) третье уравнение системы (2.35) может быть получено с помощью первых двух, так как x1c=-(x1a+ x1b). Для определения согласующего коэффициента kс, обеспечивающего выполнение условия инвариантности мощности при преобразовании переменных, выразим с помощью (2.35) суммарную мгновенную мощность, потребляемую обмотками статора трехфазной машины через переменные эквивалентной двухфазной машины:

Следовательно, для выполнения условия инвариантности мощности согласующий коэффициент должен иметь значение kc =, при этом



В более общем случае х1а+x1b+x1c¹0, и тогда приходится считаться с наличием переменных нулевой последовательности x0. В соответствии с [12] формулы прямого и обратного преобразования для этих условий имеют вид



Практически необходимость использования формул преобразования (2.36) и (2.37) возникает при строгом анализе несимметричных режимов работы симметричной трехфазной машины. При этом следует иметь в виду, что токи нулевой последовательности не влияют на момент, развиваемый двигателем, поэтому в большинстве случаев влияние переменных нулевой последовательности на динамику электромеханических систем может не учитываться.

При необходимости установления количественной связи между переменными трехфазной машины и ее двухфазной модели в статических режимах достаточно воспользоваться одним уравнением из систем (2.34) или (2.36).Для этого необходимо изображающий вектор переменной  совместить с осью a модели и с совпадающей с ней осью а реальной машины, при этом х1b=0 и связь между амплитудами переменных определяется первыми уравнениями систем (2.34) и (2.35):



где x1max(2ф) и x1max(3ф) – амплитуды соответственно двухфазной модели и трехфазной реальной машины.

Искусственные статические характеристики и режимы работы двигателя с независимым возбуждением

Для управления работой двигателя производятся необходимые изменения параметров и воздействий, определяющих его механические и электромеханические характеристики. В соответствии с (3.9) и (3.10) такими параметрами и воздействиями являются суммарное сопротивление якорной цепи RяS, магнитный поток машины Ф, приложенное к якорной цепи напряжение Uя. Характеристики, соответствующие измененным параметрам двигателя или специальным схемам его включения, принято называть искусственными характеристиками двигателя.

Искусственные характеристики, полученные путем введения добавочных резисторов в цепь якоря, называются реостатными характеристиками двигателя. Схема включения резистора для получения реостатных характеристик представлена на рис.3.5,я. При этом суммарное сопротивлениеякорной цепи увеличивается:

Соответственно ограничивается ток короткого замыкания

и уменьшается модуль жесткости статической механической характеристики

Скорость идеального холостого хода остается неизменной w0=w0.ном, а между током и моментом, если не учитывать реакцию якоря, сохраняется пропорциональность М=с·Iя, поэтому механические и электромеханические реостатные характеристики двигателя отличаются друг от друга только масштабом по оси абсцисс.

Семейство механических и электромеханических характеристик двигателя для ряда значений Rдоб представлено на рис.3.5,б. Введение резисторов в цепь якоря двигателя является простейшим средством ограничения тока при различных переходных процессах и используется для этой цели во всех случаях при питании двигателя от сети.

Как следует из (3.33), увеличение сопротивления якорной цепи RяS влечет за собой относительное снижение влияния реакции якоря на характеристики двигателя, поэтому при расчете реостатных характеристик влиянием реакции якоря можно пренебречь.

Изменение потока двигателя Ф в связи с насыщением его магнитной цепи в номинальном режиме практически возможно в сторону уменьшения потока - ослабления поля двигателя. Уменьшение потока вызывает увеличение скорости идеального холостого хода w0 и уменьшение момента короткого замыкания Мкз, а ток короткого замыкания при этом не претерпевает изменений.
Соответственно модуль статической жесткости механической характеристики уменьшается пропорционально квадрату потока, о чем свидетельствует (3.16). Изложенным объясняется форма статических характеристик двигателя при различных потоках, построенных на рис.3.6 с помощью формул (3.9) и (3.10). При рассмотрении этих характеристик следует иметь в виду, что рабочий участок характеристик двигателя ограничивается его перегрузочной способностью и, как показано на рис.3.6 утолщенными отрезками характеристик, лежит вблизи скорости идеального холостого хода. Нетрудно видеть, что ослабление поля в пределах рабочих нагрузок приводит к увеличению скорости двигателя.

Изменение напряжения, подведенного к якорю двигателя при номинальном потоке, является в регулируемом электроприводе постоянного тока основным управляющим воздействием. Как правило, изменение напряжения Uя возможно только в сторону уменьшения по сравнению с номинальным, причем для мощных двигателей это ограничение является жестким, так как допустимое по условиям работы коллектора повышение напряжения невелико. Ряд двигателей краново-металлургических серий рассчитан на возможную работу с напряжением Uя=2Uном, однако это является исключением из общего правила. Как следует из (3.10), при изменении Uя пропорционально изменяется скорость идеального холостого хода двигателя, а жесткость механических характеристик при любом уровне напряжения одинакова, поэтому механические характеристики при Uя=var имеют вид параллельных прямых, показанных на рис.3.7. В отличие от ослабления поля изменение напряжения на якоре позволяет не только изменять скорость, но и ограничивать ток короткого замыкания. Плавное повышение напряжения на якоре от 0 до Uном обеспечивает наиболее благоприятные условия пуска двигателя.

В представленном на рис.3.7 семействе характеристик определенным своеобразием отличается характеристика, соответствующая Uя=0. Так как энергия к якорной цепи от внешнего источника не подводится, эта характеристика проходит через начало координат и полностью располагается только во втором и четвертом (тормозных) квадрантах.


При наличии активной нагрузки, приложенной к валу, якорь двигателя приводится во вращение за счет подведенной со стороны механизма механической мощности. Под действием возрастающей ЭДС двигателя в якорной цепи, замкнутой через источник питания накоротко, начинает протекать ток и машина развивает тормозной момент, противодействующий движущему моменту активной нагрузки. Это режим динамического торможения, в котором двигатель работает генератором на сопротивление якорной цепи. В общем случае, когда сеть имеет нерегулируемое напряжение, т. е. Uс=Uном=const, для осуществления режима динамического торможения двигатель должен быть отключен от сети и его якорь замкнут на внешний резистор Rдоб (рис.3.8,а). Уравнения статических характеристик двигателя при динамическом торможении можно получить, положив в (3.9) и (3.10) Uя=0:





Рис.3.8. Схема включения (а) и хар-ки двигателя с независимым возбуждением (б, в)

Увеличение сопротивления якорной цепи RяS из-за введения добавочных сопротивлений Rдоб уменьшает жесткость механических характеристик в режиме динамического торможения так же, как и в двигательном режиме. Аналогично изменяется модуль жесткости механических характеристик динамического торможения и при ослаблении поля двигателя. Механические характеристики, соответствующие различным Rдоб, представлены на рис.3.8,б, а при ослаблении поля - на рис.3.8,в. Электромеханические характеристики при введении сопротивлений отличаются от механических только масштабом по оси абсцисс, как это и отмечено на рис.3.8,б. При переменном потоке коэффициент пропорциональности между током и моментом для различных характеристик неодинаков, поэтому на рис.3.8,в представлены только механические характеристики, а подобные им по форме электромеханические не показаны.

Используем полученные представления о статических характеристиках двигателя с независимым возбуждением для анализа его режимов работы с энергетической точки зрения. Нэ рис.3.9,а- д изображен ряд возможных схем включения электропривода подъемного механизма с двигателем независимого возбуждения и показаны механические характеристики, позволяющие проанализировать соответствующие режимы работы двигателя.



Для осуществления режима подъема номинального груза Гр со скоростью wпгр двигатель включается по схеме, показанной на рис.3.9,a Установившийся режим подъема определяется на рис.3.9,д естественной механической характеристикой двигателя 1, причем принято, что статический момент при подъеме груза Мсп равен номинальному моменту двигателя Мном. При этом двигатель работает в двигательном режиме, и для якорной цепи уравнение электрического равновесия можно записать так:



где Iном=Iс п- статический ток при подъеме груза


Умножив левую и правую части уравнения на Iном, получим уравнение баланса мощностей в этом режиме:

здесь Uном·Iном - электрическая мощность, потребляемая из сети, часть которой теряется в якорной цепи в виде теплоты (I2ном·RяS) а основная часть преобразуется в механическую электромагнитную мощность



Для спуска груза со скоростью vс.гр, близкой к скорости vn.гр , двигатель включается по той же схеме, но к его якорю подводится напряжение противоположного знака Uя=-Uном. Естественная характеристика 2, соответствующая этой полярности, и статический момент при спуске груза Мсс определяют на рис.3.9,д рабочую точку Мсс; wсс, которая соответствует генераторному режиму работы Действительно, при этом активный момент Мсс вращает двигатель со скоростью wс с по значению большей, чем скорость идеального холостого хода w0ном. Следовательно, ЭДС двигателя больше, чем напряжение сети, и с учетом знаков скорости, напряжения и ЭДС баланс мощностей в этом режиме можно представить так:



Уравнение (3.37) показывает, что механическая мощность, вырабатываемая опускающимся грузом, в основном отдается в сеть, а частично теряется в виде теплоты на сопротивлениях якорной цепи. Это генераторный режим работы параллельно с сетью или режим рекуперативного торможения двигателя

Для получения пониженной скорости спуска груза двигатель может быть включен по схеме, приведенной на рис.3.9,в. Сравнивая ее со схемой рис.3.9,а, можно убедиться, что она соответствует включению двигателя для работы в направлении подъема груза, но в цепь якоря вводится большое добавочное сопротивление Rдоб , ,при котором момент короткого замыкания (пусковой момент Мп) меньше, чем активный момент нагрузки при спуске груза Мсс.


Как показано на рис.3.9, д такой выбор добавочного сопротивления (характеристика 3) обеспечивает тормозной спуск груза со скоростью w'сс при этом активный движущий момент нагрузки принуждает якорь вращаться в сторону, противоположную заданной приложенным
напряжением, и уравнение баланса мощностей записывается так:

В соответствии с (3.38) потребляемая из сети мощность UномIясс и вырабатываемая вследствие опускания груза механическая мощность Мссw''cc=E''сc·Iясс в этом режиме превращаются в тепловые потери в якорной цепи двигателя. Это генераторный режим работы двигателя последовательно с сетью, чаще называемый режимом торможения противовключением. Сравнивая (3.37) и (3.38), можно видеть, что торможение противовключением является неэкономичным режимом, в котором поступающая с вала механическая мощность не отдается в сеть, а вместе с потребляемой из сети электрической мощностью преобразуется в теплоту, выделяющуюся на сопротивлениях якорной цепи.

По сравнению с режимом противовключения более экономичным тормозным режимом является динамическое торможение двигателя. Этот режим работы рассматриваемой подъемной установки обеспечивается включением двигателя по схеме рис.3.9,г. Выбором добавочного сопротивления Rдоб2 можно обеспечить спуск груза с требуемой по условиям технологии скоростью wс определяемой механической характеристикой 4 на рис.3.9,д. Баланс мощностей для режима динамического торможения (Uя=0) имеет вид



Здесь механическая мощность преобразуется в электрическую (Мссw"с=E''сс·Iясс) и выделяется в виде теплоты на сопротивлениях якорной цепи. Более высокая экономичность режима динамического торможения по отношению к режиму торможения противовключением наглядно устанавливается сравнением (3.38) и (3.39). Сравнивая (3.37) с (3.39), можно убедиться в большей экономичности режима рекуперативного торможения, в котором значительная часть механической мощности преобразуется в электрическую мощность, отдаваемую в электрическую сеть, и лишь часть выделяется в виде теплоты в сопротивлениях якорной цепи.

Электромеханическая связь электропривода и ее характеристики

Уравнения электрического равновесия (2.8) и уравнение электромагнитного момента (2.10) представляют собой математическое описание динамических процессов преобразования энергии во вращающихся электрических машинах, записанное в общем виде и выраженное через действительные переменные двухфазной модели. Вместе (2.8) и (2.10) образуют систему из пяти уравнений, устанавливающую взаимосвязь между процессами в механической и электрической частях электромеханической системы. Проявления этой взаимосвязи в теории электропривода называются электромеханической связью.

Для разъяснения сути этого понятия воспользуемся уравнениями электрического равновесия (2.8). В соответствии с (2.6) и (2.7) индуктивности Li,j зависят от электрического угла поворота ротора фэл, а следовательно, и от времени t. Поэтому, выполнив дифференцирование в (2.8), можно эти уравнения представить в виде

где w=df/dt - угловая скорость ротора машины.

Первый член каждого уравнения (2.12) представляет собой падение напряжения на активном сопротивлении цепи данной обмотки, второй - результирующую ЭДС самоиндукции и взаимной индукции еLi вызванную изменениями токов в обмотках, а третий член отражает взаимодействие механической и электрической частей электропривода, так как представляет собой результирующую ЭДС ei наведенную в обмотке в результате механического движения ротора машины:

Наличие в (2.12) ЭДС ei, зависящих от скорости ротора двигателя, приводит к тому, что изменения скорости, вызванные процессами в механической части, вызывают изменения токов ii потребляемых обмотками машины. Рассмотренное явление представляет собой электромеханическую связь в системе электропривода, благодаря которой при питании двигателя от источника напряжения существует зависимость токов силовой цепи электропривода от его скорости. Так как токи ii благодаря электромеханической связи зависят от скорости ротора машины, то и ее электромагнитный момент, определяемый (2.10), также является функцией скорости.

Качественными и количественными характеристиками электромеханической связи, широко используемыми в теории электропривода, являются электромеханические и механические характеристики.
Электромеханическими характеристиками называются характеристики ii=f(w) или w=f(ii), соответствующие статическим или конкретным динамическим режимам работы электропривода. Аналогичные характеристики М=f(w) и w=f(М), связывающие в этих режимах электромагнитный момент и скорость электропривода, называются механическими характеристиками.

Уравнения электрического равновесия (2.12) выражают математическую связь между функциями ii(t) и w(t) в динамических процессах электромеханического преобразования энергии. Следовательно, эти уравнения представляют собой обобщенное математическое описание электромеханических характеристик двигателя во всех режимах работы. Поэтому в дальнейшем они называются уравнениями электромеханической характеристики двигателя.

Система уравнений, составленная из уравнений электромеханической характеристики (2.12) и электромагнитного момента (2.10), устанавливает математическую связь между функциями M(t) и w(t) во всех режимах работы, т. е. является обобщенным математическим описанием механических характеристик двигателя. В дальнейшем эти уравнения называются уравнениями механической характеристики.

Таким образом, уравнения (2.12) вместе с (2.10) образуют систему уравнений механической характеристики двигателя:

Все множество электромеханических и механических характеристик, определяемых (2.12) и (2.14), в зависимости от режимов работы электропривода разделяется на динамические и статические характеристики. Всем динамическим процессам соответствуют динамические электромеханические ii=f(w) и механические М=f(w) характеристики, а статическим - статические. Уравнения статических характеристик получаются из общих уравнений динамики (2.12) и (2.14) путем подстановки в них условий, соответствующих статическим режимам работы.

Электромеханическая связь объединяет механическую часть электропривода и электромеханический преобразователь в единую электромеханическую систему. Действительно, благодаря наличию этой связи электромагнитный момент двигателя реагирует на процессы, протекающие в механической части, и в свою очередь оказывает влияние на эти процессы.Как следствие, электромеханическая связь определяет важные физические свойства разомкнутых и замкнутых электромеханических систем, и ее характеристики в теории электропривода являются эффективным инструментом для изучения этих свойств. Создание электроприводов, обладающих требуемыми качествами, как ниже будет показано, практически реализуется путем формирования требуемых статических и динамических механических характеристик электропривода.

Электромеханические переходные

Выполненный в §4.6 анализ динамических свойств обобщенной разомкнутой электромеханической системы с упругой механической связью, структура которой приведена на рис.4.5 и 4.14, позволяет при рассмотрении электромеханических переходных процессов сосредоточить внимание на характере переходных процессов электропривода при жестких механических связях, приняв с12=¥. В соответствующей этому условию структурной схеме электропривода с линейной механической характеристикой (см. рис.4.7) скорость идеального холостого хода w0 является обобщенным управляющим воздействием. Значения w0 для электропривода постоянного тока определяются приложенным к якорной цепи напряжением uя, а для асинхронного электропривода - частотой тока статора f1.

В широко применяемых электроприводах, получающих питание от сети, электромеханические переходные процессы протекают при неизменном напряжении uя или частоте f1 т.е. при w0=const. Переходные процессы электропривода при этом могут быть вызваны: а) включением двигателя, при этом w0 скачком изменяется от нуля до w0ном (пуск); б) изменением знака w0ном также скачком (торможение противовключением, реверс); в) отключением двигателя от сети и включением по схеме динамического торможения, при котором w0 скачком уменьшается от w0ном до нуля (динамическое торможение); г) изменением сопротивления якорной RяS или роторной R'2S цепи двигателя при Mс=const (изменение скорости электропривода); д) изменением нагрузки на валу двигателя (скачок нагрузки).

Так как переходные процессы пуска и торможения должны протекать при ограниченных значениях тока двигателя, то при w0=const в силовую цепь вводятся добавочные резисторы Rя доб для двигателей постоянного тока и R2доб для асинхронных двигателей), при этом влияние электромагнитной инерции снижается и при достаточно большом сопротивлении добавочного резистора можно приближенно при расчете переходных процессов принимать Тэ=0. Необходимость учета электромагнитной инерции (Tэ¹0) обычно возникает при расчете переходных процессов, когда добавочные резисторы отсутствуют и двигатель работает на естественной характеристике.

С учетом изложенного получим общее решение дифференциального уравнения системы при Тэ¹0 и ненулевых начальных условиях. Электромеханические переходные процессы в рассматриваемой системе описываются уравнением механической характеристики и уравнением движения электропривода при с12=¥:

Решив второе уравнение относительно момента М и подставив это выражение в первое, получим дифференциальное уравнение системы, решенное относительно скорости:


Аналогично получим дифференциальное уравнение системы, решенное относительно момента:


Анализ корней характеристических уравнений (4.43) и (4.44) выполнен в §4.4. Если m=ТМ/ТЭ< 4, то


при этом общее решение уравнения (4.43) следует искать в виде


Уравнения для определения коэффициентов А и В можно получить, подставив в (4.45) начальные условия  


Определив А и В и подставив их выражения в (4 45), получим решение дифференциального уравнения (4.43) в виде

При m<4 общее решение уравнения (4.44) следует искать в виде



Для нахождения коэффициентов С и D необходимо определить начальное значение производной момента (dM/dt)0, полагая (М)0=Мнач. В соответствии с первым уравнением системы (4.42) при (w)0=wнач



откуда



где Dwнач=w0-wнач. Полученные начальные условия при подстановке в (4.47) дают уравнения для определения С и D:




Решив эти уравнения относительно С и D и подставив решения в (4.47), получим

Если m>4, то p1=-a1 и p2=-a2. В этом случае общее решение уравнения (4.43) должно быть записано так:



Значения А' и В' определяются аналогично определению А и В в (4.45) при тех же начальных условиях. Определив А' и В' и подставив их в (4.50), получим



Таким же образом при m>4 получается общее решение (4.44):



Полученные решения (4.46), (4.49), (4.50а) и (4.51) позволяют рассчитывать все перечисленные выше переходные процессы при w0=const при любых начальных условиях и сочетаниях параметров, если m<4 и m>4. В трех редких случаях, когда m=4 и р1=p2=-a решения уравнений (4.43) и (4.45) следует искать в виде





и определять неопределенные коэффициенты А", В", С" и D" по тем же начальным условиям, что и рассмотренные ранее.

Используем полученные решения для анализа конкретных переходных процессов в разомкнутой системе электропривода с линейной механической характеристикой. Как уже отмечалось, учет влияния электромагнитной инерции требуется при работе электропривода на естественной механической характеристике. Для многих механизмов значительный интерес представляет оценка падения скорости электропривода, обусловленного ударным приложением нагрузки. Рассмотрим этот режим.

На рис.4.22,а представлена естественная механическая характеристика двигателя 1. Примем, что двигатель работает в статическом режиме, М=Мс.нач, w=wс.нач, причем m<4. В момент времени t=0 нагрузка скачком увеличивается от Мс.нач до Мс. Так как предшествующий режим был установившимся, в (4.46) и (4.49) Мнач=Мс.нач и wнач=wс.нач.

Если учесть, что при этом



уравнение (4.46) можно представить в виде



При записи уравнения (4.49) для рассматриваемого режима нужно учесть, что при Мнач=bDwнaч в соответствии с (4.48) (dM/dt)t=0=0:



Общий характер процесса при этом определяется отношением постоянных времени m и для m=1 иллюстрируется зависимостями w, М =f(t), приведенными на рис.4.22,б. Физические особенности процесса удобно проследить, сопоставляя естественную характеристику 1 с построенной с помощью графиков на рис.4.22,б динамической механической характеристикой для рассматриваемого процесса 2 (рис.4.22,а). При возрастании скачком момента нагрузки происходит процесс снижения скорости, вызывающий в свою очередь рост тока и момента двигателя. Однако вследствие наличия индуктивности рассеяния нарастание момента двигателя идет медленнее, а скорость снижается в большей степени, чем это определяется статической характеристикой 1. Поэтому при возрастании момента до М=Мс скорость w<wс, что влечет за собой дальнейший рост момента до Mmax. Колебания затухают, и после двух-трех их периодов достигается установившийся режим М=Mc, w=wс.



Максимальное динамическое падение скорости Dwmax при этом превышает статическое падение Dwс в тем большей степени, чем больше жесткость статической характеристики и чем больше Тэ. Таким образом, отклонения скорости от требуемого значения из-за электромагнитной инерции существенно увеличиваются, что для механизмов с ударной нагрузкой в ряде случаев по условиям технологии является неблагоприятным. Заметим, что вывод о влиянии электромагнитной инерции уже был получен при частотном анализе динамической жесткости механических характеристик электропривода. Увеличение модуля динамической жесткости в широком диапазоне частот влечет за собой уменьшение динамического перепада скорости при ударном приложении нагрузки. Если предшествующий режим не является установившимся, пользоваться для расчета уравнениями (4.52) и (4.53) недопустимо, так как для этого случая решения имеют вид (4.46) и (4.49).

Во всех случаях, когда электропривод работает на реостатных характеристиках (Rядоб¹0 или R2доб¹0), значения Тэ пренебрежимо малы и можно принимать Тэ=0. В §4.4 было показано, что при Тэ=0 электропривод с линейной механической характеристикой представляет собой апериодическое звено с постоянной времени Тм (рис.4.11,б). Уравнения переходного процесса для этих условий получим с помощью (4.51) и (4.52), положив в них a1=a=-1/Тм и a2=¥:



Графики переходного процесса, соответствующие (4.54) и (4.55), представлены на рис.4.23. Если продифференцировать уравнение (4.54), можно получить зависимость от времени ускорения электропривода



где енач=(wс-wнач)/Tм - начальное ускорение электропривода. Рассматривая рис.4.23,a и б, видим, что уменьшение ускорения по мере возрастания скорости, определяемое (4.56), объясняется непрерывным уменьшением динамического момента Mдин=M-Mс от начального значения Мдин.нач=Мнач-Мс до нуля по мере возрастания скорости от wнач до wс. Если бы динамический момент в переходном процессе оставался равным начальному Мдин.нач=const, скорость w изменялась бы по линейному закону, как показано на рис.4.23,б тонкой касательной к начальной точке кривой w(t).


При этом время переходного процесса, как отмечено в §4.4, было бы равно электромеханической постоянной времени электропривода ТM. Практически время переходного процесса tпп=(3¸4)TM, когда w=(0,95¸0,98)wуст.

 

Рис.4.24 Реостатный пуск электропривода с линейной механической характеристикой

Рассмотрим с помощью полученных уравнений процесс реостатного пуска электропривода с линейной механической характеристикой, предположив, что система управления электроприводом в процессе пуска обеспечивает автоматическое переключение ступеней пускового реостата таким образом, что начальное и конечное значения момента двигателя остаются неизменными (рис.4.24,а). В начальный момент пуска в силовую цепь введено полное сопротивление пускового реостата, которое ограничивает пусковой момент значением М1 (пусковая характеристика 1). При увеличении скорости до значения wкон, выводится первая ступень пускового реостата, момент вновь возрастает до М1 про должается пуск по характеристике 2 и т. д С учетом (4.54) и (4.55) движение электропривода на каждой ступени можно характеризовать соотношениями





где Тм=JS/bi; bi - модуль жесткости i-й пусковой механической характеристики.

Зависимости w(t) и M(t) для рассматриваемого процесса пуска приведены на рис.4.24,б. Время работы на каждой пусковой характеристике можно определить, подставив в (4.57) или (4.58) значения wконi или соответственно Мконi=М2 и решив полученные показательные уравнения относительно времени:





По мере увеличения скорости и перехода от ступени к ступени добавочное сопротивление Rя.доб или R2.доб уменьшается и модуль жесткости Р( увеличивается. Это приводит к постепенному уменьшению продолжительности работы на пусковых ступенях, как это видно из рис.4.24.

На переходный процесс реверса электропривода, как было установлено в §1.7, оказывает влияние характер статического момента. Если реверс осуществляется при активном моменте Мс==const, система электропривода остается линейной и зависимости w, М=f(t) описываются уравнениями (4.54) и (4.55) во всем диапазоне изменения скорости.


Механические характеристики, соответствующие рассматриваемому процессу, показаны на рис.4.25,а. Здесь прямая 1 является характеристикой, с которой электропривод работал в предшествующем режиме; если считать предшествующий режим установившимся, эта характеристика определяет начальную скорость при реверсе wнач, соответствующую моменту Мс. Для осуществления реверса на якоре двигателя постоянного тока скачком меняется полярность напряжения uя или на статоре асинхронного двигателя изменяется чередование фаз, а в силовую цепь двигателя для ограничения тока вводятся добавочные резисторы (характеристика 2)



Характер изменения скорости во времени определяется (4.54) при подстановке в это выражение значения установившейся скорости с противоположным знаком:



Зависимость момента от времени определяется (4.55) при



Графики w, М=f(t), соответствующие (4.61) и (4.62), представлены на рис.4.25,б сплошными кривыми 1 и 2. Нетрудно видеть, что при рассмотренном процессе реверса установившаяся скорость - wс значительно превышает скорость идеального холостого хода и что длительность процесса могла бы быть сокращена путем постепенного выведения ступеней реостата. Поэтому обычно используется лишь первая часть рассмотренного процесса - торможение противовключением до скорости w=0, а затем следует реостатный пуск до естественной характеристики, аналогичный рассмотренному выше. В случаях, когда торможение противовключением используется для останова электропривода, двигатель при скорости w=0 отключается от сети.

Реактивный момент нагрузки при переходе скорости через нуль изменяет знак (рис 4.25,a). Поэтому до w=0 процесс торможения протекает так же, как и при активном моменте, и изображается сплошными кривыми w(t) и M(t) на рис.4.25,б. При изменении направления вращения реактивный момент изменяет знак, и процесс пуска в этом направлении описывается уравнениями (4.54) и (4.55) при других значениях начальной и установившейся скорости (wнач=0; wс=-w'c), а также начального и установившегося момента (Мнач=-Мп; Мс=-Мс):







Зависимости w, M=f(t) для пуска в противоположную сторону представлены на рис.4.25,б штриховыми линиями 3 и 4. Заметим, что при переходе через нуль скорости динамический момент скачком изменяется от значения



до значения



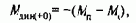
что влечет за собой соответствующее изменение ускорения электропривода. Этим объясняется излом в зависимостях w, М=f(t) при w=0, хорошо видный на рис.4.25,б (переход от сплошных к штриховым линиям 3 и 4).

В заключение рассмотрения переходных процессов при Тэ=0 остановимся на процессе динамического торможения. Для осуществления этого режима двигатель отключается от сети и включается по схеме динамического торможения (см.рис.3.8,а 3.44,а), причем в силовую цепь вводится резистор. Для двигателя постоянного тока этот резистор должен обеспечить ограничение тока допустимым по условиям коммутации значением, а для асинхронного двигателя выбирается из условия получения требуемого момента при переключении М1.

Соответствующие механические характеристики представлены на рис.4.26,а Модуль жесткости статической характеристики при динамическом торможении можно определить по отношению приращения момента к приращению скорости, например b=M1/wнач. Вычислив соответствующее значение ТM=JS/b и подставив в (4.54) установившееся значение скорости - wс, определяемое, как показано на рис.4.26,a активным моментом нагрузки Мс, получим выражения, совпадающие по форме с (4.61) и (4.62) Графики переходного процесса приведены на рис.4.26,б, причем при активном моменте нагрузки двигатель под действием нагрузки разгоняется в обратном направлении до скорости - wс, а при реактивном останавливается.

Заканчивая анализ процессов пуска и торможения в электроприводах, получающих питание от сети (w0=const), заметим, что все полученные зависимости w(t) и M(t) существенно отличаются от рассмотренных в §4.7 оптимальных по тем или иным критериям. Близкую к оптимальной по быстродействию кривую w(t) можно получить при реостатном пуске, если выбрать число пусковых ступеней достаточно большим.Повысить плавность нагружения упругой системы можно путем введения предварительных пусковых и тормозных ступеней с существенно меньшим начальным моментом, чем М1. Таким способом часто пользуются в различных подъемно-транспортных машинах в целях уменьшения рывков при выборе слабины канатов и ударов в передачах при выборе зазоров. Однако без применения автоматического регулирования момента или ускорения получить процессы, близкие к оптимальным, в большинстве случаев не удается.

 

Электромеханические свойства двигателей

3.1. Общие сведения

Наиболее широкое применение в электроприводе промышленных установок находят двигатели постоянного тока с независимым, смешанным и последовательным возбуждением, а также асинхронные и синхронные двигатели переменного тока.

Двигатели постоянного тока используются в электроприводе механизмов, требующих по технологическим условиям регулирования скорости. При этом двигатели со смешанным и последовательным возбуждением, как правило, применяются в разомкнутых системах электропривода. Двигатели с независимым возбуждением в настоящее время являются основой замкнутых систем регулируемого электропривода и наиболее широко используются в массовых тиристорных электроприводах постоянного тока.

Асинхронные короткозамкнутые и синхронные двигатели имеют основное применение в массовых нерегулируемых электроприводах. Благодаря конструктивной простоте и меньшей металлоемкости подавляющее число нерегулируемых электроприводов малой и средней мощности выполняется на базе асинхронных короткозамкнутых двигателей. В нерегулируемых электроприводах средней и особенно большой мощности применяются синхронные двигатели, которые рассчитываются на работу с опережающим cos ф и могут служить источником реактивной мощности для питающихся от той же сети асинхронных двигателей и тиристорных электроприводов постоянного тока. Асинхронные двигатели с фазным ротором применяются в электроприводах механизмов, требующих регулирования скорости, либо при необходимости ограничения пусковых токов, потребляемых из сети электроприводом. Проектирование, наладка и эксплуатация электроприводов требуют глубоких знаний свойств электрических машин с позиций их использования в электроприводе. Поэтому задачей данной главы является закрепление и развитие представлений об общих физических свойствах двигателей, полученных в курсе электрических машин, и изучение их особенностей и характеристик как объектов управления в системах электропривода. В соответствии со схемой рис.В.2 здесь изучаются свойства идеализированных электромеханических преобразователей, вырабатывающих электромагнитный момент М при скорости w, определяемой движением механической части и рассматриваемой как независимая механическая координата.
Влияние момента инерции ротора двигателя Jдв и момента механических потерь на валу DМ, входящих в соответствии с рис.В. 2 в механическую часть электропривода, на движение электропривода уже было рассмотрено в гл. 1.

В результате изучения материалов данной главы студенты должны знать и уметь использовать в практических целях математическое описание динамических процессов преобразования энергии в различных двигателях, их статические характеристики, оценки влияния различных параметров, структурные схемы и частотные характеристики электромеханических преобразователей различного типа.

Необходимо научиться правильно оценивать влияние электромагнитной инерции на процессы преобразования энергии, уметь определять границы, в которых для оценки динамических свойств двигателей можно пользоваться их статическими характеристиками. Следует обратить внимание на количественные оценки электромагнитной инерционности двигателей постоянного и переменного тока с учетом насыщения магнитной цепи машины. Сравнительные оценки быстродействия электромеханического преобразователя с независимым возбуждением по каналам управления якорной цепью и цепью возбуждения, а также асинхронного электромеханического преобразователя при питании от источников напряжения и тока имеют важное практическое значение.

Для облегчения понимания и усвоения материала перед изучением данной главы необходимо повторить ряд основополагающих вопросов из курса электрических машин. К их числу относятся устройство машин постоянного и переменного тока и назначение их основных элементов, статические механические характеристики, понятие реакции якоря и условий коммутации токов на коллекторе машины постоянного тока, представления о магнитном поле машины при холостом ходе и под нагрузкой и об основных его характеристиках. Полезно запомнить ряд основных соотношений, таких, как выражения ЭДС вращения и электромагнитного момента машины, схемы замещения и векторные диаграммы машин переменного тока, частотные характеристики апериодического звена, изученные в курсе теории автоматического управления.



Изучение свойств электромеханических преобразователей осуществляется на основе анализа статических и динамических механических характеристик, определяющих зависимость электромагнитного момента двигателя от напряжения или частоты, скорости ротора и параметров электрических цепей. Для правильного понимания режимов преобразования энергии необходимо использовать знания, полученные в главе «Механика электропривода». В частности, в соответствии с основным уравнением движения (1.42) в статических режимах работы при Мс=const электромагнитный момент машины равен моменту нагрузки электропривода М=Мс. Следовательно, в статических режимах работы механическую характеристику двигателя можно рассматривать как зависимость скорости электропривода от момента статической нагрузки его механической части. В динамических режимах М¹Мс, поэтому подобная интерпретация смысла механической характеристики недопустима.

В процессе изучения материалов данной главы необходимо научиться рассчитывать параметры двигателей и их статические характеристики, а также составлять структурные схемы электромеханических преобразователей. Эти навыки должны быть получены на практических занятиях и при выполнении курсовой работы. Необходимые рекомендации, расчетные соотношения и методы изложены в примерах.

Электромеханические свойства синхронных двигателей

Синхронные двигатели, как правило, исполняются с явнополюсным ротором, на котором размещается обмотка возбуждения. Питание обмотки возбуждения осуществляется через контактные кольца от источника постоянного напряжения, а трехфазная обмотка статора подключается к сети переменного тока, как показано на рис.3.46,a. Двухфазная модель такой машины представлена схемой на рис.3.46,б. Здесь обмотки фаз статора питаются симметричной двухфазной системой напряжений

Обмотка возбуждения размещена на оси d явнополюсного ротора и подключена к источнику постоянного напряжения ив. Уравнения электромеханической характеристики, записанные для реальных переменных в осях а, р, d, q, имеют вид

Особенностью рассматриваемого двигателя является синхронное вращение ротора с вращающимся полем статора. При работе в двигательном режиме ротор отстает от поля статора на угол qЭЛ=j0эл-jэл=w0эл·t-jэл, поэтому наиболее удобный для анализа вид уравнения механической характеристики имеют в осях d, q. Вначале преобразуем напряжения u1a, м1b к осям d, q с помощью формул прямого преобразования (2.15):

 

Подставив преобразованные выражения напряжений в (3.113) и дополнив эту систему уравнением электромагнитного момента, получим уравнения механической характеристики синхронного двигателя в осях d, q:

Схема синхронного двигателя в осях d, q представлена на рис.3.46,в. В соответствии с этой схемой записываем уравнения потокосцеплений, учитывая, что вследствие явнополюсности ротора

Уравнения (3.114) нелинейны в связи с наличием произведений переменных, поэтому для строгого анализа динамических режимов синхронного двигателя следует использовать цифровые или аналоговые вычислительные машины. Приближенное уравнение динамической механической характеристики может быть найдено с помощью угловой статической характеристики двигателя, для получения которой положим в (3.114) d/dt=0 и wэл=w0эл, пренебрежем активным сопротивлением статора R1»0, примем, что обмотка возбуждения получает питание от источника тока и во всех режимах iв=-Iв=const, при этом система (3.114) примет вид

Из первого и второго уравнений (3.116) определяются токи статора:



Подставляя выражения токов в третье уравнение (3.116) и учитывая, что L12dIB=Emах/w0эл, после преобразований получаем уравнение угловой характеристики двухфазного явнополюсного синхронного двигателя в виде



Произведем замену переменных двухфазной машины переменными трехфазной с помощью (2.37) и перейдем к эффективным значениям ЭДС и напряжения. В результате получим известное уравнение угловой характеристики трехфазного явнополюсного синхронного двигателя:



Уравнение (3.118) свидетельствует о том, что электромагнитный момент синхронного двигателя состоит из двух составляющих, первая из которых обусловлена взаимодействием вращающегося поля статора с полем возбужденного ротора, а вторая представляет собой реактивный момент, обусловленный явнополюсным исполнением ротора. Вследствие явнополюсности энергия магнитного поля максимальна при любом из двух возможных соосных с полем статора положений ротора, что и определяет зависимость реактивного момента от двойного угла qэл.

Примерный вид угловой характеристики М=f(qэл) показан на рис.3.47,а. Рассматривая ее, можно убедиться, что увеличение угла qэл вызывает рост электромагнитного момента вначале в зависимости, близкой к линейной. При qЭЛ> 45° темп нарастания момента быстро снижается, и после достижения максимума Мmах дальнейшее возрастание угла q влечет за собой уменьшение момента двигателя. Без учета явнополюсности ротора максимум момента наступает при qЭЛ=90°.

В номинальном режиме работы, когда двигатель развивает номинальный электромагнитный момент Мном, угол qэл обычно составляет qЭЛном=20¸30°. Этим обстоятельством определяется перегрузочная способность синхронного двигателя, которая лежит в пределах l=Мтaх/Мном=2¸3. Рассмотрение рис.3.47,а,б позволяет заключить, что реактивный момент увеличивает крутизну рабочего участка угловой характеристики и несколько повышает перегрузочную способность двигателя.

Перегрузочная способность синхронного двигателя менее чувствительна к понижению напряжения сети, чем у асинхронного двигателя, что относится к числу его важных достоинств.


Этот вывод следует непосредственно из (3.118), если учесть, что реактивный синхронный момент, зависящий от квадрата напряжения, мало влияет на перегрузочную способность, а основная составляющая момента зависит от напряжения U1 линейно, так как ЭДС машины Е определяется током возбуждения Iв.

Механизм образования синхронного момента виден на рис.3.46,в. На этом рисунке обозначены все токи, определяющие направление вектора потокосцепления статора  связанного с осью вращающегося магнитного поля машины. Вектор  определяется геометрической суммой потокосцеплений обмотки статора по оси d



и по оси q Y1q=L1qI1q. В соответствии с (3.117) на рисунке приведены зависимости токов I1d и I1q от угла qэл Рассматривая рисунок, можно установить, что при идеальном холостом ходе I1q=0 и вектор  совпадает с осью ротора d. Под нагрузкой ось ротора d и составляющая вектора потокосцепления Y1d, которая в основном определяется током возбуждения, отстают от оси вращающегося магнитного поля, определяемой положением вектора  на угол qЭЛ. Между постоянным магнитом, которым является возбужденный ротор, и вращающимся магнитным полем возникают силы взаимодействия. При малых углах qЭЛ эти силы при увеличении qЭЛ возрастают по закону, близкому к линейному. Нетрудно видеть, что рассмотренное электромагнитное взаимодействие вполне подобно механической упругой связи между полем ротора и результирующим полем машины. Поэтому по главным динамическим свойствам синхронный двигатель подобен упругим механическим системам.

Рабочий участок угловой характеристики М=f(qэл) можно с достаточной для многих задач инженерной практики точностью заменить линейной зависимостью М=kqэл, проходящей через точку номинального режима:



где сэм - коэффициент жесткости упругой электромагнитной связи двигателя.

Дифференцируя (3.119), получаем приближенное уравнение динамической характеристики:



Как было установлено в гл. 1, момент упругого взаимодействия М12 в двухмассовой линейной упругой системе



Дифференцирование этой зависимости дает уравнение, совпадающее по форме с (3.120), что еще раз подтверждает аналогию между электромагнитными взаимодействиями в синхронном двигателе и механическими в механической пружине.


Этим определяется повышенная склонность синхронного двигателя к колебаниям, для устранения (или снижения) которой реальные синхронные двигатели снабжаются демпферной (пусковой) короткозамкнутой обмоткой. Эта обмотка выполняется в виде беличьей клетки на полюсах ротора и при возникновении колебаний скорости ротора, т. е. скольжения, создает асинхронный момент. Пренебрегая влиянием электромагнитной инерции на асинхронный момент, результирующий момент синхронной машины в динамических процессах можно приближенно представить в виде суммы синхронного Мсин и асинхронного моментов Мас:



где

С учетом (3.120) уравнение механической характеристики синхронного двигателя в операторной форме примет окончательный вид



Структурная схема электромеханического преобразования энергии, соответствующая (3.122), представлена на рис.3.48,а. При р=0 из (3.122) получаем уравнение статической механической характеристики w=w0=const. Следовательно, в статическом виде изменения нагрузки на валу двигателя не приводят к изменениям скорости, так как модуль статической жесткости равен бесконечности. Это справедливо лишь в пределах перегрузочной способности двигателя, определяемой угловой характеристикой на рис.3.47,д. При возрастании нагрузки до значений, превышающих Мmax=lМНОМ, двигатель выпадает из синхронизма. Статическая механическая характеристика синхронного двигателя соответственно имеет вид, показанный на рис.3.47,б (прямая 1).

В динамических режимах механическая характеристика синхронного двигателя, как следует из (3.122), не является абсолютно жесткой. В установившемся динамическом режиме вынужденных колебаний изменениям момента с амплитудой DМmах и соответствующим изменениям угла qэл по (3.122) соответствуют определенные амплитуды Dwmах колебаний скорости и динамическая механическая характеристика имеет вид эллипса (рис 3.47,б, кривая 2). Передаточная функция динамической жесткости определяется по рис.3.48,а:



Соответственно АФХ, АЧХ и ФЧХ динамической жесткости определяются соотношениями





Логарифмические частотные характеристики динамической жесткости представлены на рис.3.48,б. Низкочастотная асимптота ЛАЧХ динамической жесткости имеет наклон -20 дБ/дек, поэтому модуль жесткости характеристики синхронного двигателя при возрастании частоты быстро убывает, стремясь к значению, определяемому жесткостью рабочего участка асинхронной характеристики M=f(w), а фазовый сдвиг y(W) изменяется от –3p/2 до -p.

Частотные характеристики динамической жесткости свидетельствуют о том, что соответствующая статическим режимам абсолютно жесткая характеристика синхронного двигателя для анализа динамических процессов неприменима. Динамические механические характеристики, соответствующие даже сравнительно медленным изменениям момента двигателя, могут существенно отличаться от статических.

Важным достоинством синхронного двигателя является возможность регулирования реактивной мощности путем воздействия на ток возбуждения Iв. Выражение для тока 11d (3.117) свидетельствует о том, что при прочих равных условиях этот ток и его знак определяются током возбуждения Iв, которому пропорциональна при принятых для обобщенной машины допущениях ЭДС Еmax. Ток I1q не зависит от тока возбуждения, поэтому влияние возбуждения двигателя на условия преобразования энергии можно проанализировать с помощью векторных диаграмм, соответствующих системе (3.116) при qЭЛ=const, представленных на рис.3.49.

При относительно небольшом токе возбуждения Emax<Umax·cos qЭЛ и ток I1d направлен в отрицательную сторону оси d (рис.3.49, a), при этом ток статора  отстает от приложенного напряжения на угол f1 и из сети потребляется реактивная мощность. Это потребление тем больше, чем меньше ток возбуждения. Увеличивая ток возбуждения, можно изменить направление тока I1d и установить такое его значение, при котором вектор тока статора  совпадает по направлению с напряжением сети (рис.3.49,б), при этом двигатель потребляет из сети (или отдает в сеть) только активную мощность, работая с cos f1=1. Дальнейшее увеличение тока возбуждения и ЭДС двигателя Е приводит к работе двигателя с опережающим cos ф1 и отдаче реактивной мощности в сеть (рис.3.49,в).

Из сравнения векторных диаграмм на рис.3.49 можно заключить, что при qЭЛ=const увеличение тока возбуждения и ЭДС E вызывает увеличение активной составляющей тока  рост активной мощности, а следовательно, и момента двигателя. При неизменном моменте двигателя увеличение тока возбуждения приводит к уменьшению угла qэл, а работа при f1=0 соответствует минимальному току статора I1 потребляемому двигателем при этом моменте. Как следует из (3.118), увеличение тока возбуждения Iв и ЭДС Е приводит к увеличению перегрузочной способности синхронного двигателя. Поэтому форсирование возбуждения при пиках нагрузки на практике используется для повышения устойчивости работы двигателя в этих режимах.

Энергетическая эффективность электропривода

Вопрос об энергетических характеристиках различных систем электропривода уже затрагивался при анализе их технических показателей в гл. 6. Однако здесь к нему необходимо вернуться и рассмотреть в более широком плане в связи с проблемой энергосбережения, острота которой в период наступления мирового энергетического кризиса резко возросла. Эта острота становится особенно понятной, если вспомнить, что электропривод потребляет свыше половины вырабатываемой в стране электроэнергии, причем, к сожалению, далеко не всегда рационально по вине, главным образом, некомпетентных или безответственных разработчиков электроприводов. Поэтому необходимо установить достоверные и удобные технические оценки энергетически эффективных вариантов электропривода, вскрыть резервы энергосбережения и наметить главные пути их реализации

При рассмотрении в §5.2 энергетики разомкнутой системы электропривоца для оценки энергетической эффективности работы электропривода было использовано общепринятое соотношение между потребляемой электроприводами мощностью Рс и полезной мощностью на рабочем органе механизма Р0 в установившихся режимах - кпд электропривода hэп:

Была подвергнута анализу известная зависимость КПД от нагрузки, обусловленная наличием постоянных потерь, для основных элементов электропривода - двигателя и передаточного механизма. Этой информации в принципе достаточно для сравнительной оценки энергетической эффективности вариантов электропривода в простейших случаях, когда электропривод работает с постоянной нагрузкой в режиме S1. При переменных значениях мощностей Pс и Рро отношение (10.1) характеризует мгновенный КПД. Поскольку на отдельных участках энергия может передаваться от рабочего органа к сети, то в этих случаях hэп отражает экономичность обратного преобразования энергии, но при этом hэп=Pc/P0.

Коэффициент полезного действия электропривода как системы, определяемый по (10.1), может быть представлен в виде произведения:

где hпр, h'дв, h'мех - соответственно КПД электрического и электромеханического преобразователей и механической части привода; Рпр - мощность на выходе электрического преобразователя; Рдв - электромагнитная механическая мощность.

При практических расчетах известны КПД двигателей и механических передач как отдельных устройств, поэтому выражение (10.2) чаще используется в записи



здесь hмех - КПД передаточного механизма; Рпр - электрическая мощность на входе двигателя; Рвдв - механическая мощность на валу двигателя.

Каждая из составляющих общего КПД - величина не постоянная, а зависящая от нагрузки каждого устройства, скорости электрических машин и других факторов. Однако исходным параметром, характеризующим каждое устройство, является номинальный КПД, соответствующий номинальной нагрузке и скорости.

Из определения КПД следует, что эта энергетическая характеристика является мерой эффективности преобразования энергии системой электропривода, мерой полезного использования потребляемой энергии.

Кроме энергетической эффективности преобразования потребляемой электроприводом энергии, важное значение имеет анализ эффективности потребления энергии от сети или автономного источника питания, т.е. характеристика электропривода как приемника электрической энергии. Экономичность передачи электроэнергии от источника электроприводу зависит как от типа и технических характеристик элементов электропривода, так и от режимов его работы. Например, энергия, затрачиваемая на возбуждение двигателей постоянного тока независимого возбуждения, идет только на потери, связанные с протеканием токов в обмотках возбуждения и созданием начального запаса электромагнитной энергии, при этом часть энергии теряется на пути от источника к электроприводу. Наиболее существенны эти потери и влияние токов намагничивания на «взаимоотношения» источника энергии и электропривода в системах, питающихся от сети переменного тока.

Напомним кратко особенности передачи и потребления электроэнергии на переменном токе. Вначале обратимся к соотношениям для однофазной цепи переменного тока.

Пусть напряжение, приложенное к фазе электрического преобразователя ЭП или непосредственно к двигателю, есть u=Umaxsin wэл, а ток, определяемый режимом ЭП или электромеханического преобразователя ЭМП, i=Imaxsin (wэлt-ф) (рис.10.1).


Мгновенная мощность, потребляемая фазой:



где U, I - действующие значения напряжения и тока.

Согласно последнему выражению мгновенная мощность может быть представлена двумя составляющими (рис.10.1,б). Одна из них в любой момент положительна, имеет среднее значение UI·cos ф, которое определяет активную мощность. Другая составляющая имеет среднее значение, равное нулю, и отражает процесс периодического обмена энергией между источником и приемником. Амплитуда переменной составляющей этой мощности UI·sin ф определяет реактивную мощность Ее наличие при питании, например, фазы двигателя переменного тока обусловлено периодическим изменением электромагнитной энергии с частотой 2wэл. Ясно, что для передачи одной и той же средней за период мощности Рcp=UI·cos ф при данном напряжении U и отсутствии реактивной составляющей мощности был бы необходимым ток Icos ф. Поскольку потери мощности в активных сопротивлениях источника, линии и приемника RS определяются полным током I, то при заданной активной мощности Рa=Рcp эти потери будут равны:



или



т.е. в 1/соs2ф раз превышать потери DРпт при передаче той же мощности постоянным током, например, при cos ф»0,7 потери DР превышают DРПТ более чем вдвое. Поэтому cos ф как энергетическая характеристика электроприводов на переменном токе определяет эффективность потребления активной мощности. При симметричном режиме асинхронных и синхронных двигателей суммарная мощность трехфазного питания будет постоянна и равна 3UI·cos ф. В этих условиях сумма мгновенных периодических составляющих P~(t) равна нулю, т.е. если по одной из фаз энергия отдается источнику с мощностью P~(t), то по двум другим в этот же момент существует поток энергии обратного направления той же мощности.

Если пока не затрагивать энергетические особенности вентильных электроприводов, можно заключить, что при выборе системы электропривода для механизмов непрерывного действия, работающих со стабильной нагрузкой на валу, удобной и достаточной оценкой энергетической эффективности электропривода являются значения КПД h3п и cos ф (последний в ряде случаев именуют коэффициентом сдвига).


Однако в большинстве случаев нагрузка электропривода в процессе его работы изменяется, соответственно меняются и значения hэп и cos ф, что существенно осложняет использование этих показателей При этом для оценки энергетической эффективности возникает необходимость перехода от мгновенных значений КПД к его интегральным значениям за определенное время. Если нагрузка электропривода изменяется циклически или проектируется электропривод циклического действия (режимы S3-S8) естественной базой для определения энергетического показателя является время цикла tц.

При этом мы должны при определении КПД электропривода соотнести полезную работу, произведенную за время tц механизмом, с энергией, потребленной за то же время электроприводом из сети:



Или, разбивая цикл на участки работы с постоянной нагрузкой



Разделив числитель и знаменатель (10.5) на tц, получим средневзвешенное за цикл значение КПД



которое может использоваться для оценки энергетической эффективности электроприводов, когда нагрузка имеет реактивный характер, а переходные процессы занимают незначительную долю времени цикла

Допустим, проектируется .нерегулируемый электропривод режима S6 при ПН=25%. Выбран асинхронный короткозамкнутый двигатель с высоким номинальным КПД, причем выбран правильно, так что в период нагрузки двигатель загружен на 95% и h=hном, равно как и для всех остальных элементов электропривода. Однако потребление в течение 75% времени цикла мощности потерь холостого хода электропривода в соответствии с (10.6) существенно снизит оценку энергетической эффективности. Возникнут варианты электропривода, в которых ее удастся повысить. Например, рассматривая формулу потерь холостого хода электропривода с асинхронным корот-козамкнутым двигателем (5.8) при s»0, w»wном, f1=f1ном, можно заключить, что потребление энергии при холостом ходе можно существенно снизить, уменьшив напряжение U1, так как DРст~Фm2, а Фm~U1. Выберем двигатель серии 4А с линейным напряжением U1л.ном=660 В при соединении в звезду и предусмотрим его питание в проектируемом электроприводе от сети U1л.ном=380 В по схеме, показанной на рис.10.2.


В этой схеме в периоды холостого хода за счет переключения обмотки статора с треугольника на звезду напряжение на фазах двигателя снижается в Ö3 раз, соответственно энергопотребление сокращается примерно в 3 раза, средневзвешенный КПД существенно увеличивается, достоверно свидетельствуя о повышении энергетической эффективности проектируемого электропривода в этом варианте.

Однако при существенном влиянии динамических нагрузок и активной статической нагрузке электропривода на одних участках цикла энергия направлена к механизму, а на других от механизма. Можно представить ситуацию, когда средняя за цикл полезная мощность может оказаться равной нулю и значение hср.ц=0 будет совершенно неверно оценивать энергетическую эффективность хорошей системы электропривода.