Основы представления графических данных
Виды компьютерной графики
Представление данных на мониторе компьютера в графическом виде впервые было реализовано в середине 50-х годов для больших ЭВМ, применявшихся в научных и военных исследованиях. С тех пор графический способ отображения данных стал неотъемлемой принадлежностью подавляющего числа компьютерных систем, в особенности персональных. Графический интерфейс пользователя сегодня является стандартом «де-факто» для программного обеспечения разных классов, начиная с операционных систем.




Отдельным предметом считается трехмерная (3D) графика, изучающая приемы и методы построения объемных моделей объектов в виртуальном пространстве. Как правило, в ней сочетаются векторный и растровый способы формирования изображений.
Особенности цветового охвата характеризуют такие понятия, как черно-белая и цветная графика. На специализацию в отдельных областях указывают названия некоторых разделов: инженерная графика, научная графика, Web-графика, компьютерная полиграфия и прочие.
Заметное место в компьютерной графике отведено развлечениям. Появилось даже такое понятие, как механизм графического представления данных ( Graphics Engine). Рынок игровых программ имеет оборот в десятки миллиардов долларов и часто инициализирует очередной этап совершенствования графики и анимации.

Растровая графика
Для растровых изображений, состоящих из точек, особую важность имеет понятие разрешения, выражающее количество точек, приходящихся на единицу длины. При этом следует различать:
• разрешение оригинала;
• разрешение экранного изображения;
• разрешение печатного изображения.
Разрешение оригинала. Разрешение оригинала измеряется в точках на дюйм (dotsper inch — dpi) и зависит от требований к качеству изображения
и размеру файла, способу оцифровки или методу создания исходной иллюстрации, избранному формату файла и другим параметрам. В общем случае действует правило: чем выше требования к качеству, тем выше должно быть разрешение оригинала.
Разрешение экранного изображения. Для экранных копий изображения элементарную точку растра принято называть пикселом. Размер пиксела варьируется в зависимости от выбранного экранного разрешения (из диапазона стандартных значений), разрешения оригинала и масштаба отображения.
Мониторы для обработки изображений с диагональю 20-21 дюйм (профессионального класса), как правило, обеспечивают стандартные экранные разрешения 640x480, 800x600, 1024x768, 1280x1024, 1600x1200, 1600x1280, 1920x1200, 1920x1600 точек.
Расстояние между соседними точками люминофора у качественного монитора составляет 0,22-0,25 мм.
Для экранной копии достаточно разрешения 72 dpi, для распечатки на цветном или лазерном принтере 150-200 dpi, для вывода на фотоэкспонирующем устройстве 200-300 dpi. Установлено эмпирическое правило, что при распечатке величина разрешения оригинала должна быть в 1,5 раза больше, чем линиатура растра устройства вывода. В случае, если твердая копия будет увеличена по сравнению с оригиналом, эти величины следует умножить на коэффициент масштабирования.
Разрешение печатного изображения и понятие линиатуры. Размер точки растрового изображения как на твердой копии (бумага, пленка и т. д.), так и на экране зависит от примененного метода и параметров растрирования оригинала. При растрировании на оригинал как бы накладывается сетка линий, ячейки которой образуют элемент растра. Частота сетки растра измеряется числом линий на дюйм (lines per inch — Ipi) и называется линиатурой.
Размер точки растра рассчитывается для каждого элемента и зависит от интенсивности тона в данной ячейке. Чем больше интенсивность, тем плотнее заполняется элемент растра. То есть, если в ячейку попал абсолютно черный цвет, размер точки растра совпадет с размером элемента растра. В этом случае говорят о 100% заполняемое™. Для абсолютно белого цвета значение заполняемости составит 0%. На практике заполняемость элемента на отпечатке обычно составляет от 3 до 98%. При этом все точки растра имеют одинаковую оптическую плотность, в идеале приближающуюся к абсолютно черному цвету. Иллюзия более темного тона создается за счет увеличения размеров точек и, как следствие, сокращения пробельного поля между ними при одинаковом расстоянии между центрами элементов растра (рис. 15.1). Такой метод называют растрированием с амплитудной модуляцией (AM).
Существует и метод растрирования с частотной модуляцией (ЧМ), когда интенсивность тона регулируется изменением расстояния между соседними точками одинакового размера. Таким образом, при частотно-модулированном растрировании в ячейках растра с разной интенсивностью тона находится разное число точек (см.
рис. 15.1).
 |
Рис. 15.1. Примеры амплитудной и частотной модуляции растра
Изображения, растрированные ЧМ-методом, выглядят более качественно, так как размер точек минимален и во всяком случае существенно меньше, чем средний размер точки при AM-растрировании. Еще более повышает качество изображения разновидность ЧМ-метода, называемая стохастическим растрированием. В этом случае рассчитывается число точек, необходимое для отображения требуемой интенсивности тона в ячейке растра. Затем эти точки располагаются внутри ячейки на расстояниях, вычисленных квазислучайным методом (на самом деле используется специальный математический алгоритм). То есть регулярная структура растра внутри ячейки, как и на изображении в целом, вообще отсутствует (рис. 15.2). Поэтому при стохастическом ЧМ-растрировании теряет смысл понятие линиатуры растра, имеет значение лишь разрешающая способность устройства вывода. Такой способ требует больших затрат вычислительных ресурсов и высокой точности полиграфического оборудования; он применяется в основном для художественных работ, при печати с числом красок, превышающим четыре.
 |
Интенсивность тона (так называемую светлоту) принято подразделять на 256 уровней. Большее число градаций не воспринимается зрением человека и является избыточным. Меньшее число ухудшает восприятие изображения (минимально допустимым для качественной полутоновой иллюстрации принято значение 150 уровней). Нетрудно подсчитать, что для воспроизведения 256 уровней тона достаточно иметь размер ячейки растра 256 = 16 х 16 точек.
Между разрешением оригинала, частотой растра и градацией уровней существует зависимость, описываемая формулой:

где N — число градаций уровней тона (оттенков),
dpi — разрешение устройства вывода (отображения),
Ipi — линиатура растра. Единица в формуле соответствует абсолютно белому цвету, когда ячейка растра вообще не заполнена.
При выводе копии изображения на принтере или полиграфическом оборудовании линиатуру растра выбирают, исходя из компромисса между требуемым качеством, возможностями аппаратуры и параметрами печатных материалов. Для лазерных принтеров рекомендуемая линиатура составляет 65-100 Ipi, для газетного производства — 65-85 Ipi, для книжно-журнального — 85-133 Ipi, для художественных и рекламных работ — 133-300 Ipi.
При печати изображений с наложением растров друг на друга, например многоцветных, каждый последующий растр поворачивается на определенный угол. Традиционными для цветной печати считаются углы поворота: 105 градусов для голубой печатной формы, 75 градусов для пурпурной, 90 градусов для желтой и 45 градусов для черной. При этом ячейка растра становится косоугольной, и для воспроизведения 256 градаций тона с линиатурой 150 Ipi уже недостаточно разрешения 16x150=2400 dpi. Поэтому для фотоэкспонирующих устройств профессионального класса принято минимальное стандартное разрешение 2540 dpi, обеспечивающее качественное растрирование при разных углах поворота растра. Таким образом, коэффициент, учитывающий поправку на угол поворота растра, для цветных изображений составляет 1,06.
Динамический диапазон. Качество воспроизведения тоновых изображений принято оценивать динамическим диапазоном (D). Это оптическая плотность, численно равная десятичному логарифму величины, обратной коэффициенту пропускания т (для оригиналов, рассматриваемых «на просвет», например слайдов) или коэффициенту отражения р (для прочих оригиналов, например полиграфических отпечатков):

где FQ — падающий световой поток,
Fp — отраженный световой поток,
T — пропущенный световой поток.
Для оптических сред, пропускающих свет, динамический диапазон лежит в пределах от 0 до 4. Для поверхностей, отражающих свет, значение динамического диапазона составляет от 0 до 2.
Чем выше динамический диапазон, тем большее число полутонов присутствует в изображении и тем лучше качество его восприятия.
Связь между параметрами изображения и размером файла. Средствами растровой графики принято иллюстрировать работы, требующие высокой точности в передаче цветов и полутонов. Однако размеры файлов растровых иллюстраций стремительно растут с увеличением разрешения. Фотоснимок, предназначенный для домашнего промотра (стандартный размер 10x15 см, оцифрованный с разрешением 200-300 dpi, цветовое разрешение 24 бита), занимает в формате TIFF с включенным режимом сжатия около 4 Мбайт. Оцифрованный с высоким разрешением слайд занимает 45-50 Мбайт. Цветоделенное цветное изображение формата А4 занимает 120-150 Мбайт.
Масштабирование растровых изображений. Одним из недостатков растровой графики является так называемая пикселизация изображений при их увеличении (если не приняты специальные меры). Раз в оригинале присутствует определенное количество точек, то при большем масштабе увеличивается и их размер, становятся заметны элементы растра, что искажает саму иллюстрацию (рис. 15.3). Для противодействия пикселизации принято заранее оцифровывать оригинал с разрешением, достаточным для качественной визуализации при масштабировании. Другой прием состоит в применении стохастического растра, позволяющего уменьшить эффект пикселизации в определенных пределах. Наконец, при масштабировании используют метод интерполяции, когда увеличение размера иллюстрации происходит не за счет масштабирования точек, а путем добавления необходимого числа промежуточных точек.
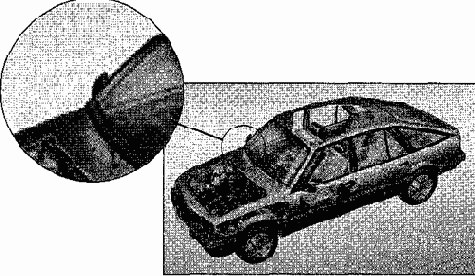
Рис. 153. Эффект пикселизации при масштабировании растрового
изображения
Векторная графика
Если в растровой графике базовым элементом изображения является точка, то в векторной графике—линия. Линия описывается математически как единый объект, и потому объем данных для отображения объекта средствами векторной графики существенно меньше, чем в растровой графике.
Линия — элементарный объект векторной графики.
Как и любой объект, линия обладает свойствами: формой (прямая, кривая), толщиной, цветом, начертанием (сплошная, пунктирная). Замкнутые линии приобретают свойство заполнения. Охватываемое ими пространство может быть заполнено другими объектами {текстуры, карты) или выбранным цветом.
Простейшая незамкнутая линия ограничена двумя точками, именуемыми узлами. Узлы также имеют свойства, параметры которых влияют на форму конца линии и характер сопряжения с другими объектами.
Все прочие объекты векторной графики составляются из линий. Например куб можно составить из шести связанных прямоугольников, каждый из которых, в свою очередь, образован четырьмя связанными линиями. Возможно представить куб и как двенадцать связанных линий, образующих ребра.
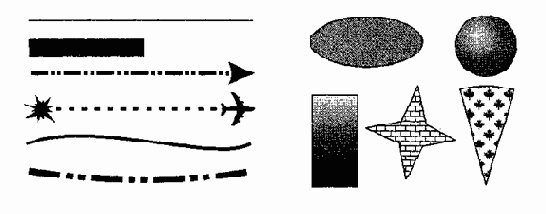
Рис. 15.4. Объекты векторной графики
Математические основы векторной графики
Рассмотрим подробнее способы представления различных объектов в векторной графике.
Точка. Этот объект на плоскости представляется двумя числами (х, у), указывающими его положение относительно начала координат.
Прямая линия. Ей соответствует уравнение у = kx + b. Указав параметры k и Ь, всегда можно отобразить бесконечную прямую линию в известной системе координат, то есть для задания прямой достаточно двух параметров.
Отрезок прямой. Он отличается тем, что требует для описания еще двух параметров — например, координат xl и х2 начала и конца отрезка.
Кривая второго порядка. К этому классу кривых относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба. Прямые линии являются всего лишь частным случаем кривых второго порядка. Формула кривой второго порядка в общем виде может выглядеть, например, так:

Таким образом, для описания бесконечной кривой второго порядка достаточно пяти параметров. Если требуется построить отрезок кривой, понадобятся еще два параметра.
Кривая третьего порядка. Отличие этих кривых от кривых второго порядка состоит в возможном наличии точки перегиба.
Например график функции у=х? имеет точку перегиба в начале координат (рис. 15.5). Именно эта особенность позволяет сделать кривые третьего порядка основой отображения природных объектов в векторной графике. Например линии изгиба человеческого тела весьма близки к кривым третьего порядка. Все кривые второго порядка, как и прямые, являются частными случаями кривых третьего порядка.
В общем случае уравнение кривой третьего порядка можно записать так:

Таким образом, кривая третьего порядка описывается девятью параметрами. Описание ее отрезка потребует на два параметра больше.
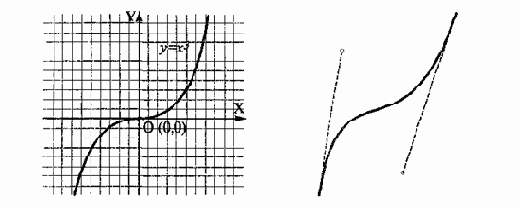
Рис. 15.5. Кривая третьего порядка (слева) и кривая Безье (справа)
Кривые Безье. Это особый, упрощенный вид кривых третьего порядка (см. рис. 15.5). Метод построения кривой Безье (Bezier) основан на использовании пары касательных, проведенных к отрезку линии в ее окончаниях. Отрезки кривых Безье описываются восемью параметрами, поэтому работать с ними удобнее. На форму линии влияет угол наклона касательной и длина ее отрезка. Таким образом, касательные играют роль виртуальных «рычагов», с помощью которых управляют кривой.
Фрактальная графика
Фрактальная графика, как и векторная, основана на математических вычислениях. Однако базовым элементом фрактальной графики является сама математическая формула, то есть никаких объектов в памяти компьютера не хранится и изображение строится исключительно по уравнениям. Таким способом строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие природные ландшафты и трехмерные объекты (рис. 15.6).
Основные понятия трехмерной графики
Трехмерная графика нашла широкое применение в таких областях, как научные расчеты, инженерное проектирование, компьютерное моделирование физических объектов. В качестве примера рассмотрим наиболее сложный вариант трехмерного моделирования — создание подвижного изображения реального физического тела.

Рис. 15.6. Примеры фрактальных объектов
В упрощенном виде для пространственного моделирования объекта требуется:
• спроектировать и создать виртуальный каркас («скелет») объекта, наиболее полно соответствующий его реальной форме;
• спроектировать и создать виртуальные материалы, по физическим свойствам визуализации похожие на реальные;
 |
• настроить физические параметры пространства, в котором будет действовать объект, - задать освещение, гравитацию, свойства атмосферы, свойства взаимодействующих объектов и поверхностей;
• задать траектории движения объектов;
• рассчитать результирующую последовательность кадров;
• наложить поверхностные эффекты на итоговый анимационный ролик.
Для создания реалистичной модели объекта используют геометрические примитивы (прямоугольник, куб, жар, конус и прочие) и гладкие, так называемые онлайновые поверхности. В последнем случае применяют чаще всего метод бикубических рациональныхВ-сплайнов на неравномерной сетке (NURBS). Вид поверхности при этом определяется расположенной в пространстве сеткой опорных точек. Каждой точке присваивается коэффициент, величина которого определяет степень ее влияния на часть поверхности, проходящей вблизи точки. От взаимного расположения точек и величины коэффициентов зависит форма и «гладкость» поверхности в целом. Специальный инструментарий позволяет обрабатывать примитивы, составляющие объект, как единое целое, с учетом их взаимодействия на основе заданной физической модели.
Деформация объекта обеспечивается перемещением кон ii»r къчых точек, расположенных вблизи. Каждая контрольная точка связана с f4, i ежащими опорными точками, степень ее влияния на них определяется удаленн i- , Другой метод называют сеткой деформации. Вокруг объекта или его частк - щается трехмерная сетка, перемещение любой точки которой вызывает упруг t< 1 эрмацию как самой сетки, так и окруженного объекта.
Еще одним способом построения объектов из примитивов служит твердотельное моделирование. Объекты представлены твердыми телами, которые при взаимодействии с другими телами различными способами (объединение, вычитание, слияние и другие) претерпевают необходимую трансформацию.
Например, вычитание из прямоугольного параллелепипеда шара приведет к образованию в параллелепипеде полукруглой лунки.
После формирования «скелета» объекта необходимо покрыть его поверхность материалами. Все многообразие свойств в компьютерном моделировании сводится к визуализации поверхности, то есть к расчету коэффициента прозрачности поверхности и угла преломления лучей света на границе материала и окружающего пространства. Для построения поверхностей материалов используют пять основных физических моделей:
• Bouknight — поверхности с диффузным отражением без бликов (например, матовый пластик);
• Phong—поверхности со структурированными микронеровностями (например, металлические);
• Blinn — поверхности со специальным распределением микронеровностей с учетом взаимных перекрытий (например, глянец);
• Whitted — модель, позволяющая дополнительно учитывать поляризацию света;
 |
Закраска поверхностей осуществляется методами Гуро (Gouraud) или Фонга (Phong). В первом случае цвет примитива рассчитывается лишь в его вершинах, а затем линейно интерполируется по поверхности. Во втором случае строится нормаль к объекту в целом, ее вектор интерполируется по поверхности составляющих примитивов и освещение рассчитывается для каждой точки.
Свет, уходящий с поверхности в конкретной точке в сторону наблюдателя, представляет собой сумму компонентов, умноженных на коэффициент, связанный с материалом и цветом поверхности в данной точке. К таковым компонентам относятся:
• свет, пришедший с обратной стороны поверхности, то есть преломленный свет {Refracted);
• свет, равномерно рассеиваемый поверхностью (Diffuse);
• зеркально отраженный свет (Reflected);
• блики, то есть отраженный свет источников (Specular);
• собственное свечение поверхности (Self Illumination).
 |
Следующим этапом является наложение («проектирование») текстур на определенные участки каркаса объекта. При этом необходимо учитывать их взаимное влияние на границах примитивов. Проектирование материалов на объект — задача трудно формализуемая, она сродни художественному процессу и требует от исполнителя хотя бы минимальных творческих способностей.
Из всех параметров пространства, в котором действует создаваемый объект, с точки зрения визуализации самым важным является определение источников света. В трехмерной графике принято использовать виртуальные эквиваленты физических источников.
• Аналогом равномерного светового фона служит так называемый растворенный свет (Ambient Light), Он не имеет геометрических параметров и характеризуется только цветом и интенсивностью. Пример в природе — естественная освещенность вне видимости Солнца и Луны.
• Удаленный не точечный источник называют удаленным светом (Distant Light). Ему присваиваются конкретные геометрические параметры (координаты). Аналог в природе — Солнце.
• Точечный источник света (Point Light Source) равномерно испускает свет во всех направлениях и также имеет координаты. Аналог в технике — электрическая лампочка.
• Направленный источник света (Direct Light Source) кроме местоположения характеризуется направлением светового потока, углами раствора полного конуса света и его наиболее яркого пятна. Аналог в технике — прожектор.
После завершения конструирования и визуализации объекта приступают к его «оживлению», то есть заданию параметров движения.
Компьютерная анимация базируется на ключевых кадрах. В первом кадре объект выставляется в исходное положение. Через определенный промежуток (например, в восьмом кадре) задается новое положение объекта и так далее до конечного положения. Промежуточные значения вычисляет программа по специальному алгоритму. При этом происходит не просто линейная аппроксимация, а плавное изменение положения опорных точек объекта в соответствии с заданными условиями (рис. 15.7).
Ключевые кадры
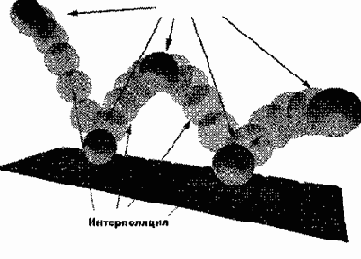
Рис. 15.7. Построение видеоряда по ключевым кадрам
Эти условия определяются иерархией объектов (то есть законами их взаимодействия между собой), разрешенными плоскостями движения, предельными углами поворотов, величинами ускорений и скоростей. Такой подход называют методом инверсной кинематики движения. Он хорошо работает при моделировании механических устройств. В случае с имитацией живых объектов используют так называемые скелетные модели. То есть, создается некий каркас, подвижный в точках, характерных для моделируемого объекта. Движения точек просчитываются предыдущим методом. Затем на каркас накладывается оболочка, состоящая из смоделированных поверхностей, для которых каркас является набором контрольных точек, то есть создается каркасная модель. Каркасная модель визуализуется наложением поверхностных текстур с учетом условий освещения. В ходе перемещения объекта получается весьма правдоподобная имитация движений живых существ.
Наиболее совершенный метод анимации заключается в фиксации реальных движений физического объекта. Например, на человеке закрепляют в контрольных точках яркие источники света и снимают заданное движение на видео- или кинопленку. Затем координаты точек по кадрам переводят с пленки в компьютер и присваивают соответствующим опорным точкам каркасной модели. В результате движения имитируемого объекта практически неотличимы от живого прототипа.
Процесс расчета реалистичных изображений назиъают рендерингом (визуализацией).
Большинство современных программ рендеринга основаны на методе обратной трассировки лучей (Backway Ray Tracing). Его суть заключается в следующем.
1.Из точки наблюдения сцены посылается в пространство виртуальный луч, по
траектории которого должно прийти изображение в точку наблюдения.
2.Для определения параметров приходящего луча все объекты сцены проверяются
на пересечение с траекторией наблюдения. Если пересечения не происходит,
считается, что луч попал в фон сцены и приходящая информация определяется
только параметрами фона. Если траектория пересекается с объектом, то в точке соприкосновения рассчитывается свет, уходящий в точку наблюдения в соответствии с параметрами материала.
3.Сначала просчитывается преломленный и отраженный свет, затем проверяется видимость из точки пересечения всех источников света и интенсивность светового потока. Также вычисляются наличие, резкость и ширина бликов от каждого источника света.
4.Полученные в результате итоговые значения цвета и интенсивности обрабатываются с учетом траектории луча и параметров атмосферы, и присваиваются точке объекта как значения визуализации для наблюдателя. Затем процесс повторяется для всех элементов сцены. С целью упрощения расчетов пересечение проверяют не для каждой точки, а для примитива в целом. Иногда вокруг объекта создают простую виртуальную геометрическую фигуру (параллелепипед, шар), расчет пересечений для объекта выполняют только при пересечении траектории наблюдения с фигурой в целом.
Применение сложных математических моделей позволяет имитировать такие физические эффекты, как взрывы, дождь, огонь, дым, туман. Существуют методы расчета процедурных эффектов (Procedural Effects) и взаимодействия систем частиц (Particle System). Однако их применение в полном объеме требует громадных вычислительных ресурсов, и потому в персональных компьютерах обычно используют упрощенные варианты. По завершении рендеринга компьютерную трехмерную анимацию используют либо как самостоятельный продукт, либо в качестве отдельных частей или кадров готового продукта (рис. 15.8).
Особую область трехмерного моделирования в режиме реального времени составляют тренажеры технических средств — автомобилей, судов, летательных и космических аппаратов. В них необходимо очень точно реализовывать технические параметры объектов и свойства окружающей физической среды. В более простых вариантах, например при обучении вождению наземных транспортных средств, тренажеры реализуют на персональных компьютерах.
Самые совершенные на сегодняшний день устройства созданы для обучения пилотированию космических кораблей и военных летательных аппаратов. Моделированием и визуализацией объектов в таких тренажерах заняты несколько специализированных графических станций, построенных на мощных Ж5С-процессорах и скоростных видеоадаптерах с аппаратными ускорителями трехмерной графики. Общее управление системой и просчет сценариев взаимодействия возложены на суперкомпьютер, состоящий из десятков и сотен процессоров. Стоимость таких комплексов выражается девятизначными цифрами, но их применение окупается достаточно быстро, так как обучение на реальных аппаратах в десятки раз дороже.
 |
Программные средства обработки трехмерной графики
На персональных компьютерах основную долю рынка программных средств обработки трехмерной графики занимают три пакета. Эффективней всего они работают на самых мощных машинах (в двух- или четырехпроцессорных конфигурациях Pentium II/III, Xeon) под управлением операционной системы Windows NT.
Программа создания и обработки трехмерной графики 3D Studio Max фирмы Kinetix изначально создавалась для платформы Windows. Этот пакет считается «полупрофессиональным». Однако его средств вполне хватает для разработки качественных трехмерных изображений объектов неживой природы (рис, 15.9). Отличительными особенностями пакета являются поддержка большого числа аппаратных ускорителей трехмерной графики, мощные световые эффекты, большое число дополнений, созданных сторонними фирмами.
Сравнительная нетребовательность к аппаратным ресурсам позволяет работать даже на компьютерах среднего уровня. Вместе с тем по средствам моделирования и анимации пакет 3D Studio Max уступает более развитым программным средствам.
 |
3D Studio Max
Программа Softimage 3D компании Microsoft изначально создавалась для рабочих станций SGIw. лишь сравнительно недавно была конвертирована под операционную систему Windows NT. Программу отличают богатые возможности моделирования, наличие большого числа регулируемых физических и кинематографических параметров. Для рендеринга применяется качественный и достаточно быстрый модуль Mental Ray. Существует множество дополнений, выпущенных «третьими» фирмами, значительно расширяющих функции пакета. Эта программа считается стандартом «де-факто» в мире специализированных графических станций SGI, а на платформе IBM PC выглядит несколько тяжеловато и требует мощных аппаратных ресурсов.
Наиболее революционной с точки зрения интерфейса и возможностей является программа Maya, разработанная консорциумом известных компаний (Alias, Wavefront, TDI). Пакет существует в вариантах для разных операционных систем, в том числе и Windows NT. Он имеет модульное построение и включает следующие блоки.
• Base — содержит ядро программы. Обеспечивает поддержку основных инструментов моделирования, инверсной кинематики, обработки звука, имитации физических твердых тел, захвата движения, рендеринга и основных наборов эффектов.
• Maya F/X — набор дополнительных модулей, поддерживающих эффекты обработки систем частиц и моделирования физики взаимодействия мягких тел.
• Maya Power Modeler — в основном содержит мощные средства полигонального и сплайнового моделирования объектов;
• Maya Artisan — наиболее передовой модуль, позволяющий обрабатывать виртуальные модели методами, характерными для реальной работы скульпторов и художников.
Позволяет, к примеру, рисовать по поверхности объекта «кистями», сглаживать поверхности или делать их более шероховатыми «скульптурными резцами»;
• Maya Cloth — предназначен для моделирования одежды;
• Maya Fur — модуль для имитации поверхностей, покрытых шерстью или мехом (рис. 15.10);
•

Рис. 15.10. Моделирование меховой поверхности средствами пакета Maya
• Maya Live — сценарный модуль, обеспечивающий сопряжение реальных съемок (на «натуре») с компьютерной анимацией.
Инструментарий Maya сведен в четыре группы: Animation (анимация), Modeling (моделирование), Dynamic (физическое моделирование), Rendering (визуализация). Удобный настраиваемый интерфейс выполнен в соответствии с современными требованиями. На сегодняшний день Maya является наиболее передовым пакетом в классе средств создания и обработки трехмерной графики для персональных компьютеров.
