Арифметико-логические устройства
Ранее были рассмотрены схемы, осуществляющие суммирование многоразрядных кодов. Однако кроме суммирования часто требуется осуществлять не только суммирование, но и вычитание двоичных кодов. , при помощи которых можно записывать отрицательные числа уже рассматривались в предыдущих лекциях. Там же было показано, что при использовании дополнительных кодов операцию вычитания двух положительных чисел можно заменить операцией суммирования положительного и отрицательного числа, при этом получение отрицательного числа из положительного числа является элементарной операцией. Для этого необходимо проинвертировать число и прибавить к нему 1.
Схема вычитателя числа A из числа B приведена на рисунке 1, а схема вычитателя числа B из числа A приведена на рисунке 2.

Рисунок 1. Схема вычитателя числа A из числа B.

Рисунок 2. Схема вычитателя числа B из числа A.
Если же потребуется в процессе вычислений изменять арифметическую операцию, то в схему можно ввести коммутатор. Такая схема приведена на рисунке 3.

Рисунок 3. Структурная схема арифметического устройства.
В приведённой на рисунке 3 схеме используются четырёхвходовые коммутаторы, для управления каждым из которых достаточно двух бит. То есть для управления всей схемы в целом достаточно четырёх проводов управления. Попытаемся построить таблицу операций, которые будет выполнять эта схема. На результат операции будет влиять вход переноса сумматора PI, поэтому этот провод тоже включим в состав кода, управляющего схемой. Операции, которые выполняются арифметической схемой в зависимости от поданного на управляющие линии кода, приведены в таблице 1.
Проанализируем эту таблицу. Если на все управляющие входы подать низкий потенциал, то к входу сумматора будут подключены коды A и B без инверсии. В этом случае будет производиться операция суммирования. Эта ситуация отображена первыми двумя строками таблицы выполняемых операций. Операция вычитания осуществляется второй, третьей, восьмой и девятой строкой. В этом случае один из операндов поступает на вход сумматора через блок инверторов.
Правда для получения дополнительного кода не хватает единицы, но её можно подать на вход переноса сумматора PI. Ещё одной часто используемой операцией является увеличение числа на единицу или уменьшение числа на единицу. Эти операции позволяют легко организовывать циклы в программе и переходить от предыдущего операнда к следующему. Такие операции могут быть выполнены при помощи кодов, записанных в строках четыре, семь, шестнадцать и двадцать пять. Кроме того, схема арифметического устройства может просто передавать на выход любой из входных кодов без изменения, что позволяет осуществлять копирование данных (суммирование с константой ноль) через это устройство без дополнительных схем коммутации.

При небольшом изменении схемы такое устройство может быть преобразовано в схему, которая позволяет осуществлять не только арифметические, но и логические операции. Для этого нужно вести дополнительный коммутатор, который будет разрывать цепи переноса между разрядами. Эта управляющая цепь обычно называется M.
Подчеркнём основную особенность полученного устройства. Арифметико-логические устройства позволяют выбирать вид выполняемой операции при помощи кода, подаваемого на специальные ножки микросхемы. Это позволяет программировать одно и то же устройство для выполнения различных функций. Разработка такого устройства позволило обменивать большую скорость выполнения отдельных операций на сложность реализуемого алгоритма, что, в конце концов, привело к разработке микропроцессорных систем. Развитие этих систем изменило окружающий нас мир.
[ ]
Декодеры
Декодеры (дешифраторы) позволяют преобразовывать одни виды двоичных кодов в другие. Преобразование производится по правилам, описанным в таблицах истинности, поэтому построение дешифраторов не представляет трудностей. Для построения дешифратора можно воспользоваться правилами .
Рассмотрим пример построения декодера из двоичного кода в десятичный. Таблица истинности такого декодера приведена на рисунке 1.
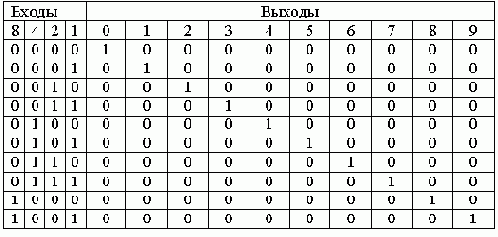
Рисунок 1. Таблица истинности десятичного декодера.
В соответствии с принципами по произвольной таблице истинности получим схему декодера, реализующего таблицу истинности, приведённую на рисунке 1. Эта схема приведена на рисунке 2.

Рисунок 2. Принципиальная схема двоично-десятичного декодера.
Точно так же можно получить схему для любого другого декодера или дешифратора.
Дешифраторы выпускаются в виде отдельных микросхем или используются в составе других микросхем, таких как мультиплексоры или ПЗУ. Изображение дешифратора на принципиальных схемах приведено на рисунке 3. На этом рисунке приведено обозначение двоично-десятичного дешифратора, принципиальная схема которого изображена на рисунке 2.
Рисунок 3. Изображение двоично-десятичного дешифратора на принципиальных схемах.
[ ] [ ] [ ]
Демультиплексоры
Задача передачи сигнала с одного входа микросхемы на один из нескольких выходов называется демультиплексированием. Демультиплексор можно построить на основе точно таких же схем логического "И", как и при построении мультиплексора. Существенным отличием от мультиплексора является возможность объединения нескольких входов в один без дополнительных схем. Однако для увеличения нагрузочной способности микросхемы, на входе демультиплексора для усиления входного сигнала лучше поставить инвертор.
Схема демультиплексора приведена на рисунке 5. В этой схеме для выбора конкретного выхода демультиплексора, как и в мультиплексоре, используется двоичный дешифратор.
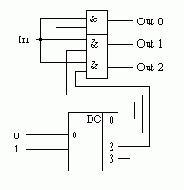
Рисунок 5. Принципиальная схема демультиплексора, управляемого двоичным кодом.
На принципиальных схемах демультиплексор обычно изображается точно так же как и . Единственное отличие в изображении схемы – это наличие дополнительного информационного входа.
[] [] [
Двоичные асинхронные счётчики
Простейший вид счётчика - двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера можно воспользоваться универсальным D-триггером с обратной связью, как это показано на рисунке 1.

Рисунок 1 Построение счетного T-триггера на универсальном D-триггере.
В этой схеме, так как на вход триггера подается сигнал с инверсного выхода микросхемы, при поступлении тактовых импульсов сигнал на выходе будет меняться с 0 на 1 и наоборот. Временная диаграмма сигналов на входе и выходах триггера приведена на рисунке 2.

Таким образом у нас появился счётчик, считающий до двух. Обычно требуется посчитать количество импульсов, которое больше двух. В этом случае можно использовать выходной сигнал счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два.

Схема счётчика, позволяющего посчитать до 16 импульсов приведена на рисунке 3, а временная диаграмма сигналов на входе и выходах этого счётчика приведена на рисунке 4.

Рисунок 3 Схема четырёхразрядного счётчика, построенного на универсальных D-триггерах.

Рисунок 4 Временная диаграмма четырёхразрядного счётчика.
Как видно из временной диаграммы, на выходах этого двоичного счётчика последовательно появляются цифры от 0 до 15. Естественно эти цифры записаны в двоичном виде. Они приведены в таблице 1. То есть, при поступлении на счётный вход очередного импульса, содержимое счётчика увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.
Таблица 1. Изменение уровней на выходе суммирующего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
Существуют готовые микросхемы асинхронных двоичных счётчиков. Классическим примером такого счётчика является микросхема 555ИЕ5. Её изображение на принципиальных схемах приведено на рисунке 5. В этой микросхеме существует вход обнуления микросхемы R, который позволяет записать во все триггеры счётчика нулевое значение.
Рисунок 5. Четырёхразрядный двоичный счётчик.
Двоичные вычитающие асинхронные счётчики
Счётчики могут не только увеличивать своё значение на единицу при поступлении на вход импульсов но и уменьшать его. Такие счётчики получили название вычитающих счётчиков. Для реализации вычитающего счётчика достаточно чтобы T-триггер срабатывал по переднему фронту входного сигнала. Это можно осуществить инвертированием этого сигнала. В схеме, приведенной на рисунке 6, для реализации вычитающего счётчика сигнал на входы последующих триггеров подаются с инверсных выводов предыдущих триггеров.

Рисунок 6 Схема четырёхразрядного двоичного вычитающего счётчика, построенного на универсальных D-триггерах.
Временная диаграмма этого счётчика приведена на рисунке 7. По этой диаграмме видно, что при поступлении на вход счётчика первого же импульса на выходах появляется максимально возможное для четырёхразрядного счётчика число 15. При поступлении следующих импульсов содержимое счётчика уменьшается на единицу. Этот процесс продолжается до тех пор, пока содержимое счётчика не станет вновь равно 0.

Рисунок 7. Временная диаграмма четырёхразрядного вычитающего счётчика.
Все возможные состояния сигналов на выходах счётчика при поступлении импульсов на вход микросхемы приведены в таблице 2:
Таблица 2. Изменение уровней на выходе вычитающего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 0 | 1 | 1 | 1 |
| 10 | 0 | 1 | 1 | 0 |
| 11 | 0 | 1 | 0 | 1 |
| 12 | 0 | 1 | 0 | 0 |
| 13 | 0 | 0 | 1 | 1 |
| 14 | 0 | 0 | 1 | 0 |
| 15 | 0 | 0 | 0 | 1 |
Для тех, кто привык работать с реально выпускаемыми микросхемами, следует обратить внимание, что для примера были использованы D-триггеры, работающие по заднему фронту. Микросхемы 1533ТМ2 (два D-триггера в одном корпусе) срабатывают по переднему фронту, поэтому схемы для суммирующего и вычитающего счётчика поменяются местами.
[ ] [ ] [ ]
Газоразрядные лампы
Эти индикаторы в отличие от ламп накаливания управляются не напряжением, а током. Поэтому в схему приходится вводить токоограничивающий резистор. Схема включения газоразрядного индикатора приведена на рисунке 2.
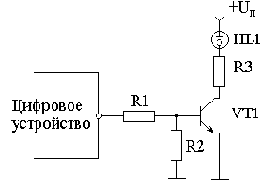
В этой схеме транзистор требуется в основном для согласования по напряжению, так как газоразрядные индикаторы питаются от напряжения 180 ... 300 В.
Это более экономичные индикаторы по сравнению с лампами накаливания, но использование высокого напряжения питания привело к тому, что они в настоящее время практически не используются.
В настоящее время практически везде используются светодиоды и жидкокристаллические индикаторы.
[ ]
Генераторы периодических сигналов
При работе цифровых схем часто возникает задача синхронизации моментов изменения или записи сигналов. Для этого можно воспользоваться любым известным генератором сигналов, в том числе построенным на одиночном транзисторе или операционном усилителе. Однако в этом случае потребуется специальное устройство преобразования выходного сигнала генератора к цифровым логическим уровням, используемым в разрабатываемой схеме.
Намного проще использовать для построения генераторов цифрового сигнала логические элементы. Как известно из общей теории построения генераторов сигналов, для самовозбуждения генераторов необходимо выполнить два условия: баланс фаз и баланс амплитуд. Так как любые логические элементы обладают усилением, то для построения генераторов можно использовать как инверторы, так и схемы логического "И" и "ИЛИ". В некоторых случаях для построения генераторов используют даже триггеры.
Рассмотрим схему простейшего генератора. Для его реализации необходимо обеспечить баланс фаз на заданной частоте. Генератор может быть выполнен по схеме индуктивной или ёмкостной трёхточки. Такие схемы называются осцилляторными. В настоящее время обычно используется схема ёмкостной трёхточки как более дешёвый вариант. На рисунке 1 приведена подобная схема, выполненная на биполярном транзисторе.

Рисунок 1. Ёмкостная трёхточка, выполненная на биполярном транзисторе.
В этой схеме усилительный элемент включен в схему контура L1 C2 C3, резонансная частота которого и задаёт частоту генерации схемы. Глубина обратной связи задаётся соотношением ёмкостей этого контура и коэффициентом усиления транзистора на заданной частоте. Точно так же можно построить генератор и на основе . Схема LC генератора, построенного на основе логического инвертора, приведена на рисунке 2.

Рисунок 2. Ёмкостная трёхточка, выполненная на логическом инверторе.
При реализации генераторов на логических элементах необходимо следить за тем, чтобы при запуске генератора логический элемент находился в активном режиме.
В обычном включении логический инвертор находится в режиме ограничения. В режиме ограничения осуществляется жесткий режим запуска генератора, поэтому для возникновения колебаний в такой схеме потребуется подать мощный импульс на вход инвертора. Для самопроизвольного возникновения колебаний в схеме генератора необходимо перевести логический элемент в усилительный режим. Для этого инвертор необходимо охватить отрицательной обратной связью по постоянному току. В приведённой на рисунке 2 схеме это осуществляется замыканием входа и выхода микросхемы через индуктивность L1. Второй инвертор требуется для доведения уровня генерируемого сигнала до цифровых логических уровней. То есть он используется в качестве развязывающего (буферного) усилителя.
Схема на одном инверторе чаще всего используется для построения кварцевых генераторов. В этом случае в ёмкостной трёхточке вместо индуктивности используется кварцевый резонатор. Схема кварцевого генератора на одном логическом инверторе приведена на рисунке 3.

Рисунок 3. Схема кварцевого генератора, выполненная на логическом инверторе.
Ёмкости в частотозадающей цепочке обычно выбираются в пределах от 10 до 30 пФ. Соотношение ёмкостей задаёт глубину обратной связи, а значит устойчивость запуска генератора в диапазоне температур. Кварцевый резонатор не пропускает постоянный ток, поэтому в кварцевом генераторе для обеспечения автоматического запуска генератора приходится использовать дополнительные резисторы. Именно соотношение этих резисторов определяет коэффициент усиления активного элемента генераторов. При использовании очень высокочастотных кварцевых резонаторов резистор R1 для облегчения самовозбуждения генератора может отсутствовать.
Достаточно часто возникает необходимость останавливать генератор для экономии потребления электроэнергии. В этом случае вместо логического инвертора можно использовать схему "И". Подобная схема приведена на рисунке 4. Именно такая схема используется внутри современных микросхем в качестве задающего тактового генератора.

Рисунок 4. Схема кварцевого генератора, выполненная на элементе логического "И".
Индикаторы
Индикаторы предназначены для отображения различных видов информации для человека. Простейший вид информации - это двоичная информация. Например цел предохранитель или вышел из строя, включено питание или нет, задействован режим передачи или нет. Для отображения такой информации можно воспользоваться единичными индикаторами, такими как малогабаритные лампочки накаливания, газоразрядные лампы, жидкокристаллические индикаторы или светодиоды. Рассмотрим подробнее преимущества и недостатки каждого из этих видов индикаторов.
Логические элементы
Любые цифровые микросхемы строятся на основе простейших логических элементов "НЕ", "ИЛИ", "И".
Простейшим логическим элементом является инвертор, который работает в соответствии с таблицей, приведённой на рисунке 1. Этот логический элемент просто изменяет значение входного сигнала на прямо противоположное значение.
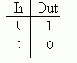
Рисунок 1. Таблица истинности логического инвертора
В качестве инвертора можно использовать обычный транзисторный усилитель с транзистором, включенном по схеме с общим эмиттером или истоком. Схемы, позволяющие реализовать функцию логического инвертирования, приведены на рисунке 2. На рисунке 2а приведена схема инвертора на обычном биполярном транзисторе, выполняющего функцию инвертирования, а на рисунке 2б приведена схема инвертора, выполненного на комплементарных МОП транзисторах.


Рисунок 2. Схемы, позволяющие реализовать функцию логического инвертирования.
Как видно из этих схем, функцию инвертирования осуществляет транзистор, включенный по схеме с общим эмиттером (общим истоком). Эти схемы обладают различным временем распространения сигнала и могут работать на различные виды нагрузки. Но независимо от схемы они осуществляют одну и ту же функцию. Для того, чтобы особенности включения транзисторов не затеняли выполняемую функцию, были введены специальные обозначения для цифровых микросхем.
Изображение инвертора на принципиальных схемах не зависит от технологии, по которой изготовлена цифровая микросхема, и приведено на рисунке 2.2. С этого момента схема инвертора в дальнейшем будет приводиться исключительно так, как это показано на рисунке 3.

Рисунок 3. Изображение логического инвертора на принципиальных схемах.
Часто
Следующим наиболее распространённым элементом в цифровой технике является элемент, реализующий логическую операцию "И", однако чаще всего существуют не отдельные схемы логического "И", а более сложные схемы, выполняющие одновременно логическую функцию "И" и логическую функцию "НЕ".
Таблица истинности схемы, выполняющей логическую функцию "2И-НЕ" приведена на рисунке 4.

Рисунок 4. Таблица истинности схемы, выполняющей логическую функцию "И-НЕ".
Как видно из приведённой таблицы истинности активный сигнал на выходе этого логического элемента появляется только тогда, когда и на входе X и на входе Y будут присутствовать логические единицы. То есть этот логический элемент действительно реализует операцию “И”
Проще всего построить такой элемент на самых обыкновенных ключах, как это показано на рисунке 5. В этой схеме ток будет протекать только тогда, когда оба ключа будут замкнуты, а значит, нулевой уровень на выходе схемы появится только при двух логических единицах на входе. Точно таким же образом выполняется элемент “И-НЕ” и на микросхемах, построенных по КМОП технологии, только в качестве ключа используется МОП транзистор. Схема логического элемента "И-НЕ", выполненного по КМОП технологии приведена на том же рисунке.


Рисунок 5. Принципиальные схемы, реализующие логическую функцию "2И-НЕ" Изображение схемы, выполняющей логическую функцию "2И-НЕ", на принципиальных схемах приведено на рисунке 6, и с этого момента схемы, выполняющие функцию “И” будут приводиться именно в таком виде. Это изображение не зависит от конкретного типа технологии построения цифровой микросхемы.

Точно также как не существует отдельных схем логического "И", выполненных по технологии ТТЛ, не существует отдельных схем логического "ИЛИ". Таблица истинности схемы, выполняющей логическую функцию "2ИЛИ-НЕ" приведена на рисунке 7.

Как и в предыдущем случае воспользуемся для реализации схемы “ИЛИ” ключами. На этот раз соединим ключи параллельно. Схема, реализующая таблицу истинности 7, приведена на рисунке 8. Схема логического элемента "2ИЛИ-НЕ", выполненного по КМОП технологии приведена на этом же рисунке.
Как видно из приведённых схем уровень логического нуля появится на выходе любой из этих схем, как только будет замкнут любой из ключей, то есть приведённые схемы реализуют таблицу истинности, приведённую на рисунке 7.


Так как одна и та же функция может быть реализована различными схемами, то для обозначения этой функции на принципиальных схемах используется специальный символ ‘1’, как это приведено на рисунке 9.

Рисунок 9. Изображение схемы, выполняющей логическую функцию "ИЛИ-НЕ".
[ ] [ ] [ ]
Малогабаритные лампочки накаливания
Наиболее простой схемой подключения к цифровым устройствам обладают лампочки накаливания. Эта схема приведена на рисунке 1.

В этой схеме потребовался транзистор, так как ток, протекающий через лампочку накаливания достаточно велик. Кроме того, такая схема включения позволяет использовать лампочки накаливания с напряжением питания, отличающимся от напряжения питания цифровых микросхем.
К сожалению эти индикаторы не отличаются надёжностью, так как при включении питания через них протекает значительный ток, в результате которого лампа может выйти из строя. Кроме того они боятся ударов. Все эти причины, а также большой потребляемый ток привели к тому, что в настоящее время эти индикаторы практически не используются.
Мультиплексоры
Мультиплексорами называются устройства, которые позволяют подключать несколько входов к одному выходу. Демультиплексорами называются устройства, которые позволяют подключать один вход к нескольким выходам. В простейшем случае такую коммутацию можно осуществить при помощи ключей:

Рисунок 1. Коммутатор (мультиплексор), собранный на ключах.
В цифровых схемах требуется управлять ключами при помощи логических уровней. То есть нужно подобрать устройство, которое могло бы выполнять функции электронного ключа с электронным управлением цифровым сигналом.
Рассмотрим таблицу истинности логического элемента "И". При этом один из входов логического элемента "И" будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента "И" эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y– информационным. Для простоты рассуждений, разделим таблицу истинности на две части в зависимости от уровня логического сигнала на управляющем входе X.

По таблице истинности отчетливо видно, что пока на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. То есть логический элемент "И" можно использовать в качестве электронного ключа. При этом не важно какой из входов элемента "И" будет использоваться в качестве управляющего входа, а какой - в качестве информационного. Остается только объединить выходы элементов "И" в один выход. Это делается при помощи элемента "ИЛИ" точно так же как и при построении схемы по произвольной таблице истинности. Такой вариант схемы коммутатора приведен на рисунке 2.

Рисунок 2. Принципиальная схема мультиплексора, выполненая на логических элементах.
В схемах, приведенных на рисунках 1 и 2, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный , как показано на рисунке 3. Это позволяет управлять переключением информационных входов при помощи двоичных кодов, подаваемых на управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.

Рисунок 3. Принципиальная схема мультиплексора, управляемого двоичным кодом.
Мультиплексор с двоичным управлением изображается на принципиальных схемах как показано на рисунке 4.

Рисунок 4. Обозначение мультиплексора на принципиальных схемах.
Мультивибраторы
Еще одной распространённой схемой генераторов на логических элементах является схема мультивибратора. В этой схеме для реализации положительной обратной связи используется два инвертора. Схема мультивибратора приведена на рисунке 5.

Рисунок 5. Схема мультивибратора, выполненная на двух логических инверторах.
В этой схеме возможна независимая регулировка частоты и скважности генерируемых колебаний. Длительность импульсов и длительность паузы между импульсами регулируется независимо при помощи RC цепочек R1 C2 и R3 C1. Если скважность генерируемых колебаний не важна, то можно упростить схему мультивибратора, использовав второй инвертор по прямому назначению. В этом случае схема мультивибратора примет вид, показанный на рисунке 6.

Рисунок 6. Упрощённая схема мультивибратора.
В этой схеме возможно задавать только частоту генерируемых импульсов. Эта частота будет определяться произведением R1 C1. Скважность генерируемых импульсов будет зависеть только от соотношения токов нуля и единицы выбранного логического элемента.
Достаточно часто требуется возможность получить генератор, выходная частота которого могла бы изменяться в достаточно широких пределах. В этом случае в качестве частотозадающего элемента в генераторе может быть использован элемент с изменяемыми параметрами, например варикап или полевой транзистор. Схема такого генератора, управляемого напряжением, приведена на рисунке 7.

Рисунок 7. Схема генератора, управляемого напряжением.
Учитывая, что сопротивление полевого транзистора может изменяться в пределах от 10 Ом до 10 МОм, генерируемая частота тоже может изменяться в десятки и сотни раз. Однако следует учесть, что такой генератор может быть использован только в цифровых схемах, так как его спектральные характеристики оставляют желать лучшего. Обычно такая схема используется в цепях умножения частоты внутри цифровых микросхем повышенной производительности. Примером специализированных микросхем - генераторов могут служить микросхемы 531ГГ1 и 564ГГ1.
В схеме на мультивибраторе можно использовать и кварцевую стабилизацию частоты. Для этого нужно кварцевый резонатор включить в цепь обратной связи. Схема мультивибратора с кварцевой стабилизацией частоты приведена на рисунке 8.

Рисунок 8. Схема мультивибратора с кварцевой стабилизацией частоты.
[ ] [ ] [ ]
Недвоичные счётчики с обратной связью
Если посмотреть на временную диаграмму сигналов на выходах двоичного счётчика, приведённого на рисунке 1, то можно увидеть, что частота сигналов на его выходах будет уменьшаться в два раза по отношению к предыдущему выходу. Это позволяет использовать счетчики в качестве делителей частоты входного сигнала. Эти делители частоты могут быть использованы в устройствах формирования высокостабильных генераторов частоты (синтезаторов частот). Частоты могут быть использованы либо для синхронизации цифровых устройств (в том числе и микропроцессоров) либо в качестве задающих генераторов радиоприёмных и радиопередающих устройств.

Рисунок 1. Временная диаграмма четырёхразрядного счётчика.
При использовании цифровых счётчиков в качестве устройств формирования опорных частот может потребоваться обеспечить коэффициент деления, отличающийся от степени числа 2. Ещё одна ситуация, когда необходимо применять недвоичные счётчики возникает при отображении информации, записанной в счётчике. Человек, который работает с электронной техникой, привык работать с десятичной системой счисления, поэтому возникает необходимость отображать хранящееся в счётчике число в непосредственно десятичном виде. Это намного проще сделать, если и счет вести сразу в коде. Иначе для индикации потребуется перекодировать информацию из в код.
Построить недвоичный счётчик можно из двоичного за счёт выбрасывания лишних комбинаций единиц и нулей. Это может быть осуществлено при помощи обратной связи. Для этого при помощи определяется число, соответствующее коэффициенту счёта, и сигнал с выхода этого дешифратора обнуляет содержимое двоичного счётчика. В качестве примера на рисунке 2 приведена схема двоично-десятичного счётчика.

Рисунок 2 Схема десятичного счётчика, построенного на основе двоичного счётчика.
В этой схеме дешифратор построен на двухвходовой схеме "2И", входящей в состав микросхемы двоичного счётчика. Дешифратор декодирует число 10 (1010 в двоичной системе счисления). В соответствии с принципами построения схем по произвольной таблице истинности для построения дешифратора требуется ещё два инвертора, подключённых к выходам 1 и 4.
Однако после сброса счётчика числа, большие 10 никогда не смогут появиться на выходах микросхемы. Поэтому схема дешифратора упрощается и вместо четырёхвходовой схемы "4И" можно обойтись двухвходовой схемой. Инверторы тоже оказываются лишними.
При использовании счётчиков в качестве делителей частоты тоже можно воспользоваться обратной связью. Приведём в качестве примера схему делителя частоты на 1000. При разработке делителя прежде всего определим сколько потребуется микросхем двоичных счётчиков. Для этого определим степень числа 2, при которой число M=2n будет больше требуемого числа 1000. Это будет число 10. При возведении основания системы счисления 2 в 10 степень получится число 1024. То есть, при использовании для построения делителя частоты непосредственно триггеров, достаточно будет десяти триггеров. Однако обычно для построения делителей частоты используют готовые двоичные счётчики, поэтому определим необходимое количество микросхем двоичных счётчиков. При использовании четырёхразрядных двоичных счётчиков достаточно будет трёх микросхем, так как в трёх микросхемах будет 3*4=12 триггеров, что заведомо больше минимального числа триггеров.
Следующим этапом построения делителя частоты будет перевод коэффициента деления 1000 в двоичное представление. Десятичное число 1000 в двоичном виде будет выглядеть как 0011 1110 1000. В этом числе шесть единиц, поэтому для построения делителя будет достаточно шестивходовой схемы "И". Однако такие схемы не выпускаются, поэтому воспользуемся микросхемой "8И-НЕ". Неиспользуемые входы этой микросхемы подключим к питанию. Ненужную нам инверсию сигнала скомпенсируем дополнительным инвертором. Получившаяся схема делителя на 1000 приведена на рисунке 3.

Рисунок 3 Схема делителя на 1000, построенного на основе трёх двоичных счётчиков.
При использовании счётчиков в составе синтезаторов частот может потребоваться формирование целого диапазона частот. В этом случае делитель должен обладать возможностью изменения коэффициента деления (ДПКД).При использовании обратной связи для этого потребуется полный дешифратор и переключатели его выходов на вход сброса счётчика. Схема при этом получается сложной, а управление неудобным. Пример двухразрядного делителя с переменным коэффициентом деления (ДПКД), построенного на десятичных счётчиках приведён на рисунке 4.

Рисунок 4. Схема делителя с переменным коэффициентом деления с максимальным коэффициентом деления 100, построенного на основе двух десятичных счётчиков.
[ ] [ ] [ ]
Недвоичные счётчики с предварительной записью
В счётчиках с обратной связью исключаются последние состояния двоичного счётчика. Можно поступить по другому. Начать с последнего состояния счётчика и воспользовавшись вычитающим счётчиком определять нулевое состояние счётчика. Это состояние очень просто можно определить при помощи схемы "И". В таком случае необходимо иметь возможность предварительной записи в счётчик. То есть счётчик при предварительной записи должен вести себя как
[ ] [ ] [ ]
Области применения цифровых микросхем
Цифровые микросхемы первоначально разрабатывались для построения электронно-вычислительных машин, получивших в дальнейшем название компьютеры. То есть первое их предназначение было заменить человека при выполнении рутинной работы. Сейчас, наверное, никто и не вспомнит, что слово калькулятор ещё каких-нибудь шестьдесят лет назад обозначало не маленький карманный прибор, а профессию большого числа людей, которые занимались расчётами по конкретным математическим формулам.
Однако вскоре после начала массового производства цифровых микросхем выяснилось, что они оказались очень удобны для управления какими либо объектами. При этом управляемая схема может обычно находиться в двух состояниях. Например: схема может быть либо включена, либо выключена, светодиод может либо гореть, либо не гореть, соединение в телефонной станции может быть или не быть, радиостанция может находиться в режиме передачи или в режиме приёма. В результате цифровые микросхемы практически полностью вытеснили применявшиеся ещё с девятнадцатого века для управления приборами электромагнитные реле и перфокарты.
При выполнении задачи управления для описания состояния объекта достаточно двух значений: напряжение высокое или низкое (положительное или отрицательное) ток протекает или не протекает. Это позволило избавиться от многих неприятных моментов аналоговых схем. Например, ошибка при прохождении через схему не увеличивается (в отличие от шумов), а в ряде случаев даже может быть скомпенсирована. Сами цифровые схемы при правильном использовании не вносят ошибок. Эти свойства цифровых микросхем привели к бурному развитию цифровой техники.
Приведённые преимущества привели к тому, что в дальнейшем цифровая техника стала использоваться и для решения других задач. Например для формирования высокостабильных колебаний для радиотехнических изделий или для использования в часах. Здесь тоже нет необходимости формировать различные уровни напряжения генерируемого сигнала. Достаточно только, чтобы частота генерируемого колебания была стабильной.
Затем стали разрабатываться методы и теория применения цифровых микросхем для формирования аналоговых сигналов. И здесь тоже основным фактором была возможность заранее прогнозировать уровень шумов. При этом уровень шума зависит только от сложности схемы, и не зависит (ну, или почти не зависит) от количества схем, через которые проходит сигнал. Это приводит к возможности передавать сигнал на любое расстояние (или производить любое количество копий сигнала).
Особенности кварцевой стабилизации частоты генераторов
При разработке кварцевого генератора следует обращать внимание, что кварцевый генератор на основе работает несколько по другим принципам по сравнению с схемой. Если в осцилляторной схеме кварцевый резонатор используется в качестве индуктивности, входящей в колебательный контур резонатора, то в схеме мультивибратора кварцевый резонатор используется в качестве узкополосного фильтра в цепи обратной связи. Это приводит к тому, что один и тот же резонатор, включённый в схему мультивибратора и осцилляторную схему, будет генерировать различные частоты!
Для того, чтобы разобраться с этим явлением, вспомним эквивалентную схему кварцевого резонатора и характеристику зависимости сопротивления кварцевого резонатора от частоты. Эквивалентная схема кварцевого резонатора приведена на рисунке 9 а, а характеристика зависимости сопротивления от частоты - на рисунке 9 б.


Рисунок 9. а - эквивалентная схема кварцевого резонатора;
б - зависимость сопротивления кварцевого резонатора от частоты.
В схеме мультивибратора используется последовательный резонанс кварцевого резонатора (собственные колебания кристалла), а в схеме генерация производится на частоте, близкой к параллельному резонансу контура, образуемого индуктивностью резонатора и ёмкостью кварцедержателя. Эти частоты близки, но не могут совпадать по определению. В результате частоты генерируемых колебаний будут отличаться между собой. Обычно разность частот последовательного и параллельного резонансов составляет около 1 килогерца. Настолько же будут отличаться и частоты кварцевых генераторов, построенных по схеме и схеме ёмкостной трёхточки.
Так как генератор, собранный по схеме мультивибратора возбуждается на собственной частоте кварцевого кристалла, то стабильность кварцевого мультивибратора будет выше по сравнению с осцилляторной схемой, так как на частоту последовательного резонанса кварцевого резонатора не влияют внешние паразитные ёмкости. Однако в этой схеме возможно самовозбуждение генератора на частоте, далеко отстоящей от резонансной частоты кварцевого резонатора. Это обуславливается ёмкостью кварцедержателя, поэтому в схеме мультивибратора необходимо предусматривать специальные меры для борьбы с этим явлением.
При построении схем генераторов следует отметить, что они являются мощными источниками помех, поэтому эти генераторы обычно экранируют. Цепи питания микросхем, на которых реализуются генераторы обязательно содержат фильтрующие высокочастотные конденсаторы. Часто для лучшей фильтрации по цепи питания кроме конденсаторов используются фильтрующие дроссели.
Для уменьшения помех используются и конструктивные меры. Например, рядом с цепью генерируемого сигнала прокладывают корпусные проводники. Таким образом фактически образуется полосковая (или волноводная) линия передачи.
[ ] [ ] [ ]
Построение произвольной таблицы истинности
Любая логическая схема без памяти полностью описывается таблицей истинности. При построении сложных логических схем с произвольной таблицей истинности используется сочетание простейших схем "И" "ИЛИ" "НЕ".
При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) отдельно. Для реализации схемы можно воспользоваться как схемами “И” так и схемами “ИЛИ”. В настоящее время наиболее распространены микросхемы, совместимые с ТТЛ технологией, а в этой технологии проще всего получить элементы “И”. Поэтому рассмотрим способ реализации произвольной таблицы истинности основанный на логических элементах “И”.
Для реализации таблицы истинности при помощи логических элементов "И" достаточно рассмотреть только те строки таблицы истинности, которые содержат логические "1" в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую "1", реализуется схемой логического "И" с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.
Входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим нулем, подаются на вход этой же схемы "И" через инверторы. Объединение сигналов с выходов схем "И", реализующих отдельные строки таблицы истинности, производится при помощи схемы логического “ИЛИ”. Количество входов в схеме “ИЛИ” определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 10:

Рисунок 10. Произвольная таблица истинности.
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные красным цветом. Эти строки реализуются микросхемой D2 на рисунке 11.
Каждая строка реализуется своей схемой "И", затем выходы этих схем объединяются. Количество входов элемента “И” однозначно определяется количеством входных сигналов в таблице истинности. Количество этих элементов, а значит и количество входов в логическом элементе “ИЛИ” определяется количеством строк с единичным сигналом на реализуемом выходе схемы.
Для построения схемы, реализующей сигнал Out2, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше, и поэтому повторяться не будет.

Рисунок 11. Принципиальная схема, реализующая таблицу истинности, приведенную на рисунке 10.
Обычно при построении цифровых схем после реализации таблицы истинности производится минимизация схемы, но для упрощения понимания материала минимизация производиться не будет. Это оправдано еще и с той точки зрения, что неминимизированные схемы обычно обладают максимальным быстродействием.
[ ] [ ]
Регистры
Регистром называется последовательное или параллельное соединение триггеров. Регистры обычно строятся на основе D триггеров. При этом для построения регистров могут использоваться как универсальные D триггеры, так и триггеры-защелки. При использовании для построения параллельного регистра триггеров-защелок регистр называется регистр-защелка. Параллельный регистр служит для запоминания многоразрядного двоичного слова. Количество триггеров, входящее в состав параллельного регистра определяет его разрядность. Схема четырёхразрядного параллельного регистра приведена на рисунке 1, а его обозначение на принципиальных схемах на рисунке 2.

Рисунок 1. Схема параллельного регистра.

Рисунок 2. Обозначение параллельного регистра на принципиальных схемах.
При записи информации в параллельный регистр все биты (двоичные разряды) записываются одновременно.
Последовательный регистр (регистр сдвига) обычно служит для преобразования последовательного кода в параллельный и наоборот. Схема регистра, осуществляющего преобразование последовательного кода в параллельный, приведена на рисунке 3, а его изображение на принципиальных схемах - на рисунке 4.

Рисунок 3. Схема последовательного регистра.

Рисунок 4. Обозначение последовательного регистра на принципиальных схемах.
Регистры сдвига выполняют обычно как универсальные последовательно-параллельные микросхемы. Переключение регистра из параллельного режима в последовательный и наоборот осуществляется при помощи мультиплексора. Схема такого регистра приведена на рисунке 5, а его изображение на принципиальных схемах - на рисунке 6.

Рисунок 5. Схема универсального регистра.

Рисунок 6. Обозначение универсального регистра на принципиальных схемах.
[ ] [ ] [ ]
Счётчики
Счётчики используются для построения или для выборки инструкций из ПЗУ в микропроцессорах. Они могут использоваться как делители частоты в управляемых генераторах частоты (синтезаторах). При использовании в цепи ФАП счётчики могут быть использованы для умножения частоты как в синтезаторах, так и в микропроцессорах.
Синхронные счётчики
В рассмотренных схемах счётчиков быстродействие всего счётчика определяется временем распространения сигнала от входа до выхода самого старшего разряда. При этом получается, что чем больше коэффициент счёта, тем больше двоичных разрядов счётчика требуется для реализации этого счётчика, тем большее время требуется для распространения сигнала от входа синхронизации счётчика, до его выхода, и тем меньше будет предельная частота, которую можно подавать на вход этого счётчика.
[ ] [ ] [ ]
Сумматоры
Построение двоичных сумматоров обычно начинается с сумматора по модулю 2. На рисунке 1 приведена таблица истинности этого сумматора. Ее можно получить исходя из правил суммирования в двоичной арифметике. Предполагается, что читатель знаком с основами двоичной арифметики. Более подробно операции над двоичными числами будут рассмотрены позднее.

Рисунок 1. Таблица истинности сумматора по модулю 2.
В соответствии с принципами , рассмотренными в предыдущей главе, получим схему сумматора по модулю 2. Эта схема приведена на рисунке 2.

Рисунок 2. Принципиальная схема, реализующая таблицу истинности сумматора по модулю 2.
Сумматор по модулю 2 (для двоичной арифметики его схема совпадает со схемой исключающего "ИЛИ") изображается на схемах как показано на рисунке 3.

Рисунок 3. Изображение схемы, выполняющей логическую функцию исключающего "ИЛИ".
Сумматор по модулю 2 выполняет суммирование без учета переноса. В полном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена на рисунке 4.

Рисунок 4. Таблица истинности полусумматора.
В соответствии с получим схему полусумматора. Эта схема приведена на рисунке 5.

Рисунок 5. Принципиальная схема, реализующая таблицу истинности полусумматора.
Полусумматор изображается на схемах как показано на рисунке 6.

Рисунок 6. Изображение полусумматора на схемах.
Схема полусумматора формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому она и называется полусумматором. Таблицу истинности полного двоичного одноразрядного сумматора можно получить из правил суммирования двоичных чисел. Она приведена на рисунке 7. В обозначении входов использовано следующее правило: в качестве входов использованы одноразрядные числа A и B; перенос обозначен буквой P; для обозначения входа переноса используется буква I (сокращение от английского слова input – вход); для обозначения выхода переноса используется буква O (сокращение от английского слова output – выход).

Рисунок 7. Таблица истинности полного двоичного одноразрядного сумматора.
В соответствии с получим схему полного двоичного одноразрядного сумматора. Эта схема приведена на рисунке 8. Ее можно минимизировать, но это несколько усложняет принципы построения сумматоров, поэтому вопросы минимизации рассматриваться не будут.

Рисунок 8. Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора.
Полный двоичный одноразрядный сумматор изображается на схемах как показано на рисунке 9.

Рисунок 9 Изображение полного двоичного одноразрядного сумматора на схемах.
Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов. Схема соединения одноразрядных сумматоров для реализации четырехразрядного сумматора приведена на рисунке 10.

Рисунок 10. Принципиальная схема многоразрядного двоичного сумматора.
Одноразрядные сумматоры практически никогда не использовались, так как почти сразу же были выпущены микросхемы многоразрядных сумматоров. Полный двоичный четырехразрядный сумматор изображается на схемах как показано на рисунке 11.

Рисунок 11. Изображение полного двоичного многоразрядного сумматора на схемах.
Естественно, в приведенной на рисунке 10 схеме рассматриваются только принципы работы двоичных сумматоров. В реальных схемах никогда не допускают последовательного распространения переноса через все разряды многоразрядного сумматора. Для увеличения скорости работы двоичного сумматора применяется отдельная схема формирования переносов для каждого двоичного разряда. Таблицу истинности для такой схемы легко получить из алгоритма суммирования двоичных чисел, а затем применить хорошо известные нам принципы построения цифровой схемы по произвольной таблице истинности.
На этом пока закончим рассмотрение принципов работы сумматора, более сложные операции будут рассмотрены позднее, а пока для дальнейшего понимания работы операционного блока процессора необходимо научиться переключать двоичные числа на входах и выходе сумматора.Это позволяют сделать и , основной частью которых является дешифратор, поэтому следующим устройством, которое мы рассмотрим, будет декодер. Дешифратор является частным случаем декодера.
[ ]
Технологии производства цифровых микросхем
В настоящее время используется несколько технологий построения логических элементов:
транзисторно-транзисторная логика (ТТЛ, TTL) логика на основе комплементарных МОП транзисторов (КМОП, CMOS) логика на основе сочетания комплементарных МОП и биполярных транзисторов (BiCMOS)Первоначально получили распространение цифровые микросхемы, построенные на основе ТТЛ технологии. Поэтому до сих пор существует огромное количество микросхем, построенных по этой технологии или совместимые с этими микросхемами по напряжению питания, логическим уровням и цоколёвке.
Рассмотрим сначала микросхемы, совместимые с первыми ТТЛ микросхемами по питанию. Это микросхемы, питающиеся от источника напряжения +5В. Зарубежные ТТЛ микросхемы получили название серия SN74. Конкретные микросхемы этой серии обозначаются цифровым номером микросхемы, следующим за названием серии. Принципиальная схема типового элемента ТТЛ микросхемы приведена на рисунке 1.
Рисунок 1. Принципиальная схема типового элемента ТТЛ микросхемы.
Отечественные микросхемы этой серии выпускались в составе серий К134 (низкое быстродействие низкое потребление)
[ ] [ ]
Триггеры
Триггеры предназначены для запоминания двоичной информации. Использование триггеров позволяет реализовывать устройства оперативной памяти (то есть памяти, информация в которой хранится только на время вычислений). Однако триггеры могут использоваться и для построения некоторых цифровых устройств с памятью, таких как , или цифровые линии задержки.
Простейшая схема, позволяющая запоминать двоичную информацию, строится на основе простейших логических элементов, "ИЛИ" или "И". Такая схема, построенная на элементах "И" приведена на рисунке 1. Вход S (Set) позволяет устанавливать выход триггера Q в единичное состояние при подаче на его вход логического нуля. Вход R (Reset) позволяет сбрасывать выход триггера Q в нулевое состояние при подаче на его вход логического нуля. По названию своих входов и сам триггер получил название RS-триггера.

Рисунок 1 Схема простейшего триггера на схемах "И". Входы R и S инверсные (активный уровень'0')
Точно так же можно построить RS-триггер и на логических элементах "ИЛИ". Схема RS триггера, построенного на логических элементах "ИЛИ" приведена на рисунке 2. Единственное отличие будет заключаться в том, что сброс и установка триггера будет производиться единичными логическими уровнями.

Рисунок 2 Схема простейшего триггера на схемах "ИЛИ". Входы R и S прямые (активный уровень '1')
Так как триггер при построении его на различных элементах работает одинаково, то его изображение на принципиальных схемах тоже одинаково. Изображение простейшего триггера на принципиальных схемах приведено на рисунке 3.

Рисунок 3 Обозначение простейшего триггера на принципиальных схемах
Схема триггера позволяет запоминать состояние логической схемы, но так как в начальный момент времени может возникать переходный процесс (в цифровых схемах этот процесс называется опасные гонки), то запоминать состояния логической схемы нужно только в определённые моменты времени, когда все переходные процессы закончены.
То есть цифровые схемы требуют синхросигнала. Все переходные процессы должны закончиться за время периода синхросигнала.
Для таких цифровых схем требуются синхронные триггеры. Схема синхронного триггера приведена на рисунке 4, а обозначение на принципиальных схемах на рисунке 5.

Рисунок 4 Схема синхронного триггера на схемах "И"

Рисунок 5 Обозначение синхронного триггера на принципиальных схемах
В приведенной схеме для записи логического 0 и логической 1 требуются разные входы, что не всегда удобно. Поэтому для запоминания дискретной информации применяются D триггеры. Схема такого триггера приведена на рисунке 6, а обозначение на принципиальных схемах на рисунке 7.

Рисунок 6 Схема D триггера (защелки)

Рисунок 7 Обозначение D триггера (защелки) на принципиальных схемах
Во всех приведенных схемах синхросигнал работает по уровню, поэтому триггеры называются триггеры-защёлки. Легче всего объяснить появление этого названия по временной диаграмме, приведенной на рисунке 8.

Рисунок 8. Временная диаграмма D триггера (защелки)
По этой временной диаграмме видно, что триггер-защелка хранит данные на выходе только при нулевом уровне на входе синхронизации. Если же на вход синхронизации подать активный высокий уровень, то напряжение на выходе триггера будет повторять напряжение, подаваемое на вход этого триггера. Входное напряжение запоминается только в момент изменения уровня напряжения на входе синхронизации C с высокого уровня на низкий уровень. Входные данные как бы "защелкиваются" в этот момент. отсюда и название - триггер-защелка.
Принципиально в этой схеме входной переходной процесс может беспрепятственно проходить на выход триггера. Поэтому там, где это важно, необходимо сокращать длительность импульса синхронизации до минимума. Чтобы преодолеть такое ограничение были разработаны триггеры, работающие по фронту. Схема такого триггера приведена на рисунке 9, а обозначение на принципиальных схемах на рисунке 10.

Рисунок 9 Схема универсального D триггера

Рисунок 10 Обозначение универсального D триггера на принципиальных схемах
[ ] [ ] [ ]
Для желающих читается курс цифровая обработка сигналов
Курс цифровая обработка сигналов предполагает углублённое изучение вопросов цифровой обработки сигналов. Рассматриваются особенности выбора частоты преобразования и обработки сигналов, особенности подключения АЦП к сигнальным процессорам, особенности построения аналоговых формирующих фильтров, принципы реализации элементов цифровой обработки сигналов на микроконтроллерах.
Занятия начинаются по мере формирования групп. Количество человек в группе - 12 человек. Для записи обращаться: Главный корпус СибГУТИ каф. САПР к 302 (3 этаж) тел. для справок: 66-02-86.
Фильтры для устранения эффекта наложения спектров (Антиалайзинговые фильтры)
Говоря о дискретизации низкочастотного сигнала (огибающей сигнала или видеосигнале) подразумевают, что подлежащий дискретизации сигнал лежит в первой зоне Найквиста. Важно обратить внимание на то, что без фильтрации на входе идеального дискретизатора любой частотный компонент (сигнал или шум), который находится за пределами "полосы Найквиста", в любой зоне Найквиста будет создавать НЧ- образ в первой зоне Найквиста. Поэтому на входе АЦП для подавления мешающих сигналов используется ФНЧ.
Важно правильно определить характеристики ограничивающего спектр фильтра. Первым шагом является получение характеристик сигнала, подлежащего дискретизации. Предположим что, когда наивысшая из интересующих нас частот равна fa. Тогда фильтр должен пропускать сигналы, лежащие в полосе частот от 0 до fa, и подавлять сигналы с частотой выше fa.
Предположим, что частота среза фильтра равна fa. На рисунке 1а показан эффект возникновения помехи, обусловленной отображением сигнала из второй зоны Найквиста в первую. Именно эта помеха определяет динамический диапазон системы DR. В приведённом примере составляющие спектра, которые попадают в диапазон между fa и fs /2, не представляют интереса и не ограничивают динамический диапазон системы. Необходимо отметить, что в ряде источников этот эффект называется эффектом "заворота спектра".

Рисунок 1 Влияние частоты дискретизации на требования к аналоговому фильтру.
Таким образом крутизна АЧХ определяется верхней частотой сигнала fa, началом полосы задерживания fs-fa и требуемым затуханием в полосе задерживания DR. Динамический диапазон системы выбирается исходя из требований точности представления сигнала.
При всех прочих равных условиях фильтры становятся более сложными по мере того, как увеличивается крутизна АЧХ. Например, фильтр Баттерворта дает ослабление 6 дБ на октаву для каждого порядка. Для достижения ослабления 60 дБ на частоте 2 МГц при полосе сигнала 1 МГц (1 октава) требуется как минимум фильтр 10-го порядка - это фильтр, весьма трудный в разработке и дорогой в производстве.

Рисунок 2 АЧХ фильтра Баттерворта 10-го порядка.
Кроме сложности разработки и производства фильтры высокого порядка обладают ещё рядом недостатков, таких как нелинейная фазовая характеристика и увеличение групповой задержки на краю полосы пропускания фильтра. В качестве примера на рисунке 2 приведена амплитудно-частотная характеристика фильтра Баттерворта 10-го порядка, а на рисунке 3 - фазо-частотная характеристика и зависимость группового времени запаздывания от частоты. Всё это приводит к тому, что при преобразовании сигнала из аналоговой формы в цифровую нежелательно использовать аналоговые фильтры формирования спектра высокого порядка.
 |
 |
Из приведённых рассуждений видно, что недостаточная крутизна спада ФНЧ может компенсироваться более высокой частотой дискретизации АЦП. Выбрав более высокую частоту дискретизации (избыточную дискретизацию), мы уменьшаем требование к крутизне спада и, следовательно, сложность фильтра. Этот эффект достигается за счет использования более быстрого АЦП и более высокой скорости обработки данных. На рисунке 1б показан эффект, возникающий при увеличении частоты дискретизации в K раз, при неизменных требованиях к частоте среза fa и к динамическому диапазону DR. Более пологий скат делает этот фильтр проще для проектирования, по сравнению со случаем, показанным на рисунке 1а.
ИЗБЫТОЧНАЯ ДИСКРЕТИЗАЦИЯ УМЕНЬШАЕТ ТРЕБОВАНИЯ К КРУТИЗНЕ СПАДА ФНЧ
Процесс проектирования аналогового фильтра начинается с выбора начальной частоты дискретизации. Она обычно выбирается в диапазоне от 2,5 fa до 4 fa. Затем, исходя из требуемого динамического диапазона, определяется характеристика фильтра, и определяется реализуемость такого фильтра с учетом ограничений по стоимости системы и требуемой производительности этой системы. Если реализация окажется невозможной, полезно рассмотреть вариант с более высокой частотой дискретизации, для которого, возможно, потребуется более быстрый АЦП.
Следует отметить, что sigma-delta-АЦП изначально являются преобразователями с избыточной дискретизацией, и данное обстоятельство существенно ослабляет требования к аналоговому фильтру, формирующему спектр, что является дополнительным преимуществом данной архитектуры.
Требования к аналоговому формирующему спектр фильтру могут быть несколько ослаблены, если вы уверены, что сигнал с частотой, которая попадает в полосу задержки fs - fa, никогда не достигнет амплитуды основного сигнала. Во многих приложениях появление таких сигналов на этой частоте действительно маловероятно. Если максимум сигнала в полосе частот fs - fa никогда не превысит X дБ над амплитудой основного сигнала, то требования к затуханию в полосе задержки фильтра может быть уменьшено на ту же самую величину. Новое требование к затуханию в полосе задержки fs - fa основано на понимании того факта, что в этом случае значение подавляемого сигнала составляет DR-X дБ. В случае реализации этого варианта будьте внимательны при устранении любых шумов, частоты которых могут быть выше частоты fa - это мешающие сигналы, которые также будут создавать НЧ- составляющую в полосе сигнала.
Искажения и шум в идеальном N-разрядном АЦП
До сих пор мы анализировали процесс дискретизации без рассмотрения такой операции АЦП, как квантование. Теперь будем трактовать АЦП как идеальный дискретизатор, но учитывать при этом эффекты квантования.
Идеальный N-разрядный АЦП имеет погрешности (по постоянному или переменному току), связанные только с процессами дискретизации и квантования. Максимальная погрешность, которую имеет идеальный АЦП при оцифровывании входного сигнала, равна ±1/2 LSB. Любой аналоговый сигнал, поступающий на вход идеального N- разрядного АЦП, производит шум квантования. Среднеквадратичное значение шума (измеренное по ширине полосы Найквиста, от постоянного тока до fs/2) приблизительно равно весу наименьшего значащего разряда (LSB) q, деленному на v12. (см. Приложение 2). При этом предполагается, что амплитуда сигнала составляет, по крайней мере, несколько младших разрядов, так что выход АЦП изменяет свое состояние почти при каждом отсчете. Сигнал ошибки квантования от входного линейного пилообразного сигнала аппроксимируется сигналом пилообразной формы с максимальным размахом q, и его среднеквадратичное значение равно q/v12 (см. рис.2.15).
Можно показать, что отношение среднеквадратичного значения синусоидального сигнала, соответствующего полной шкале, к среднеквадратичному значению шума квантования (выраженное в дБ) равно:

где N - число разрядов в идеальном АЦП. Это уравнение имеет силу только в том случае, если шум измерен на полной ширине полосы Найквиста от 0 до fs /2, как показано на рис.2.16. Если ширина полосы сигнала BW меньше fs /2, то значение отношения сигнал/шум (SNR) в пределах ширины полосы сигнала BW возрастет вследствие уменьшения энергии шума квантования в пределах ширины полосы. Для этого условия правильным будет следующее выражение:


Рис. 2.15 Шум квантования идеального N-разрядного АЦП

Рис. 2.16 Спектр шума квантования
Приведенное уравнение отражает состояние, именуемое избыточной дискретизацией, при котором частота дискретизации выше, удвоенной ширины полосы сигнала.
Корректирующую величину часто называют запасом по дискретизации. Обратите внимание, что для заданной ширины полосы сигнала удвоение частоты дискретизации увеличивает отношение сигнал/шум на 3 дБ.
Хотя среднеквадратичное значение шума точно описывается формулой

В большинстве устройств входной сигнал АЦП (он обычно смешан с некоторым шумом) представляет собой полосу частот со случайным шумом квантования. Тем не менее, в устройствах спектрального анализа (или при выполнении БПФ на АЦП, использующих спектрально чистый синусоидальный сигнал, см. рис.2.17) корреляция между шумом квантования и сигналом зависит от отношения частоты дискретизации к частоте входного сигнала. Это демонстрируется на рис.2.18, где идеальный выход 12-разрядного АЦП представлен с использованием БПФ с 4096 точками. На левом графике отношение частоты дискретизации к входной частоте было выбрано равным точно 32, и худшая гармоника составляет 76 дБ от основной частоты. Правый график показывает эффект некоторого смещенного отношения, приводящего к относительному разбросу спектра случайного шума, благодаря которому динамический диапазон, свободный от гармоник (SFDR), достигает 92 дБ. В обоих случаях среднеквадратичное значение всех шумовых компонентов равно q/v12, но в первом случае шум сконцентрирован около гармоник основной частоты.



Рис. 2.18 Влияние отношения частоты дискретизации к входной частоте на динамический диапазон (SFDR) для идеального АЦП
Обратите внимание, что это изменение нелинейных искажений АЦП является следствием процесса дискретизации и корреляции ошибки квантования с входной частотой. В практике аналого-цифрового преобразования ошибка квантования вообще проявляется как случайный шум из-за случайной природы широкополосного входного сигнала и того факта, что обычно имеется небольшой шум системы, который действует, как подмешиваемый псевдослучайный сигнал при дальнейшем распределении спектра ошибки квантования.
Отмеченное очень важно, потому что для определения характеристик АЦП часто используется быстрое преобразование Фурье (БПФ) для монотонного синусоидального сигнала. Для точного измерения нелинейных искажений АЦП должны быть предприняты шаги, гарантирующие, что испытательная установка верно измеряет искажения, идущие от АЦП, с учетом эффекта корреляции шума квантования. Это достигается соответствующим выбором соотношения испытательных частот и частот дискретизации, а иногда – добавлением к входному сигналу некоторого шума (псевдослучайного сигнала).
Вернувшись к рис.2.18, обратите внимание, что минимальный уровень шума, полученного с помощью БПФ, приблизительно равен 100 дБ от полной шкалы АЦП, тогда как т еоретическое отношение сигнал/шум 12-разрядного АЦП равно 74 дБ. Минимальный уровень шума от БПФ не равен отношению сигнал/шум АЦП, потому что БПФ действует, подобно аналоговому анализатору спектра с шириной полосы fs /M, где М – число точек БПФ. Теоретически минимальный уровень шума БПФ равен 10 log10 (M/2) дБ, то есть ниже минимального уровня шума квантования из-за так называемого выигрыша БПФ в отношении сигнал/шум (см. рис.2.19). В случае идеального 12-разрядного АЦП с отношением сигнал/шум 74 дБ, использование БПФ с 4096 точками привело бы к выигрышу в отношении сигнал/шум в 10 log10 (4096/2) = 33 дБ, приводя, таким образом, к предельному отношению сигнал/шум 74+33=107 дБ. В действительности, минимальный уровень шума БПФ может быть еще уменьшен за счет увеличения количества точек БПФ, подобно тому, как минимальный уровень шума аналогового анализатора спектра может быть уменьшен за счет сужения ширины полосы пропускания.
При испытаниях АЦП, использующих БПФ, важно быть уверенным, что количество точек БПФ достаточно велико для того, чтобы нелинейные искажения можно было отличить от минимального уровня ума БПФ.
Рис. 2.19 Уровень шума идеального 12-разрядного АЦП при 4096-точечном БПФ
Искажение и шум в реальных АЦП
На практике дискретизация сигнала в АЦП (с интегрированным устройством выборки- хранения УВХ), независимо от архитектуры, проходит при наличии шумов и искажений сигнала, как это показано на рис.2.20. Широкополосному аналоговому входному буферу присущи широкополосный шум, нелинейность и конечная ширина полосы. УВХ (SHA) вносит дальнейшую нелинейность, ограничение полосы и дрожание апертуры. Квантующая часть АЦП вносит шум квантования, интегральную и дифференциальную нелинейности. В этом обсуждении предполагается, что сигналы с последовательных выходов АЦП загружаются в буферную память длиной М и что БПФ процессор имеет спектральный выход. Также допускается, что арифметические операции БПФ не вносят никаких существенных погрешностей в АЦП. Однако при проверке минимального выходного уровня шума должен быть рассмотрен выигрыш в отношении сигнал/шум БПФ (зависящий от M).
МОДЕЛЬ АЦП, ПОКАЗЫВАЮЩАЯ ИСТОЧНИКИ
ШУМОВ И ИСКАЖЕНИЙ СИГНАЛА
Рис. 2.20
Приведенный ко входу тепловой шум
Широкополосные внутренние цепи АЦП вносят некоторое среднеквадратичное значение широкополосного шума из-за воздействия тепла и дисперсии шума kT/C. Этот шум присутствует даже для сигналов постоянного тока и объясняет тот факт, что результатом работы большинства широкополосных (с высокой разрешающей способностью) АЦП является распределение кодов, сконцентрированное вокруг номинального значения входного сигнала (см. рис.2.21). Чтобы измерить его значение, вход АЦП заземляется, накапливается большое количество выходных отсчетов и составляется график в виде гистограммы (иногда упоминаемый как гистограмма с заземленным входом). Так как шум имеет почти Гауссово распределение, стандартное отклонение гистограммы легко рассчитывается (см.
Приложение 3) в соответствии с эффективным среднеквадратичным значением входного шума. Обычной практикой для выражения среднеквадратичного значения шума является его выражение в терминах младших разрядов, хотя оно может быть выражено как среднеквадратичное значение напряжения.
Существуют различные способы описания характеристик аналогового тракта АЦП. На ранней стадии технологии АЦП (более 30 лет назад) не существовало серьезной стандартизации характеристик аналогового тракта, измерительного оборудования и методов или они не были хорошо изучены либо были недоступны. Спустя почти 30 лет производители и заказчики узнали больше об измерении динамических характеристик преобразователей. Спецификации наиболее популярных сегодня преобразователей представлены на рис.2.22. Фактически все спецификации представляют характеристики преобразователя в частотной области. БПФ является основой практически всех измерений и подробно обсуждается в разделе 5 этой книги.
ГИСТОГРАММА, ПОКАЗЫВАЮЩАЯ РАСПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ ВЫХОДНОГО КОДА
ПРИ ДЕЙСТВИИ ШУМА НА ВХОД АЦП
Рис. 2.21
Гармонические искажения Наихудшие гармоники Общие гармонические искажения (THD) Общие гармонические искажения и шум (THD + N) Отношение сигнал-шум и искажения (SINAD, or S/N +D) Эффективное количество разрядов (ENOB) Отношение сигнал-шум (SNR) Аналоговая полоса пропускания (для полного сигнала, для малого сигнала) Динамический диапазон, свободный от гармоник (SFDR) Двухтональные интермодуляционные искажения Многотональные интермодуляционные искажения ОПРЕДЕЛЯЮЩИЕ ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
АЦП
Рис. 2.22
Явления интегральных и дифференциальных нелинейных искажений
Одним из важнейших для понимания аспектов при определении нелинейности АЦП и ЦАП является то, что передаточная функция преобразователя данных имеет особенности, которые отсутствуют в обычных линейных устройствах типа операционных усилителей (ОУ) или усилительных блоков. Полная интегральная нелинейность АЦП обусловлена интегральной нелинейностью входного буфера, УВХ (SHA) и полной интегральной нелинейностью передаточной функции АЦП.
Но дифференциальная нелинейность, которая присутствует исключительно вследствие цифрового кодирования, может значительно изменяться в зависимости от принципов применяемого цифрового кодирования АЦП. Полная интегральная нелинейность дает составляющие искажений, у которых амплитуда изменяется в зависимости от амплитуды входного сигнала. В частности, интермодуляционные составляющие второго порядка увеличиваются на 2 дБ при увеличении сигала на 1 дБ, а составляющие третьего порядка увеличиваются на 3 дБ при повышении уровня сигнала на 1 дБ.
Дифференциальная нелинейность в передаточной функции АЦП порождает гармоники, которые зависят не только от амплитуды сигнала, но и от положения точки дифференциальной нелинейности на передаточной функции АЦП. На рис.2.23 показаны две передаточные функции АЦП, имеющих различную дифференциальную нелинейность. Левая диаграмма показывает погрешность, которая имеет место при наличии нелинейности в середине шкалы. Поэтому сигнал, проходящий через эту точку, и при "больших", и при "малых" сигналах подвергается искажениям, не зависящим от относительной амплитуды сигнала. Правая диаграмма показывает другую передаточную функцию АЦП, которая имеет погрешности дифференциальной нелинейности в точках, соответствующих 1/4 и 3/4 полной шкалы. Сигналы, превышающие 1/2 шкалы АЦП, подвергнутся действию этих искажений, в то время как сигналы, не превышающие 1/2 шкалы размаха, не имеют искажений.
ТИПИЧНЫЙ ВИД ДИФФЕРЕНЦИАЛЬНОЙ
НЕЛИНЕЙНОСТИ (DNL) АЦП/ЦАП
Рис. 2.23
Большинство быстродействующих АЦП разработаны так, чтобы дифференциальная нелинейность равномерно распределялась по всей ширине динамического диапазона АЦП. Поэтому для сигналов, которые находятся в пределах нескольких дБ полной шкалы АЦП, полная интегральная нелинейность передаточной функции определяет гармонические искажения. Для сигналов более низких уровней содержание гармоник определяется дифференциальной нелинейностью и в общем случае не уменьшается с уменьшением амплитуды сигнала.
Нелинейные искажения, наихудшая гармоника, общие нелинейные искажения (THD), общие нелинейные искажения плюс шум (THD + N)
Существует множество способов количественного описания искажений в АЦП. Анализ БПФ может использоваться для измерения амплитуды различных гармоник сигнала. Гармоники входного сигнала могут отличаться от других составляющих искажений их положением в частотном спектре. На рис.2.24 показан 7 МГц входной сигнал, дискретизированный с частотой 20 MSPS, и положение его первых девяти гармоник. Гармоники частоты fa попадают на частоты, равные |±Kfs±nfa|, где n – порядок гармоники и K = 0, 1, 2, 3, .... В общем, только вторая и третья гармоники точно определены в технической документации, потому что они, как правило, наибольшие, хотя в некоторых случаях могут определять значение наихудшей гармоники (worst harmonic). Нелинейные искажения обычно определяются в дБс (децибелы ниже несущей), хотя на звуковых частотах они могут быть определены в процентах. Нелинейные искажения, как правило, определяются при входным сигнале с размахом, близким к полной шкале преобразователя (от 0,5 до 1 дБ ниже полной шкалы для предотвращения амплитудного ограничения), хотя возможно определение их и на любом другом уровне. Для сигналов с размахом, существенно меньшим полной шкалы, из-за дифференциальной нелинейности преобразователя другие составляющие (не прямые гармоники) могут ухудшать характеристики прибора.
РАСПОЛОЖЕНИЕ СОСТАВЛЯЮЩИХ ГАРМОНИЧЕСКИХ
ИСКАЖЕНИЙ: ВХОДНОЙ СИГНАЛ = 7 МГЦ,
СКОРОСТЬ (ЧАСТОТА) ДИСКРЕТИЗАЦИИ = 20 MSPS
Рис. 2.24
Величина полных нелинейных искажений (THD) определяется как отношение среднеквадратичного значения основной частоты сигнала к среднему значению корня из суммы квадратов (root-sum-square) его гармоник (существенны только первые пять). Полные нелинейные искажения АЦП также определяются входным сигналом величиной, близкой к полной шкале АЦП, но могут быть найдены и на любом ином уровне. Полные нелинейные искажения плюс шум (THD + N) являются отношением среднеквадратичного значения основной частоты сигнала к среднему значению корня из суммы квадратов (root-sum-square) его гармоник и всех шумовых компонент (исключая постоянную составляющую).
Ширина полосы, в которой измеряется шум, должна быть задана. В случае БПФ ширина полосы занимает промежуток от 0 до fs/2 (если ширина полосы измерения от 0 до fs/2, THD+N = SINAD – см. ниже).
Показатель сигнал/шум/искажения (SINAD), показатель сигнал/шум (SNR) и эффективное число разрядов (ENOB)
Показатель сигнал/шум/искажения (SINAD) и показатель сигнал/шум (SNR) заслуживают особого внимания, потому что все еще имеются некоторые разногласия между производителями АЦП относительно их точного определения. Сигнал/шум/искажения (SINAD, или S/N+D) – это отношение среднеквадратичного значения амплитуды сигнала к среднему значению корня из суммы квадратов (RSS) всех других спектральных компонентов, включая гармоники, но исключая постоянную составляющую. SINAD является хорошим индикатором общих динамических характеристик АЦП, таких как функция входной частоты, потому что включает все компоненты, которые создают шум (включая тепловой шум) и искажения. Он часто представляется в виде графика для различных амплитуд входного сигнала. Если ширина полосы сигнала и шума одинаковы, то SINAD = THD+N. Типичный график для 12-разрядного АЦП AD9220 с частотой дискретизации 10 MSPS представлен на рис.2.26.
ОТНОШЕНИЕ СИГНАЛ/(ШУМ И ИСКАЖЕНИЯ) (SINAD),
ЭФФЕКТИВНАЯ РАЗРЯДНОСТЬ (ENOB),
ОТНОШЕНИЕ СИГНАЛ/ШУМ (SNR)
Рис. 2.25
SINAD (Отношение сигнала к шуму и искажениям): Отношение среднеквадратичного значения амплитуды сигнала к среднему значению корня из суммы квадратов (RSS) всех остальных составляющих спектра, включая гармоники, но исключая постоянную составляющую. ENOB (Эффективная разрядность): ENOB = SNR (Отношение сигнал/шум или отношение сигнал/шум без гармоник): Отношение среднеквадратичного значения амплитуды сигнала к среднему значению корня из суммы квадратов (RSS) всех остальных составляющих спектра, исключая первые пять гармоник и постоянную составляющую SINAD – 1.76 дБ 6.02 дБ ОТНОШЕНИЕ СИГНАЛ/(ШУМ И ИСКАЖЕНИЯ) (SINAD) И ЭФФЕКТИВНОЕ ЧИСЛО РАЗРЯДОВ (ENOB) ПРИ РАЗЛИЧНЫХ УРОВНЯХ ВХОДНОГО СИГНАЛА 12-РАЗРЯДНОГО, 10 MSPS АЦП AD9220
ЧАСТОТА АНАЛОГОВОГО СИГНАЛА НА ВХОДЕ (МГц)
Рис. 2.26
График SINAD показывает, где характеристики АЦП по переменному току ухудшаются из-за искажений на высоких частотах, причем обычно этот график строится для частот, значительно превышающих частоту Найквиста для оценки характеристик в приложениях, использующих субдискретизацию. SINAD часто преобразуется в эффективное число разрядов (ENOB), используя выражение для теоретического отношения сигнал/шум идеального N-разрядного АЦП: SNR = 6,02N + 1,76dB. Уравнение решается для N, и значение отношения сигнал/шум заменяется на SINAD:
Отношение сигнал/шум (SNR или SNR без гармоник) рассчитывается так же, как и SINAD, за исключением того, что из выражения исключаются гармоники сигнала и оставлены только шумовые составляющие. Практически, необходимо исключить только первые пять доминирующих гармоник. Показатель сигнал/шум будет ухудшаться на высоких частотах, но не так быстро как SINAD, так как из него исключены компоненты гармоник.
Во многих описаниях АЦП довольно свободно принимается, что SINAD равно SNR, так что инженер должен быть внимательным при интерпретации этих характеристик.
Аналоговая ширина полосы
Аналоговая ширина полосы АЦП – это та частота, на которой спектральный выход основной смещенной частоты (как было определено при анализе БПФ) уменьшается на 3 дБ. Она может быть определено как для малого сигнала (полоса пропускания малого сигнала SSBW), так и для сигнала на уровне полной шкалы (полоса пропускания максимального сигнала FPBW). Поэтому между производителями могут встречаться большие различия в характеристиках.
Как и для усилителя, спецификация аналоговой полосы пропускания преобразователя не предполагает, что АЦП поддерживает хорошие характеристики гармонических искажений во всей полосе частот. В действительности, SINAD (или ENOB) большинства АЦП начинает ухудшаться значительно раньше, чем частота входного сигнала приблизится к значению, соответствующему ослаблению на 3 дБ. На рис.2.27 представлены эффективное число разрядов (ENOB) и частотная характеристика входного сигнала, соответствующего полной шкале АЦП с FPBW 1 МГц, но ENOB начинает быстро понижаться на частотах, превышающих 100 кГц.
ЗАВИСИМОСТЬ УСИЛЕНИЯ (ПОЛОСА ПРОПУСКАНИЯ) АЦП И ЭФФЕКТИВНОЙ РАЗРЯДНОСТИ (ENOB) ОТ ЧАСТОТЫ СИГНАЛА ПОКАЗАНЫ ВАЖНЫЕ ПАРАМЕТРЫ СПЕЦИФИКАЦИИ ENOB
Рис. 2.27
Динамический диапазон, свободный от гармоник(SFDR)
Вероятно, наиболее значительным моментом для АЦП, используемых в коммуникационных приложениях, является их динамический диапазон, свободный от гармоник (SFDR). Спецификация SFDR для АЦП аналогична спецификации точки пересечения уравнений третьего порядка для смесителей и малошумящих усилителей (LNA). SFDR АЦП определяется как отношение среднеквадратичного значения амплитуды сигнала к среднеквадратичному значению пикового побочного спектрального состава, измеренного в первой зоне Найквиста от 0 до fs/2. На графике SFDR строится как функция амплитуды сигнала и может быть выражен относительно амплитуды сигнала (дБс) или полной шкалы АЦП (dBFS), как показано на рис.2.28.
СВОБОДНЫЙ ОТ ГАРМОНИК ДИНАМИЧЕСКИЙ
ДИАПАЗОН (SFDR)
Рис. 2.28
Для сигнала, имеющего амплитуду, близкую к полной шкале АЦП, пиковая спектральная линия определяется несколькими первыми гармониками основной частоты. Но когда сигнал опускается на несколько дБ ниже полной шкалы, появляются другие спектральные линии, которые не являются прямыми гармониками входного сигнала. Это, как обсуждалось ранее, происходит из-за дифференциальной нелинейности передаточной функции АЦП. Поэтому, SFDR учитывает все источники искажения, независимо от их происхождения.
Широкополосный 12-разрядный АЦП AD9042 с частотой дискретизации 41 MSPS, является АЦП, разработанным для коммуникационных приложений, где SFDR очень важен. На рис.2.29 представлены характеристики SFDR для входного сигнала 19,5 МГц, дискретизированного с частотой 41 MSPS. Обратите внимание, что минимум SFDR в 80 дБс получен во всей первой зоне Найквиста (от 0 до 20 МГц). На графике также показано значение SFDR, выраженное как dBFS.
В общем случае SFDR существенно больше, чем теоретическое значение отношения сигнал/шум N-разрядного АЦП (6,02N + 1,76 дБ).
Например, 12-разрядный АЦП AD9042 с SFDR 80 дБс имеет типичное отношение сигнал/шум 65 дБс (теоретическое 74 дБ). Это объясняется тем, что есть существенное различие между измерениями искажений и шума. Выигрыш в отношении сигнал/шум БПФ (33 дБ для БПФ с 4096 точками) допускает существование частотных линий значительно ниже наблюдаемого минимального уровня шума. Увеличение разрешающей способности АЦП может увеличивать отношение сигнал/шум АЦП, но не обязательно улучшает его SFDR.
ЗАВИСИМОСТЬ SFDR ОТ ВХОДНОЙ МОЩНОСТИ ДЛЯ 12-РАЗРЯДНОГО 41 MSPS АЦП AD9042
Рис. 2.29
Двухтональные интермодуляционные искажения (IMD)
Двухтональные интермодуляционные искажения (IMD) измеряют, подавая на АЦП два спектрально чистых синусоидальных сигнала с частотами f1 и f2, обычно довольно близкими друг к другу. Амплитуда каждой компоненты устанавливается на 6 дБ ниже полной шкалы для того, чтобы АЦП не входил в ограничение при совпадении сигналов по фазе. На рис.2.30 показано местоположение составляющих второго и третьего порядка. Обратите внимание, что составляющие второго порядка приходятся на те частоты, которые могут быть удалены цифровыми фильтрами. Но составляющие третьего порядка 2f2–f1 и 2f1–f2 располагаются близко к исходным сигналам и их более трудно фильтровать. Если не определено иное, двухтональные интермодуляционные искажения (IMD) относятся к этим составляющим третьего порядка. Значение интермодуляционных искажений выражается в дБс относительно уровня любой из двух первоначальных частот, а не их суммы.
Обратите внимание, что, если частоты имеют значения, близкие к fs/4, то третьи гармоники основных частот могут затруднить идентификацию компонент 2f2–f1 и 2f1–f2. Это происходит потому, что третья гармоника fs/4 равна 3 fs/4 и она, соответственно, порождает компоненту fs – 3 fs/4 = fs/4. Точно также, если две частоты располагаются близко к fs/3, то вторая гармоника может мешать измерениям по той же причине: вторая гармоника fs/3 равна 2 fs/3 и она, соответственно, порождает компоненту fs – 2 fs/3 = fs/3.
СОСТАВЛЯЮЩИЕ 2-ГО И 3-ГО ПОРЯДКА В РЕЗУЛЬТАТЕ ВОЗДЕЙСТВИЯ ДВУХТОНАЛЬНОГО СИГНАЛА f 1 = 5 МГц, f 2 = 6 МГц
Рис. 2.30
Концепция точек пересечения кривых второго и третьего порядка неправильна для АЦП, потому что уровень составляющих искажений изменяется непредсказуемым образом (он не является функцией амплитуды сигнала). АЦП начинает ограничивать сигналы, приближающиеся к полной шкале, не постепенно (точка ограничения на 1 дБ отсутствует). Как только сигнал превышает диапазон изменения входных сигналов АЦП, АЦП действует в качестве жесткого ограничителя, внезапно создавая критические искажения из-за амплитудного ограничения. С другой стороны, для сигналов, значительно меньших полной шкалы, уровень искажений остается относительно постоянным и не зависимым от уровня сигнала.
В коммуникационных приложениях часто измеряется многотональный SFDR. Большим числом тонов более точно моделируется широкополосный частотный спектр систем сотовой телефонии типа AMPS и GSM. На рис.2.31 представлены характеристики 4-тональной интермодуляции 12-разрядного АЦП AD6640 с быстродействием 65 MSPS. Большое значение SFDR увеличивает способность приемника фиксировать слабые сигналы в присутствии сильных и предотвращать маскировку слабых сигналов интермодуляционными помехами сильных.
ТЕСТИРОВАНИЕ МНОГОТОНАЛЬНЫМ СИГНАЛОМ: 12-РАЗРЯДНЫЙ 65 MSPS АЦП AD6640
Рис. 2.31
Уровень собственных шумов (NPR)
П роверка уровня собственных шумов широко применяется для измерения характеристики передачи линии связи, использующей систему с многоканальным доступом с частотным разделением каналов (FDMA) (см. Приложение 4). В типичной FDMA-системе звуковые каналы шириной 4 кГц загружаются в "частотный стек" для передачи через коаксиальный кабель, радиорелейную станцию микроволнового диапазона или спутниковое оборудование. На приемном конце системы FDMA данные демультиплексируются и возвращаются к 4 кГц индивидуальным каналам основной полосы частот. В FDMA системе, имеющей более 100 каналов, сигнал FDMA может быть аппроксимирован Гауссовым шумом с соответствующей шириной полосы.
Индивидуальный 4 кГц канал может быть проверен на предмет собственных шумов, используя узкополосный режекторный фильтр и специально настроенный приемник, который измеряет мощность шума внутри 4 кГц полосы подавления (см. рис.2.32).
Измерения уровня собственных шумов (NPR) производятся весьма просто. Среднеквадратичное значение мощности шума сигнала внутри полосы подавления измеряется узкополосным приемником при отключенном режекторном фильтре. Затем подключается режекторный фильтр и измеряется остаточный шум внутри канала. Отношение этих двух значений, выраженное в дБ, является уровнем собственных шумов (NPR). Для соответствующей характеристики системы проверяется несколько интервалов частот в пределах шумовой полосы (в области низких, средних и высоких частот). Измерение уровня собственных шумов в АЦП осуществляется подобным же образом, за исключением использования аналогового приемника, который заменен буферной памятью и процессором БПФ.
ИЗМЕРЕНИЕ УРОВНЯ СОБСТВЕННЫХ ШУМОВ (NPR)
Рис. 2.32
Обычно уровень собственных шумов (NPR) представляется на графике. График NPR отображает функцию среднеквадратичного значения уровня шума в пиковом диапазоне системы. Для очень низкого уровня широкополосного сигнала нежелательным (в нецифровых системах) является, прежде всего, тепловой шум, который независим от уровня входного широкополосного сигнала. В этой части кривой увеличение на 1 дБ подаваемого широкополосного входного сигнала вызывает увеличение уровня собственных шумов на 1 дБ. По мере увеличения уровня широкополосного входного сигнала, усилители в системе начинают работать с перегрузкой, создавая интермодуляционные помехи, которые увеличивают уровень шума системы. По мере того, как входной сигнал продолжает увеличиваться, усиливаются эффекты "шумовой перегрузки" и NPR существенно уменьшается. FDMA-системы обычно работают в режиме, когда уровень подаваемого широкополосного сигнала на несколько дБ ниже точки максимума уровня собственных шумов.
В цифровой системе с АЦП шум в пределах интервала является, прежде всего, шумом квантования, если используются низкие уровни входного широкополосного сигнала.
В этой части кривая NPR имеет линейную зависимость. По мере того, как уровень широкополосного входного сигнала увеличивается, некоторое время сохраняется линейное соответствие между уровнем входного шума и NPR. Но на некотором уровне шум амплитудного ограничения, вызванный жестким ограничивающим действием АЦП, начинает преобладать. Теоретическая кривая для 10-, 11- и 12-разрядных АЦП представлена на рис.2.33 (см. Приложение 5).
В многоканальных высокочастотных коммуникационных системах NPR может, также, использоваться для моделирования искажений, вызванных большим количеством индивидуальных каналов, подобно тому, как это имеет место в FDMA-системе. При этом режекторный фильтр помещается между источником шума и АЦП, и результат расчета БПФ используется вместо аналогового приемника. Для AD9042 ширина полосы режекторного фильтра устанавливается в несколько мегагерц, как показано на рис.2.34. Здесь уровень собственных шумов (NPR) – это глубина режекции. Идеальный АЦП генерирует только шум квантования внутри полосы режекции, но на практике существуют дополнительные шумовые компоненты из-за интермодуляционных искажений, вызванных нелинейностью АЦП. Обратите внимание, что уровень собственных шумов достигает 60 дБ, тогда как расчетное значение равно 62,7 дБ.
ТЕОРЕТИЧЕСКИЙ УРОВЕНЬ ШУМА (NPR) ДЛЯ 10, 11 И 12-РАЗРЯДНЫХ АЦП
Рис. 2.33
12-РАЗРЯДНЫЙ 41 MSPS АЦП AD9042:
ИЗМЕРЕННЫЙ NPR 60 ДБ
(РАСЧЕТНОЕ ЗНАЧЕНИЕ 62,7ДБ)
Рис. 2.34
Дрожание апертуры и апертурная задержка
Другая причина того, что отношение сигнал/шум (SNR) АЦП уменьшается с увеличением входной частоты, может быть выведена из рис.2.35, который показывает эффекты дрожания фазы в дискретизаторе АЦП (или внутреннем в УВХ). Дрожание фазы вызывает ошибку напряжения, которая является функцией скорости нарастания сигнала и приводит к существенному ухудшению отношения сигнал/шум, как показано на рис.2.36. Это довольно серьезный эффект, особенно на высоких частотах входного сигнала. Поэтому, должна соблюдаться особая осторожность при минимизации фазового шума в дискретизаторах любой системы.
Эта осторожность должна распространяться на все компоненты, в которых присутствуют тактовые сигналы: непосредственно генератор (например, таймер серии 555 не отвечает требованиям, но даже кварцевый генератор может создавать проблемы, если он используется в активном устройстве совместно с шумной логикой); тракт передачи (эти тактовые сигналы очень уязвимы к помехам всех видов) и фазовый шум, вводимый в АЦП или ЦАП. Общим источником фазового шума в преобразователе является дрожание апертуры в общей цепи УВХ (SHA).
ВЛИЯНИЕ ДРОЖАНИЯ АПЕРТУРЫ
И ФАЗОВОГО ШУМА ТАКТОВОГО ГЕНЕРАТОРА
Рис. 2.35
Два десятилетия назад схемы дискретизации АЦП создавались отдельно из УВХ (SHA) и АЦП. Проектирование интерфейса было трудным делом, и главная причина этого заключалась в дрожании апертуры в УВХ. Сегодня большинство систем дискретизации использует схемы дискретизации АЦП с интегрированной схемой УВХ. Дрожание апертуры УВХ может быть не определено явным образом в спецификации, но это не служит поводом для беспокойства, если SNR или ENOB ясно определены. Иными словами, гарантия определенного отношения сигнал/шум (SNR) является неявной гарантией определенного адекватного значения дрожания апертуры. А использование дополнительной высококачественной схемы УВХ иногда приводит к улучшению значений эффективного числа разрядов (ENOB) на высоких частотах даже в лучших дискретизирующих АЦП и может оказаться более выгодным, чем замена АЦП на более дорогую модель.
Необходимо отметить, что существует также фиксированный компонент, который присутствует при определении апертуры дискретизации АЦП. Этот компонент, обычно называемый временем эффективной апертурной задержки, не дает ошибки. Его наличие приводит к появлению интервала между временем команды АЦП на дискретизацию и временем, когда получен реальный отсчет (см. рис.2.37). Интервал может быть положительным или отрицательным. Изменение или допуск этого параметра важны в приложениях с одновременной дискретизации с помощью двух АЦП или в других приложениях типа I- и Q-демодуляции, где два АЦП требуют совместной синхронизации.
УХУДШЕНИЕ SNR ИЗ-ЗА ДРОЖАНИЯ ФАЗЫ СИГНАЛА СИНХРОНИЗАЦИИ АЦП
Рис. 2.36
ВРЕМЯ ЭФФЕКТИВНОЙ АПЕРТУРНОЙ ЗАДЕРЖКИ
Рис. 2.37
Д ИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦАП
Очевидно, что для цифро- аналогового преобразователя наиболее важными являются такие характеристики сигнала, как время установки (settling time), всплеск сигнала вследствие перерегулирования при изменении сигнала на выходе ЦАП, называемый далее ложным сигналом (выбросом, glitch), искажения и свободный от помех динамический диапазон сигнала (SFDR).
Время установки ЦАП – это время от начала изменения цифрового кода до момента, когда сигнал стабилизируется в пределах некоторого диапазона ошибки, как это показано на рис.2.38. Сравнивать времена установки усилителей трудно, так как их диапазоны ошибки могут отличиться от усилителя к усилителю, но диапазон ошибки ЦАП практически не меняется и равен ±1 или ±½ LSB.
Время установки ЦАП состоит из четырех различных периодов: время переключения (в течение которого цифровое переключение осуществлено, но на выходе нет изменений), переходное время (slewing time) (в течение которого скорость изменения выходного сигнала ограничена скоростью нарастания на выходе ЦАП), время восстановления (recovery time) (когда ЦАП восстанавливает значение после быстрого перехода и может быть выброс на фронте) и линейное время установки (linear settling time) (когда значение на выходе ЦАП приближается к его конечной величине экспоненциально или почти экспоненциально). Если переходное время мало по сравнению с тремя другими (как это обычно бывает в случае с токовыми выходами ЦАП), то время установки не будет существенно зависеть от перепада уровня выходного сигнала. С другой стороны, если переходное время занимает существенную часть общего времени, то время установки будет тем больше, чем больше величина перепада.
ВРЕМЯ УСТАНОВЛЕНИЯ ЦАП
Рис. 2.38
В идеале изменения на выходе ЦАП от одной величины до другой должны проходить монотонно. На практике возможно появление выброса фронта (overshoot), отрицательного выброса перед фронтом (undershoot) или то и другое одновременно (см.
рис.2.39). Это неконтролируемое состояние выхода ЦАП в течение перехода известно как ложный сигнал. Он может являться результатом двух явлений: емкостной связи цифровых переходов с аналоговым выходом и свойствами некоторых ключей в ЦАП, работающих более быстро, чем другие, и создающих временные выбросы по уровню.
ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА ЦАП (С ПАРАЗИТНЫМИ ВЫБРОСАМИ)
Рис. 2.38
Емкостная связь часто дает примерно равные положительные и отрицательные выбросы (иногда называемые дуплетом ложного сигнала), которые далее в большей или меньшей степени удается компенсировать. Ложный сигнал, появляющийся вследствие несинхронности переключения, в общем случае униполярен, имеет большую амплитуду и представляет собой гораздо большую проблему.
Для оценки ложных сигналов измеряют площадь, огибаемую фронтом такого сигнала, и иногда неточно называемую энергией ложного сигнала. Употребление термина "энергия ложного сигнала" неправильно, так как площадь под кривой ложного сигнала измеряется вольт-секундами (Volt-seconds) (или более вероятно µV- секунды или pV- секунды). Пиковая площадь под кривой ложного сигнала – это площадь под максимальным положительным или отрицательным импульсом ложного сигнала. Площадь импульса ложного сигнала – это область под вольт-секундной кривой, которая может быть рассчитана после аппроксимации формы сигнала треугольниками и вычисления их площади посредством вычитания отрицательной площади из положительной. Величина ложного сигнала, порождаемого переходом между кодами 0111...111 и 1000...000, обычно является самой большой. Ложные сигналы в других точках перехода кода (таких как 1/4 и 3/4 полной шкалы) обычно имеют меньшую величину. На рис.2.40 отмечен ложный сигнал быстрого ЦАП с малым значением такого сигнала в середине его динамического диапазона. Пиковые и импульсные площади ложного сигнала рассчитываются с использованием треугольников, как это было описано выше. Время установки измеряется с момента, когда сигнал покидает начальный диапазон ошибки в 1 LSB, и до момента, когда он входит и остается в пределах конечного диапазона ошибки в 1 LSB.
Размер шага между областями перехода также равен 1 LSB.
ВЫБРОСЫ СИГНАЛА ЦАП:
СУММАРНАЯ ПЛОЩАДЬ ИМПУЛЬСА – 1.34 пВ·с
ВРЕМЯ УСТАНОВЛЕНИЯ – 4.5 нс
Рис. 2.40
Время установки ЦАП важно в таких приложениях, как блок развертки RGB-сигнала в мониторах, а характеристики в частотной области типа SFDR в общем случае более важны в телекоммуникациях.
Если мы рассмотрим спектр сигнала, преобразованного в ЦАП из цифровой формы, то обнаружим, что, в дополнение к ожидаемому спектру (который будет содержать одну или больше частот, в зависимости от природы восстановленного сигнала), в нем также будет присутствовать шум и составляющие искажений. Искажения могут быть определены в терминах нелинейных искажений, динамического диапазона, свободного от помех (SFDR), интермодуляционных искажений или всех вышеперечисленных вместе. Под нелинейными искажениями понимается отношение высших гармоник к гармонике основной частоты, на которой восстановлен чистый (теоретически) синусоидальный сигнал. Эти искажения являются наиболее общей характеристикой искажений. Динамический диапазон, свободный от помех (SFDR) – это отношение энергии наибольшей из гармоник (обычно – это гармоника основной частоты, но не обязательно) к энергии основной частоты.
При восстановлении с помощью ЦАП синусоидального сигнала, сгенерированного в системе прямого цифрового синтеза (DDS), зависимые от кода ложные сигналы формируют гармоники как внутри полосы, так и за ее пределами. Сигнал проходит через уровень, соответствующий середине шкалы, дважды за один цикл. Поэтому ложный сигнал имеет вторую синусоидальную гармонику, как показано на рис.2.41. Обратите внимание, что гармоники более высокого порядка, составляющие которых попадают в основную полосу Найквиста (от 0до fs /2), не фильтруются.
ПРОЯВЛЕНИЕ КОД-ЗАВИСИМЫХ ВЫБРОСОВ СИГНАЛА В СПЕКТРЕ ВЫХОДНОГО СИГНАЛА
Рис. 2.41
Руководствуясь одной лишь характеристикой площади под кривой ложного сигнала, трудно предсказать нелинейное искажение или SFDR. Другие факторы, такие как полная линейность ЦАП, также способствуют возникновению искажений.
Поэтому, общепринята проверка восстановительной способности ЦАП в частотной области (с использованием анализатора спектра) на различных тактовых и сигнальных частотах, как показано на рис.2.43. Типичное значение SFDR для 14-разрядного ЦАП AD9772 представлено на рис.2.44. Тактовая частота равна 65 MSPS и сигнальная частота анализируется до 25 MГц. Как и в случае с АЦП, шум квантования будет проявляться в виде увеличенного нелинейного искажения, если отношение между частотой синхронизации и выходной частотой ЦАП представляется целым числом. Таких отношений нужно избегать при измерении SFDR.
Разрешающая способность ЦАП Общая нелинейность Дифференциальная нелинейность Код-зависимые выбросы Отношение тактовой частоты к выходной (даже для идеального ЦАП) Аналитический подход затруднен! ИСТОЧНИКИ ИСКАЖЕНИЙ В ЦАП СИНТЕЗАТОРОВ ЧАСТОТЫ (DDS)
Рис. 2.42
СХЕМА ИЗМЕРЕНИЯ SFDR ЦИФРО-АНАЛОГОВОГО ПРЕОБРАЗОВАТЕЛЯ
Рис. 2.43
Спад частотной характеристики (Rolloff ) ЦАП sin (x)/x
Выходной сигнал ЦАП может быть представлен в виде ряда прямоугольных импульсов шириной, равной обратной величине тактовой частоты, как показано на рис.2.45. Обратите внимание, что восстановленная амплитуда сигнала составляет -3,92 дБ на частоте Найквиста fс /2. Для компенсации этого эффекта в большинстве случаев достаточно использовать инверсный фильтр sin(x)/x. Значения составляющих основной частоты также ослабляются функцией sin(x)/x.
СПЕКТР ВЫХОДОНОГО СИГНАЛА ЦАП С ОГИБАЮЩЕЙ ВИДА SIN X/X (АМПЛИТУДА НОРМАЛИЗОВАННАЯ)
Рис. 2.45
С ПИСОК ЛИТЕРАТУРЫ
Осокин Ю.В., Судьин С.Л., Федорков Б.Г "Параметры, области применения и перспективы развития полупроводниковых преобразователей информации// микроэлектроника и полупроводниковые приборы" под редакцией А.А. Васенкова и Я.А. Федотова. М.: Радио и связь. 1983. Федорков Б.Г, Телец В.А. "Микросхемы ЦАП и АЦП: функционирование, параметры, применение" - М. Энергоатомиздат 1990. W. R. Bennett, “Spectra of Quantized Signals”, Bell System Technical Journal, No. 27, July 1948, pp. 446-472. Steve Ruscak and Larry Singer, Using Histogram Techniques to Measure A/D Converter Noise, Analog Dialogue , Vol. 29-2, 1995. M.J.
Tant, The White Noise Book, Marconi Instruments, July 1974. G.A. Gray and G.W. Zeoli, Quantization and Saturation Noise due to A/D Conversion, IEEE Trans. Aerospace and Electronic Systems, Jan. 1971, pp. 222-223. Chuck Lane, A 10-bit 60MSPS Flash ADC, Proceedings of the 1989 Bipolar Circuits and Technology Meeting, IEEE Catalog No. 89CH2771-4, September 1989, pp. 44-47. F.D. Waldhauer, Analog to Digital Converter, U.S. Patent 3-187-325, 1965. J.O. Edson and H.H. Henning, Broadband Codecs for an Experimental 224Mb/s PCM Terminal, Bell System Technical Journal, 44, November 1965, pp. 1887-1940. J.S. Mayo, Experimental 224Mb/s PCM Terminals, Bell System Technical Journal, 44, November 1965, pp. 1813-1941. Hermann Schmid, Electronic Analog/Digital Conversions, Van Nostrand Reinhold Company, New York, 1970. Carl Moreland, An 8-bit 150MSPS Serial ADC, 1995 ISSCC Digest of Technical Papers, Vol. 38, p. 272. Roy Gosser and Frank Murden, A 12-bit 50MSPS Two-Stage A/D Converter, 1995 ISSCC Digest of Technical Papers , p. 278. Carl Moreland, An Analog-to-Digital Converter Using Serial-Ripple Architecture, Masters' Thesis, Florida State University College of Engineering, Department of Electrical Engineering, 1995. Walt Kester, Drive Circuitry is Critical to High-Speed Sampling ADCs, Electronic Design Special Analog Issue, Nov. 7, 1994, pp. 43-50. Walt Kester, Basic Characteristics Distinguish Sampling A/D Converters, EDN, Sept. 3, 1992, pp. 135-144. Walt Kester, Peripheral Circuits Can Make or Break Sampling ADC Systems, EDN , Oct. 1, 1992, pp. 97-105. Walt Kester, Layout, Grounding, and Filtering Complete Sampling ADC System, EDN , Oct. 15, 1992, pp. 127-134. Joey Doernberg, Hae-Seung Lee, David A. Hodges, Full Speed Testing of A/D Converters, IEEE Journal of Solid State Circuits, Vol. SC-19, No. 6, Dec. 1984, pp. 820-827. Brendan Coleman, Pat Meehan, John Reidy and Pat Weeks, Coherent Sampling Helps When Specifying DSP A/D Converters, EDN, October 15, 1987, pp. 145-152. James J.Colotti, Digital Dynamic Analysis of A/D Conversion Systems Through Evaluation Software Based on FFT/DFT Analysis, RF Expo East 1987 Proceedings, Cardiff Publishing Co., pp. 245-272. Dan Sheingold, Editor, Analog-to-Digital Conversion Handbook, Third Edition, Prentice-Hall, 1986. Lawrence Rabiner and Bernard Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, 1975. Matthew Mahoney, DSP-Based Testing of Analog and Mixed-Signal Circuits, IEEE Computer Society Press, Washington, D.C., 1987. IEEE Trial-Use Standard for Digitizing Waveform Recorders, No. 1057-1988. Richard J. Higgins, Digital Signal Processing in VSLI, Prentice-Hall, 1990. Howard E. Hilton, A 10MHz Analog-to-Digital Converter with 110dB Linearity, H.P. Journal , October 1993, pp. 105-112.
Квантование аналогового сигнала по времени
Концепции квантования по времени и амплитуде аналогового сигнала показаны на рисунке 1. Дискретизация непрерывных аналоговых данных должна осуществляться с интервалом времени ts=1/fs, который должен быть тщательно выбран для гарантированно точного представления первоначального аналогового сигнала. Ясно, что чем больше будет взято отсчетов на интервале времени (больше частота дискретизации), тем более точным будет представление сигнала в цифровом виде, а при уменьшении количества отсчетов (уменьшении частоты дискретизации) может быть достигнута точка, где сигнал может быть потерян. Это следует из известного критерия Найквиста, показанного на рисунке 2.
КРИТЕРИЙ НАЙКВИСТА
Частота дискретизации fs сигнала с шириной полосы fa должна удовлетворять условию fs > 2fa, в противном случае информация о сигнале будет потеряна Эффект наложения спектров возникает, когда fs < 2fa Эффект наложения спектров широко используются в таких задачах, как прямое преобразование ПЧ в цифровую формуРисунок 2 Критерии Найквиста.
Проще говоря, критерий Найквиста требует, чтобы частота дискретизации была по крайней мере вдвое больше полосы сигнала, в противном случае информация о сигнале будет потеряна. Если частота дискретизации меньше удвоенной полосы аналогового сигнала, возникает эффект, известный как наложение спектров (aliasing).
Для понимания смысла наложения спектров как во временной, так и в частотной областях сначала рассмотрим случай представления во временной области выборки одного тонального сигнала синусоидальной формы, показанный на рисунке 3. В этом примере частота дискретизации fs лишь немного больше частоты аналогового входного сигнала fa, что не удовлетворяет критерию Найквиста. Обратите внимание, что в результате сделанная выборка соответствует сигналу, частота которого равна разности частот дискретизации и частоты исходного сигнала fs-fa. Та же самая ситуация в частотной области приведена на рисунке 4 b.
Теперь рассмотрим дискретизацию одиночного синусоидального сигнала с частотой fa
идеальным дискретизатором (см.
рис.2.4, A) с частотой следования дельта импульсов fs. Пусть, fs>2fa. В частотном спектре на выходе дискретизатора видны гармоники частоты дискретизации fs, промодулированные исходным сигналом, то есть появляются образы сигнала на частотах, равных |±Kfs
±fa|, где K = 1, 2, 3, 4, ...

Рисунок 3 Эффект наложения спектров во временной области.

Рисунок 4 Спектр дискретизированного аналогового сигнала
А-низкочастотного B-полосового. Полоса сигнала по Котельникову определяется как спектр от постоянного тока до fs/2. Частотный спектр разделен на бесконечное число зон Найквиста, каждая по 0,5 fs. На практике идеальный дискретизатор перемещает все образы в полосу от 0 до fs/2 и накладывает их на сигнал в первой зоне Котельникова.
Теперь рассмотрим случай, когда частота сигнала выходит за пределы первой зоны Котельникова (рис. 2.4 B). При частоте сигнала немного меньшей частоты дискретизации, временная диаграмма приведена на рисунке 3. Обратите внимание, что несмотря на то, что сигнал находится вне первой зоны Найквиста, его составляющая fs-fa попадает внутрь этой зоны. Возвращаясь к рис.2.4 A, становится ясно, что, если мешающий сигнал появляется на любом из образов частоты fa, он тут же переносится на частоту fa, приводя, таким образом, к появлению мешающего частотного компонента в первой зоне Котельникова.
Такой процесс подобен работе аналогового смесителя. Это означает, что перед дискретизатором требуется фильтрация, подавляющая компоненты, частоты которых находятся вне полосы Котельникова и после дискретизации попадают в ее пределы. Рабочая характеристика фильтра будет зависеть от того, как близко частота внеполосного сигнала отстоит от fs/2, а также величиной требуемого подавления.
Микропроцессоры и цифровая обработка сигналов
В процессе изучения курса микропроцессоры и цифровая обработка сигналов приобретаются знания по разработке и анализу схем, построенных на сигнальных процессорах. Эта дисциплина ориентирована на применение методов цифровой обработки сигналов в аппаратуре связи.
В процессе изучения предмета рассматривается устройство и принцип действия аналого-цифровых, цифро-аналоговых, а также сигнальных процессоров.
Сигнальные процессоры изучаются на примере микросхем семейства TMS320LC54x. В процессе изучения сигнальных процессоров приобретаются навыки составления принципиальных схем и написания программ. Изучаются языки программирования низкого (ассемблер) и высокого уровня (СИ), предназначенные для написания программ для сигнальных процессоров.
Основные определения курса: АЦП, ЦАП, микропроцессор, сигнальный процессор, программные и аппаратные средства систем цифровой обработки данных, многопроцессорные системы, структурно- модульное программирование, отладка программного обеспечения.
Курс микропроцессоры и цифровая обработка сигналов для заочной формы обучения в большей степени ориентирован на самостоятельную работу студентов и разбит на три этапа:
(10ч) (2ч) и лабораторные работы (8ч)Перечень литературы по дисциплине Микропроцессоры и цифровая обработка сигналов
|
Авторы |
Наименование | Год издания | |
| Ж. Макс | Методы и техника обработки сигналов при физических измерениях | 1983 | |
| Ричард Блейхут | 1986 | ||
| Федорков Б.Г, Телец В.А. | Микросхемы ЦАП и АЦП: функционирование, параметры, применение | 1990 | |
| Walt Kester | 2000 | ||
| Материалы сервера | (англ.) | ||
| Материалы сервера | (англ.) | ||
| Материалы сервера | (рус.) | ||
| Материалы сервера | (рус.) |
Погрешности дискретизатора
До сих пор предполагалось, что квантование по времени производится дельта импульсами. Однако это математическая абстракция. Обычно ключ дискретизатора открывается на определённое время, достаточное для запоминания аналогового сигнала на конденсаторе (даже если этот конденсатор паразитный). Теперь образы сигнала уже нельзя считать распространяющимися до бесконечности. Такая цепь обычно называется интегрирующей и её импульсная характеристика приведена на рисунке 5.
 Рисунок 5 Нарастание напряжения на входе дискретизатора при открывании ключа. |  Рисунок 6 Амплитудно-частотная характеристика дискретизатора |
Именно эта характеристика определяет время открывания ключа дискретизатора, достаточное для установления напряжения, меньшего половины младшего разряда АЦП. Такой режим работы дискретизатора называется режимом слежения. Частотная характеристика этой цепи приведена на рисунке 6.
Теперь образы сигналов не будут распространяться до бесконечности. Амплитуда образа будет зависеть от частотной характеристики цепи заряда конденсатора. На рисунках 5 и 6 приведена частотная характеристика простейшей цепи заряда. Однако на высоких частотах необходимо учитывать переходный процесс более сложных цепей таких как индуктивность проводников корпуса, влияние входных и выходных ёмкостей усилителей. В результате переходная характеристика становится более сложной. В соответствии с ней изменится и ёё частотная характеристика. Пример импульсной и частотной характеристик такой цепи приведён на рисунках 7 и 8.
 Рисунок 7 |  Рисунок 8 |
Кроме частотных характеристик на точность преобразования аналогового сигнала в цифровую форму существенное значение имеет точность временного положения импульса дискретизации. В реальных схемах для дискретизации аналогового сигнала используются генераторы сигналов с конечной длительностью фронтов. Временное положение фронтов сигнала зависит от стабильности генераторов сигнала, порога срабатывания логических схем и уровня помех на шинах питания и заземления микросхем.
В дискретизаторах, работающих в режиме слежения, временное положение, при котором считывается аналоговый сигнал определяется задним фронтом стробирующего импульса. Время открывания ключа зависит от постоянной времени паразитных элементов схемы. Всё это приводит к ограничению полосы частот сигнала, преобразуемого в цифровую форму.
В качестве альтернативного режима работы дискретизатора предлагается интегрирующий режим работы. В этом режиме работы используется начальный участок переходной характеристики схемы. На этом участке напряжение на выходе линейно растёт при подаче на вход постоянного напряжения, то есть осуществляется интегрирование входного сигнала. При этом напряжение на конденсаторе после окончания стробирующего импульса будет пропорционально энергии входного сигнала, длительности и формы стробирующего импульса. Длительность и форма стробирующего сигнала может быть при этом учтена как константа. Уменьшение напряжения по сравнению с режимом слежения может быть скомпенсировано дополнительным усилителем на входе АЦП. Основное преимущество такого режима работы заключается в усреднении влияния переднего и заднего фронта, то есть большая верность преобразования сигнала. Кроме того уменьшается время стробирования, т.к. используется только начальный участок переходной характеристики схемы.
ПОГРЕШНОСТИ ПО ПЕРЕМЕННОМУ ТОКУ В ПРЕОБРАЗОВАТЕЛЯХ ДАННЫХ
В течение последнего десятилетия основное применение АЦП и ЦАП находят в дискретизации и восстановлении аналоговых сигналов переменного тока. Очень упрощенно, дискретная система – это система, где мгновенное значение сигнала переменного тока оцифровывается с одинаковыми интервалами. Полученные цифровые коды могут использоваться для сохранения формы сигнала (на компакт-дисках CD или цифровых магнитных лентах DAT), для сложных вычислений с отсчетами (цифровая обработка сигнала DSP), для фильтрации, компрессии и других операций. Обратная операция – восстановление – требуется, когда ряд цифровых кодов подается на ЦАП для восстановления формы аналогового сигнала. Здесь ярким примером является CD- или DAT-плеер, но эта технология очень широко используется также в телекоммуникации, радио, синтезаторах и во многих других областях.
Преобразователи данных, используемые в таких устройствах, должны иметь высокую производительность при работе с сигналами переменного тока, но могут не требовать хороших характеристик по постоянному току.
Первые высококачественные преобразователи, разработанные для таких устройств, обычно создавались с хорошими характеристиками по переменному току, но плохими или ненормированными характеристиками по постоянному току. Сегодня существуют более приемлемые проектные компромиссы, и большинство преобразователей имеют гарантированные характеристики по постоянному и переменному току. Тем не менее, ЦАП для цифровой звукозаписи, которые должны быть чрезвычайно конкурентоспособны по цене, продаются со сравнительно низкими характеристиками по постоянному току, но не из-за низкой производительности по постоянному току, а из-за отсутствия проверки качества в ходе производства.
Если обсуждение параметров по постоянному току можно производить одновременно и для ЦАП, и для АЦП, то их характеристики по переменному току слишком различаются и потому заслуживают раздельного рассмотрения.
Содержание лекций микропроцессоры и цифровая обработка сигналов
Виды АЦП Виды ЦАП Подключение АЦП и ЦАП к сигнальному процессору.
СТАТИЧЕСКАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АЦП И ЦАП И ПОГРЕШНОСТИ ПО ПОСТОЯННОМУ ТОКУ
Наиболее важным моментом, характеризующим и ЦАП, и АЦП является тот факт, что их входы или выходы являются цифровыми, а это означает, что сигнал дискретизирован по уровню. То есть N-разрядное слово представляется одним из 2N возможных состояний, поэтому у N-разрядного ЦАП (с фиксированным источником опорного напряжения) может быть только 2N значений аналогового сигнала, а АЦП может выдавать только 2N различных значений двоичного кода. Аналоговые сигналы могут быть при этом представлены в виде напряжений или токов.
Разрешающая способность АЦП или ЦАП может быть выражена несколькими различными способами: весом младшего разряда (LSB), долей от полной шкалы размером в один миллион (ppm FS), милливольтами (мВ) и т.д. Различные устройства (даже от одного производителя) определяются по-разному, так что для успешного сравнения устройств пользователи АЦП и ЦАП должны уметь преобразовывать различные характеристики. Некоторые значения младшего значащего разряда (LSB) приведены в таблице 1.
Таблица 1. Квантование: значение младшего значащего бита(LSB)
| Разреш. способность N | 2N | Напряжение полной шкалы 10В | ppm FS | % FS | dB FS |
| 2-бит | 4 | 2.5 В | 250000 | 25 | -12 |
| 4-бит | 16 | 625 мВ | 62500 | 6.25 | -24 |
| 6-бит | 64 | 156 мВ | 15625 | 1.56 | -36 |
| 8-бит | 256 | 39.1 мВ | 3906 | 0.39 | -48 |
| 10-бит | 1024 | 9.77 мВ (10 мВ) | 977 | 0.098 | -60 |
| 12-бит | 4096 | 2.44 мВ | 244 | 0.024 | -72 |
| 14-бит | 16384 | 610 мкВ | 61 | 0.0061 | -84 |
| 16-бит | 65536 | 153 мкВ | 15 | 0.0015 | -96 |
| 18-бит | 262144 | 38 мкВ | 4 | 0.0004 | -108 |
| 20-бит | 1048576 | 9.54 мкВ (10 мкВ) | 1 | 0.0001 | -120 |
| 22-бит | 4194304 | 2.38 мкВ | 0.24 | 0.000024 | -132 |
| 24-бит | 16777216 | 596 нВ* | 0.06 | 0.000006 | -144 |
*600 нВ - это тепловой шум в полосе частот 10кГц, возникающий на резисторе R=2.2 кОм при 25°C
Легко запомнить: 10-разрядное квантование при значении полной шкалы FS = 10В соответствует LSB = 10 мВ, точность 1000 ppm или 0.1%. Все остальные значения можно вычислить умножением на коэффициенты, равные степени числа 2.
Прежде чем рассматривать различные архитектуры АЦП и ЦАП, необходимо обсудить ожидаемые характеристики и важнейшие параметры цифро-аналоговых и аналого-цифровых преобразователей.
Ниже будет рассмотрено определение погрешностей и технических требований, предъявляемых к АЦП и ЦАП. Это важно для понимания сильных и слабых сторон различных архитектур АЦП и ЦАП.
Первые преобразователи данных применялись в области измерения и управления, где точное значение времени преобразования обычно не имело значения, и скорость передачи данных была невелика. В таких устройствах важны характеристики АЦП и ЦАП по постоянному току, а характеристики, связанные с синхронизацией и характеристики по переменному току не имеют существенного значения. Сегодня ко многим, если не к большинству преобразователей, используемых в системах дискретизации и восстановления сигнала, предъявляются жесткие требования к характеристикам по переменному току (характеристики по постоянному току могут быть не существенны).
На рисунке 1 представлена идеальная функция передачи однополярного 3-разрядного ЦАП, а на рисунке 2 - однополярного 3-разрядного АЦП. В ЦАП входной и выходной сигналы квантованы, и график содержит восемь точек. Независимо от способа аппроксимации этой функции, важно помнить, что реальной характеристикой передачи является не линия, а множество дискретных точек.

Рисунок 1. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ИДЕАЛЬНОГО 3-РАЗРЯДНОГО ЦАП

Рисунок 2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ИДЕАЛЬНОГО 3-РАЗРЯДНОГО АЦП
Входной аналоговый сигнал АЦП не квантован, но его выходной сигнал является результатом квантования. Сквозная характеристика АЦП состоит из восьми горизонтальных прямых (при изучении смещения, усиления и линейности АЦП мы будем рассматривать линию, соединяющую средние точки этих отрезков). В любом случае полная цифровая шкала (все "1") соответствует полной аналоговой шкале (опорное напряжение или опорное напряжение умноженное на какой либо коэффициент).
Переходы идеального АЦП к следующему цифровому коду происходят, начиная с напряжения, равного половине младшего разряда до напряжения, меньшего напряжения полной шкалы на половину младшего разряда. Так как аналоговый сигнал на входе АЦП может принимать любое значение, а выходной цифровой сигнал квантуется, может существовать различие до половины младшего разряда между реальным входным аналоговым сигналом и соответствующим ему значением выходного цифрового сигнала.
Этот эффект известен как ошибка (погрешность) или неопределенность квантования и показан на рисунке 2. В устройствах, использующих сигналы переменного тока, эта ошибка квантования приводит к шуму квантования.
В АЦП и ЦАП используются много видов цифровых кодов: двоичные коды, двоичные коды со смещением, коды с дополнением до 1, с дополнением до 2, код Грея, двоично-десятичный код и другие. Здесь нас будут интересовать главным образом проблемы, связанные с аналоговым трактом АЦП и ЦАП. Для иллюстрации этих проблем будет использоваться простой двоичный код или двоичный код со смещением без рассмотрения преимуществ и недостатков этих и любых других способов цифрового кодирования.
В примерах на рисунках 1 и 2 применяются униполярные преобразователи, работающие с сигналом только одной полярности. Это самый простой тип, но в реальных устройствах более полезны биполярные преобразователи. Имеется два типа биполярных преобразователей. Более простой из них - это просто униполярный преобразователь с отрицательным смещением на величину, соответствующую единице старшего разряда (MSB), (во многих преобразователях можно переключать это смещение, чтобы использовать их и как униполярные, и как биполярные). Другой, более сложный тип, известен как знаковый АЦП (sign- magnitude) и имеет кроме N информационных разрядов дополнительный разряд, который показывает знак аналогового сигнала. Знаковые ЦАП применяется довольно редко, на знаковых АЦП сконструированы большинство цифровых вольтметров (DVM).
В АЦП и ЦАП различают четыре типа погрешностей по постоянному току: погрешность смещения, погрешность усиления и два типа погрешностей, связанных с линейностью. Погрешности смещения и усиления АЦП и ЦАП аналогичны погрешностям смещения и усиления в усилителях. На рисунке 3 показано преобразование биполярных входных сигналов (хотя погрешность смещения и погрешность нуля, идентичные в усилителях и униполярных АЦП и ЦАП, различны в биполярных преобразователях, и это следует учитывать). Характеристики передачи и ЦАП, и АЦП могут быть выражены как D=K+GA, где D - цифровой код, А - аналоговый сигнал, K и G - константы.
В униполярном преобразователе K равно 0, в биполярном преобразователе со смещением - 1 старшего значащего разряда. Погрешность смещения - это величина, на которую фактическое значение K отличается от идеального значения. Погрешность усиления - это величина, на которую G отличается от идеального значения. В общем случае, погрешность усиления может быть выражена разностью двух коэффициентов, выраженной в процентах. Эту разность можно рассматривать, как вклад погрешности усиления (в мВ или значениях младшего разряда LSB) в общую погрешность при максимальном значении сигнала. Обычно пользователю предоставляется возможность минимизации этих погрешностей. Обратите внимание, что, в усилителе сначала регулируют смещение при нулевом входном сигнале, а затем настраивают коэффициент усиления при значении входного сигнала, близком к максимальному. Алгоритм настройки биполярных преобразователей более сложен.

Рисунок 3. ПОГРЕШНОСТЬ СМЕЩЕНИЯ НУЛЯ ПРЕОБРАЗОВАТЕЛЯ И ПОГРЕШНОСТЬ УСИЛЕНИЯ
Интегральная нелинейность ЦАП и АЦП аналогична нелинейности усилителя и определяется как максимальное отклонение фактической характеристики передачи преобразователя от прямой линии. В общем случае, она выражается в процентах от полной шкалы (но может представляться в значениях младших разрядов). Существует два общих метода аппроксимации характеристики передачи: метод конечных точек (end point) и метод наилучшей прямой (best straight line) (см. рисунок 4).

Рисунок 4. МЕТОД ИЗМЕРЕНИЯ СУММАРНОЙ ПОГРЕШНОСТИ ЛИНЕЙНОСТИ
При использовании метода конечных точек измеряется отклонение произвольной точки характеристики (после коррекции усиления) от прямой, проведенной из начала координат. Таким образом в компании Analog Devices, Inc. измеряют значения интегральной нелинейности преобразователей, используемых в задачах измерения и управления (так как величина погрешности зависит от отклонения от идеальной характеристики, а не от произвольного "наилучшего приближения").
Метод наилучшей прямой дает более адекватный прогноз искажений в приложениях, имеющих дело с сигналами переменного тока.
Он менее чувствителен к нелинейностям технических характеристик. По методу наилучшего приближения через характеристику передачи устройства проводят прямую линию, используя стандартные методы интерполяции кривой. После этого максимальное отклонение измеряется от построенной прямой. Как правило, интегральная нелинейность, измеренная таким образом, учитывает только 50% нелинейности, оцененной методом конечных точек. Это делает метод предпочтительным при указании впечатляющих технических характеристик в спецификации, но менее полезным для анализа реальных значений погрешностей. Для приложений, имеющих дело с сигналами переменного тока, лучше определять гармонические искажения, чем нелинейность по постоянному току, так что для определения нелинейности преобразователя необходимость в использовании метода наилучшей прямой возникает довольно редко.
Другой тип нелинейности преобразователей - дифференциальная нелинейность (DNL). Она связана с нелинейностью кодовых переходов преобразователя. В идеальном случае изменение на единицу младшего разряда цифрового кода точно соответствует изменению аналогового сигнала на величину единицы младшего разряда. В ЦАП изменение одного младшего разряда цифрового кода должно вызывать изменение сигнала на аналоговом выходе, в точности соответствующее величине младшего разряда. В то же время в АЦП при переходе с одного цифрового уровня на следующий значение сигнала на аналоговом входе должно измениться точно на величину, соответствующую младшему разряду цифровой шкалы.
Там, где изменение аналогового сигнала, соответствующее изменению единицы младшего разряда цифрового кода, больше или меньше этой величины, говорят об дифференциальной нелинейной (DNL) погрешности. DNL-погрешность преобразователя обычно определяется как максимальное значение дифференциальной нелинейности, выявляемое на любом переходе.
Если дифференциальная нелинейность ЦАП меньше, чем –1 LSB на любом переходе (см. рис.2.12), ЦАП называют немонотонным, и его характеристика передачи содержит один или несколько локальных максимумов или минимумов.
Дифференциальная нелинейность, большая чем + 1 LSB, не вызывает нарушения монотонности, но также нежелательна. Во многих приложениях ЦАП (особенно в системах с обратной связью, где немонотонность может изменить отрицательную обратную связь на положительную) монотонность ЦАП очень важна. Часто монотонность ЦАП явно оговаривается в техническом описании, хотя, если дифференциальная нелинейность гарантированно меньше единицы младшего разряда (то есть, |DNL| . 1LSB), устройство будет обладать монотонностью, даже если это явно не указывается.
Бывает, что АЦП немонотонен, но наиболее распространенным проявлением DNL в АЦП являются пропущенные коды. (см. рис.2.13). Пропущенные коды (или немонотонность) в АЦП столь же нежелательны, как немонотонность в ЦАП. Опять таки, это возникает при DNL > 1 LSB.

Рис. 2.12 Функция передачи неидеального 3-разрядного ЦАП

Рис. 2.13 Функция передачи неидеального 3-разрядного ЦАП
Определение отсутствующих кодов сложнее, чем определение немонотонности. Все АЦП характеризуются некоторым шумом перехода (transition noise), иллюстрируемым на рис.2.14 (представьте себе этот шум как мелькание последней цифры цифрового вольтметра между соседними значениями). По мере роста разрешающей способности диапазон входного сигнала, соответствующий уровню шума перехода, может достичь или даже превысить значение сигнала, соответствующее единице младшего разряда. В таком случае, особенно в сочетании с отрицательной DNL- погрешностью, может случиться так, что появятся некоторые (или даже все) коды, где шум перехода будет присутствовать во всем диапазоне значений входных сигналов. Таким образом, возможно существование некоторых кодов, для которых не существует значения входного сигнала, при котором этот код гарантированно бы появился на выходе, хотя и может существовать некоторый диапазон входного сигнала, при котором иногда будет появляться этот код.

Рис. 2.14 Совместное действие шумов перехода кода и дифференциальной нелинейности (DNL)
Для АЦП с невысокой разрешающей способностью можно определить условие отсутствия пропущенных кодов как сочетание шума перехода и дифференциальной нелинейности, при котором гарантировался бы некоторый уровень (скажем, 0.2 LSB) свободного от шума кода для всех кодов.Однако при этом невозможно достичь столь высокой разрешающей способности, которую обеспечивают современные сигма-дельта АЦП, или даже меньшей разрешающей способности для АЦП с широкой полосой пропускания. В этих случаях производитель должен определять уровни шумов и разрешающую способность каким-нибудь другим способом. Не так важно, какой метод используется, но спецификация должна содержать четкое определение используемого метода и ожидаемые характеристики.
Структурная схема цифрового устройства обработки сигнала
Структурная схема устройства ЦОС представлена на рис. 2.1. По теореме Котельникова предполагается, что сигнал на входе АЦП ограничен по частоте. Однако реальные сигналы обладают спектром, распространяющимся до бесконечности. Поэтому, прежде чем подвергнуться аналого-цифровому преобразованию, непрерывный сигнал проходит через схему аналоговой обработки, которая выполняет такие функции, как усиление (или ослабление) и фильтрация. Для подавления мешающих сигналов за пределами интересующей полосы частот и предотвращения наложения спектров при дискретизации аналогового сигнала необходим фильтр низкой частоты или полосовой фильтр.

Рисунок 1. Структурная схема цифрового устройства
На рисунке 1 представлена система, работающая в реальном масштабе времени. В ней устройство выборки и хранения (дискретизатор) непрерывно стробирует сигнал с частотой, равной fs, и АЦП выдает новый отсчет сигнала процессору ЦОС (DSP). Для обеспечения работы в реальном масштабе времени сигнальный процессор должен закончить все вычисления в пределах интервала дискретизации 1/fs и передать выходной отсчет на ЦАП до поступления следующего отсчета с АЦП. В качестве примера устройства цифровой обработки сигнала может выступать цифровой фильтр.
Возможна другая реализация устройств реального времени. При реализации на сигнальном процессоре алгоритма БПФ, входной блок данных целиком загружается в память этого процессора. Для обеспечения работы устройства в реальном масштабе времени пока сигнальный процессор выполняет алгоритм БПФ над ранее полученным блоком данных, новый блок данных накапливается в памяти. Сигнальный процессор должен успеть вычислить спектр в течение интервала накопления блока данных, чтобы быть готовым к процессу обработки следующего блока данных.
Обратите внимание, что ЦАП требуется только в том случае, когда данные необходимо преобразовать обратно в аналоговый сигнал (например, при обработке изображения или звука). Есть много устройств, где после первоначального аналого-цифрового преобразования сигнал остается в цифровом формате. Кроме того существуют устройства в которых сигнальный процессор предназначен исключительно для формирования сигнала, подаваемого на ЦАП такие как CD-проигрыватели. Если в устройстве используется ЦАП, то на его выходе для подавления нежелательных составляющих выходного спектра необходимо применять формирующий фильтр (anti-imaging filter).
В реальных процессах аналого-цифрового и цифро-аналогового преобразования есть два ключевых этапа: дискретизация (квантование по времени) и квантование по амплитуде, которые определяют разрешающую способность данных операций. Понимание этих моментов является основополагающим фактором в оценке приложений ЦОС.
Субдискретизация (дискретизация
До сих пор мы рассматривали случай дискретизации низкочастотных сигналов (видеосигналов или огибающих), когда все интересующие нас сигналы лежат в первой зоне Найквиста. На рис.2.6 A представлен случай, когда полоса оцифрованных сигналов ограничена первой зоной Найквиста, а в остальных зонах Найквиста появляются образы первоначального диапазона частот.

Рис. 2.6 Субдискретизация сигнала
Рассмотрим случай, показанный на рис.2.6 B, где полоса дискретизированного сигнала полностью находится во второй зоне Найквиста. Часто процесс дискретизации сигнала, находящегося вне первой зоны Найквиста, называется субдискретизацией или дискретизацией гармонического сигнала. Отметим, что образ сигнала в первой зоне Найквиста содержит всю информацию об исходном сигнале, за исключением его первоначального местоположения (кроме того порядок частот в спектре обратный, но это легко корректируется переупорядочиванием компонентов спектра на выходе БПФ).
На рис.2.6 C показан вариант дискретизированного сигнала, расположенного в третьей зоне Найквиста. Отметим, что в первой зоне Найквиста нет обращения частот. Действительно, частоты подлежащих дискретизации сигналов могут лежать в любой зоне Найквиста, и боковая полоса в первой зоне Найквиста является точным представлением сигнала (за исключением обращения частот, которое происходит, когда сигналы расположены в четных зонах Найквиста). Здесь мы можем вновь ясно сформулировать критерий Найквиста:
Сигнал должен быть дискретизирован со скоростью равной или большей удвоенной полосы частот для того, чтобы сохранить всю информацию о сигнале.
Обратите внимание, что в этой формулировке нет никакого упоминания об абсолютном местоположении полосы дискретизируемых сигналов в частотном спектре относительно частоты дискретизации. Единственное ограничение состоит в том, что полоса подлежащих дискретизации сигналов ограничена одной зоной Найквиста, то есть, полосы сигналов не должны перекрывать частоту fs/2 с любым множителем (это на самом деле и является основной функцией антиалайзингового фильтра).
Дискретизация сигналов, лежащих выше первой зоны Найквиста, стала популярной в аппаратуре связи так как этот процесс эквивалентен аналоговой демодуляции. Обычным становится дискретизация сигналов ПЧ с последующим использованием цифровых методов для обработки сигнала. таким способом исчезает необходимость использования демодулятора ПЧ. Ясно, что с ростом ПЧ растут и требования к производительности АЦП. Ширина полосы входа АЦП и характеристики, связанные с допустимыми искажениями сигналов, должны быть адекватны скорее ПЧ, чем основной полосе частот. Это является проблемой для большинства АЦП, предназначенных для обработки сигналов в первой зоне Найквиста, поэтому для субдискретизации нужен АЦП, который может обрабатывать сигналы в других более высокочастотных зонах Найквиста.
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
Контрольная работа посвящена изучению архитектуры, системы команд, методов программирования и использования в технике связи микроконтроллеров семейства MCS-51.
При решении заданий контрольной работы и подготовке к ее защите необходимо учесть, что общие вопросы построения микропроцессорных систем изложены в [9]. Конкретные примеры построения контроллеров на основе однокристальных ЭВМ этого семейства подробно изложены в - [4]. Поэтому рекомендуется перед выполнением контрольной работы сначала ознакомиться с содержанием учебников, а затем подробно изучить вопросы построения микроконтроллеров на основе микро-ЭВМ MCS-51.
Контрольная работа состоит из двух заданий. В каждом задании номер варианта определяется по двум последним цифрам шифра студента, через i обозначена последняя, через j – предпоследняя цифра шифра студента.
Задание 1. Записать результат выполнения команд ОЭВМ семейства MCS-51, приведенных в таблице 5, указать источник, приемник и способы используемой адресации для каждого из операндов. При выполнении задания обязательно записывать содержимое регистров микроконтроллера до выполнения команды и содержимое регистров микроконтроллера после выполнения команды.
Таблица 1 Исходные данные к заданию 1
| 1 | MOV A, ij; (A)=2iH, (внутр. ОЗУ [ijH])=i, (PC)=1jiH | |
| 2 | MOVX A, @DPTR; (A)=2iH, (DPTR)=0i0jH, (внешн. ОЗУ [0i0jH])=jiH, (PC)=2jiH | |
| 3 | MOVC A, @A+DPTR; (A)=2iH, (DPTR)=0i0jH, (содержимое операнда-источника из ПЗУ)=jiH, (PC)=2jiH | Указать адрес операнда-источника в ПЗУ |
| 4 | ADD A, @R0; (A)=1iH, (R0)=ijH, (внутр. ОЗУ [ijH])=i, (PC)=1jiH | |
| 5 | ANL P1, #ijH; (P1)=jiH, (PC)=1jiH | |
| 6 | ORL P1, #ijH; (P1)=jiH, (PC)=1jiH | |
| 7 | SETB P1.3; (P1)=jiH, (PC)=1jiH | |
| 8 | LJMP ijH, (PC)=4jiH | |
| 9 | LABLE: JB P1.3, LABLE;;(P1)=jiH, (pc)=1jiH | |
| 10 | LABLE: JNB P1.3, LABLE;;(P1)=jiH, (pc)=1jiH |
Задание 2. Написать фрагмент программ, обеспечивающий выполнение действий в соответствии с таблицей 6.
При написании программы обязательно использование комментариев, поясняющих действие каждой группы команд. К каждой программе обязательно должна прилагаться принципиальная схема контроллера, соответствующая заданию.
Таблица 2 Исходные данные к заданию 2
| Номер варианта | Задание 2.1. | Задание 2.2. |
| j1 | Обнуление всех ячеек внутренней памяти данных | Генерация меандра на выводе P1.0 с частотой 50кГц (период 20мкс). |
| j2 | Сложение двух 16-разрядных чисел. 1-е слагаемое: мл. байт расположен по адресу 14Н; ст. байт - 15Н; 2-е слагаемое: мл. байт расположен по адресу 12Н; ст. байт - 13Н | Включение привода и опрос концевого датчика  |
| j3 | Вывод символа «6» при подключении к микроконтроллеру светодиодного индикатора АЛС324Б. | Запуск трёхфазного двигателя при нажатии кнопки S  |
| j4 | Сложение 16-разрядного и 8-разрядного чисел. 1-е слагаемое: мл. байт (А)=11Н; ст. байт (R2)=23Н; 2-е слагаемое: (R3)=14Н | Программно реализованная временная задержка на 1 мс |
| j5 | Деление массива чисел, хранящихся во внутреннем ОЗУ (ячейки 24Н … 33Н) на 4 | Сохранение регистров текущего банка в стеке |
| j6 | Сложение двух двоично-десятичных чисел в упакованном формате. 1-е слагаемое: мл. байт расположен по адресу 14Н; ст. байт - 16Н; 2-е слагаемое: мл. байт расположен по адресу 11Н; ст. байт - 13Н | Реализовать временную задержку на 1 мс на таймере T0. |
| j7 | Сложение ячеек 33h …70h внутренней памяти данных с константой, равной 2 | Вывод символа «3» при подключении к микроконтроллеру светодиодного индикатора АЛС314Б. |
| j8 | Генерация меандра на выводе P1.4 с частотой 20 кГц (период 50 мкс) | Переход к выполению подпрограммы при срабатывании концевого датчика (замыкание ключа S)  |
| j9 | Пересылка данных из внутреннего во внешнее ОЗУ ОЭВМ с теми же адресами | Вызов подпрограммы CNT с приходом 56-го импульса на входе Т0 микроконтроллера |
| j0 | Подключение 8-кнопочной клавиатуры к микроконтроллеру (схема, программа) | Обнуление всех ячеек внешней памяти данных |
>
А Фрунзе
Перед тем как издать книгу, опубликовал ряд статей в журнале схемотехника по этой же тематике. Прекрасное сочетание схем и программ для них! Некоторые из них доступны в электронном виде:
(pdf 160 кбайт) (pdf 360 кбайт) (pdf 500 кбайт) (pdf 83 кбайт) (pdf 101 кбайт) (pdf 256 кбайт) (pdf 346 кбайт) (pdf 684 кбайт) (pdf 327 кбайт) Не знаю как у Фрунзе, а у меня, когда я после окончания института сочинил подобную схему, изображение пришлось смотреть только в полной темноте! Яркость светодиодов падает пропорционально скважности коммутирующих импульсов! Можно скомпенсировать увеличением импульсного тока через светодиод, но тогда необходимо умощнить дешифраторы. (pdf 952 кбайт) (pdf 135 кбайт) (продолжение) (pdf 54 кбайт)Для тех, кто желает проверить работу программ, приведённых в этих статьях можно скачать ассемблер , но лучше переделать программы под профессиональный свободно распространяемый ассемблер . Описание работы с этой программой можно найти , а техническое руководство находится непосредственно в zip архиве.
Analog Devices
Справочные материалы по микросхемам семейства MCS-51:
Микросхема прямого цифрового синтеза:
Atmel
Справочные материалы по микросхемам семейства MCS-51:
Справочные материалы по микросхемам семейства AVR:
- описание на русском языке, составленноеБ Уидроу
Достаточно часто цифровые устройства реализуют алгоритмы адаптивного приема сигналов. В данной книге одного из основоположников адаптивного приема подробно рассматриваются математические основы таких алгоритмов.
М. Радио и связь 1989 г.
[ ]
Джон Прокис
Пытаться построить устройство цифровой обработки сигналов не зная для чего предназначены эти сигналы достаточно проблематично. Современные системы цифровой связи строятся на основе глубоких знаний структуры передаваемых сигналов и помех этим сигналам. Это невозможно без теоретических основ радиотехники. Джон Прокис написал на мой взгляд наиболее полную и в то же самое время наиболее доступную для понимания книгу по теоретическим основам цифровой радиосвязи. Настоятельно советую изучить эту книгу. При этом желательно неоднократное возвращение к ней после некоторых перерывов, во время которых будут рассматриваться более простые вопросы и разрабатываться реальные устройства.
М. Радио и связь 2000 г.
Литература по преподаваемым дисциплинам
Некоторые книги записаны в формате DJVu. Программу просмотра книг в этом формате можно скачать .
ЛР Рабинер Б Гоулд
Теория и применение цифровой обработки сигналов
(продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение) (продолжение)ЛР Рабинер РВ Шафер
Цифровая обработка речевых сигналов
(продолжение) (продолжение) .Михаил Гук
По моему эти файлы, найденные в интернете, содержат информацию из книг Михаила Гука Аппаратные средства IBM PC и Периферийные устройства IBM PC, хотя прямых ссылок я не обнаружил.
Motorola
Справочные материалы по микросхемам семейства HC11:
Немного об истории
К сожалению мне не удалось прочитать большого количества книг по истории как нашего государства, так по истории других государств. Но даже того, что я прочитал хватило чтобы понять, что то что творится сейчас и даже то, что произойдёт в будущем уже было. Было если не в нашей истории, то в истории других государств. Проблемы, которые встают сейчас перед нами вставали и перед предыдущими поколениями людей. Решения этих проблем как это ни странно - стандартные! И одни приводят к немедленному краху государства (при этом обычно гибнут и люди, населяющие его), другие приводят к его процветанию. И тут развеялась ещё одна легенда - оказалось, что процветание государства не обязательно процветание народов, населяющих его! В общем я понял: история это не наука о прошлом - история это наука о будущем!
Наибольшее впечатление на меня произвела история государства российского Карамзина. Но только не урезанный вариант! Я видел и урезанный вариант этой книги - не то!
В библиотеке нашего университета есть книга с летописями освоения Сибири. Это тоже нечто! Читать советую на древнерусском языке - прочитав две страницы вы забудете, что это древнерусский язык. Зато исчезнут многие легенды, которыми нас потчуют учебники истории, а особенно телевизор! Наибольший шок у меня вызвало то, что у казаков, идущих на Сибирь не было превосходства в оружии! Сибирские народы были вооружены лучше! Одно то, что предводители казаков Ермак и Иван Кольцо были одеты в сибирские (а не русские) латы и вооружены сибирскими же саблями говорит о многом!
Успех их атаки объясняется другим - это была карательная экспедиция! Они выбивали среднеазиатского узурпатора! И сибирские народы поддерживали их! В общем лучше прочитать первоисточник самим!
Интересна и история освобождения Московии от власти татар. Наибольшие сведения я получил, прочитав Задонщину - летописное описание событий Куликовской битвы. И снова шок! Дмитрий Донской уменьшается и вдруг неизмеримо вырастают фигуры Боброка, который за три года до Куликовской битвы при Воже уже разбил татарскую орду, большую по численности чем орда Мамая, и Сергия Радонежского, организовавшего успех этих битв.
В общем лучше почитать самим.
Мне удалось найти описание русской истории Соловьёва. Если у кого есть Карамзин или есть ссылка на сайт, где находятся его книги пришлите пожалуйста мне по адресу
Сергей Михайлович СОЛОВЬЕВ "ИСТОРИЯ РОССИИ С ДРЕВНЕЙШИХ ВРЕМЕН"
(rar-архив 160кбайт)
(rar-архив 230кбайт)
(rar-архив 220кбайт)
(rar-архив 220кбайт)
(rar-архив 250кбайт)
(rar-архив 240кбайт)
(rar-архив 240кбайт)
(rar-архив 250кбайт)
[ ]
Ричард Блейхут
На мой взгляд это самые лучшие книги по алгоритмам быстрой обработки сигналов и кодированию из тех, что я видел
(К сожалению в приложениях, содержатся ошибки)С Л Марпл-мл
Книга посвящена спектральному анализу коротких выборок данных. Рассмотренные методы альтернативны методам быстрого преобразования Фурье. Очень полезна для анализа непериодических коротких сигналов
С. Л. Марпл-мл., Москва: Мир, 1990.
Уолт Кестер
По моему это одна из лучших книг по цифровой обработке сигналов
(pdf 330 кбайт) (pdf 920 кбайт) (pdf 740 кбайт) (pdf 490 кбайт) (pdf 690 кбайт) (pdf 880 кбайт) (pdf 150 кбайт) (pdf 560 кбайт) (pdf 1050 кбайт) (pdf 1300 кбайт)